library(tidyverse)
# remotes::install_github("joon-e/soscisurvey")
library(soscisurvey)
library(lme4)
library(marginaleffects)
theme_set(theme_minimal())9 Experimentaldaten auswerten
Wir beginnen damit, die für unsere Analyse notwendigen Pakete zu laden. Mit Hilfe des soscisurvey-Pakets können wir direkt die aktuellen Daten aus jedem Projekt importieren, die für API-Zugriff freigegeben sind. Für die Analyse benötigen wir noch das Paket lme4 und marginaleffects für Kontraste und Modellvorhersagen.
9.1 Daten laden und vorbereiten
9.1.1 Laden der Daten von der SosciSurvey-API
Als erstes laden wir die Umfragedaten mit der Funktion read_sosci(). Wir filtern die Daten anschließend , um nur die Antworten aus der Feldphase (nicht Pretest etc.) zu behalten. Dann behandeln wir fehlende Werte aus Soscisurvey, die meist als negative Werte codiert sind, mit mutate_if() und ersetzen sie durch korrekte NA.
d <- soscisurvey::read_sosci("https://sosci.zdv.uni-mainz.de/scharkow-exp1/?act=DZkRsYcp1cf2frs5VunopI4l") |>
filter(MODE == "interview") |>
mutate_if(is.numeric, ~ ifelse(. < 0, NA, .))
d# A tibble: 5 × 23
CASE QUESTNNR MODE STARTED IV01_01 LASTDATA FINISHED Q_VIEWER LASTPAGE
<int> <chr> <chr> <chr> <chr> <chr> <int> <int> <int>
1 24 base interview 2025-06-… 1 2025-06… 1 0 6
2 25 base interview 2025-06-… 4 2025-06… 1 0 6
3 26 base interview 2025-06-… 4 2025-06… 1 0 6
4 27 base interview 2025-06-… 1 2025-06… 1 0 6
5 28 base interview 2025-06-… 3 2025-06… 1 0 6
# ℹ 14 more variables: MAXPAGE <int>, TIME001 <int>, TIME_SUM <int>,
# TIME002 <int>, TIME003 <int>, F101_01 <int>, F101_02 <int>, F101_03 <int>,
# TIME004 <int>, F102_01 <int>, F102_02 <int>, F102_03 <int>, TIME005 <int>,
# TIME006 <int>Wir schauen uns dann alle Variablennamen im Datensatz an.
names(d) [1] "CASE" "QUESTNNR" "MODE" "STARTED" "IV01_01" "LASTDATA"
[7] "FINISHED" "Q_VIEWER" "LASTPAGE" "MAXPAGE" "TIME001" "TIME_SUM"
[13] "TIME002" "TIME003" "F101_01" "F101_02" "F101_03" "TIME004"
[19] "F102_01" "F102_02" "F102_03" "TIME005" "TIME006" 9.1.2 Within-Subject Daten ins Langformat konvertieren
Bei Between-Subject-Designs könnten wir nun unmittelbar mit der Auswertung beginnen, etwa mit einem T-Test wie t.test(outcome ~ gruppe). Da wir aber ein Within-Subject-Design verwenden, müssen wir die Daten in eine Form bringen, die für unsere weiteren Analysen besser geeignet ist. Wir wählen zunächst die benötigten Spalten mit select() aus und transformieren die Daten mit gather() von einem breiten in ein langes Format. Anschließend teilen wir die Spaltennamen mit separate() in “seite” und “item” auf, und extrahieren die letzte Ziffer der Seitenzahl mit mutate(). Zum Schluss nutzen wir spread(), um die Daten wieder in ein breites Format zu bringen, wobei jedes Item eine eigene Spalte erhält.
d_lang <- d |>
select(CASE, gruppe = IV01_01, starts_with("F1")) |>
gather(variable, wert, -CASE, -gruppe) |>
separate(variable, into = c("seite", "item")) |>
mutate(seite = str_sub(seite, -1, -1)) |>
spread(item, wert, sep = "_")
d_lang# A tibble: 10 × 6
CASE gruppe seite item_01 item_02 item_03
<int> <chr> <chr> <int> <int> <int>
1 24 1 1 3 4 4
2 24 1 2 5 5 2
3 25 4 1 1 3 1
4 25 4 2 3 2 1
5 26 4 1 2 1 2
# ℹ 5 more rowsDer finale Datensatz hat eine Zeile für jede Kombination von Versuchsperson und Stimulus, sowie alle dazugehörigen Messungen als separate Spalten. Dies ermöglicht es uns, ganz einfach die verschiedenen Versuchsbedingungen als separate Datei hinzuzufügen.
9.1.3 Versuchsplan laden und Daten zusammenführen
Als nächstes laden wir den Versuchsplan aus einer TSV-Datei mit read_tsv() und betrachten diesen kurz. Wir sehen, es wird für jede Gruppe definiert, in welcher Variante welcher Stimulus gezeigt wird. Hier haben wir es mit einem 2x2 Design mit den Faktoren ki_ursprung und ki_markierung zu tun, wobei alle Kombinationen den Gruppen in unterschiedlicher Reihenfolge dargeboten werden.
versuchsplan <- read_tsv("data/versuchsplan.tsv", col_types = "cccc")
versuchsplan# A tibble: 16 × 4
gruppe seite ki_ursprung ki_markierung
<chr> <chr> <chr> <chr>
1 1 1 1 1
2 1 2 1 0
3 1 3 0 1
4 1 4 0 0
5 2 1 0 0
# ℹ 11 more rowsUm die experimentellen Bedingungen in unserer Analyse zu berücksichtigen, führen wir den Versuchsplan mit den Befragungsdaten mithilfe von left_join() zusammen. Die gemeinsame Variable sind hier gruppe und seite, d.h. diese beiden müssen exakt in beiden Datensätzen vorkommen.
d_lang <- d_lang |>
left_join(versuchsplan, by = c("gruppe", "seite"))
d_lang# A tibble: 10 × 8
CASE gruppe seite item_01 item_02 item_03 ki_ursprung ki_markierung
<int> <chr> <chr> <int> <int> <int> <chr> <chr>
1 24 1 1 3 4 4 1 1
2 24 1 2 5 5 2 1 0
3 25 4 1 1 3 1 0 1
4 25 4 2 3 2 1 1 0
5 26 4 1 2 1 2 0 1
# ℹ 5 more rowsFür jede Versuchsperson (CASE) ist nun klar, welchen Stimulus sie wann in welcher Variante gesehen hat. Dies funktioniert auch mit weniger oder mehr Faktoren, solange diese im Versuchsplan als Spalten angelegt sind.
9.2 Daten auswerten
9.2.1 Mittelwertindex berechnen
Typischerweise verwenden wir mehr als ein Item für unsere Outcome-Variablen. Daher berechnen wir nun beispielhaft einen Gesamtscore overall für jeden Teilnehmer, indem wir den Mittelwert der Antworten auf die Items item_01, item_02 und item_03 mit rowMeans() berechnen. Dies ginge natürlich auch mit mehr Items und/oder mehreren Outcome-Indices.
d_lang <- d_lang |>
mutate(overall = rowMeans(select(d_lang, item_01, item_02, item_03), na.rm = TRUE))
d_lang# A tibble: 10 × 9
CASE gruppe seite item_01 item_02 item_03 ki_ursprung ki_markierung overall
<int> <chr> <chr> <int> <int> <int> <chr> <chr> <dbl>
1 24 1 1 3 4 4 1 1 3.67
2 24 1 2 5 5 2 1 0 4
3 25 4 1 1 3 1 0 1 1.67
4 25 4 2 3 2 1 1 0 2
5 26 4 1 2 1 2 0 1 1.67
# ℹ 5 more rows9.2.2 Deskriptive Statistik
Bevor wir mit der Modellierung beginnen, betrachten wir einige deskriptive Statistiken. Wir gruppieren die Daten nach ki_ursprung mit group_by() und berechnen dann für jede Gruppe den Mittelwert (mean) und die Standardabweichung (sd) des Gesamtscores overall mit summarise()
d_lang |>
group_by(ki_ursprung) |>
summarise(
m = mean(overall, na.rm = TRUE),
sd = sd(overall, na.rm = TRUE)
)# A tibble: 2 × 3
ki_ursprung m sd
<chr> <dbl> <dbl>
1 0 1.61 0.0962
2 1 3.57 1.24 9.2.3 Multilevel-Modellierung
Jetzt können wir mit der eigentlichen statistischen Modellierung beginnen. Wir verwenden lmer() um ein Mixed-Effects-Modell zu schätzen, da wir ja Messwiederholungen pro Versuchsperson haben. Mit icc() berechnen wir den Intraclass-Korrelationskoeffizienten, um zu beurteilen, wie stark die Unterschiede zwischen den Personen sind.
lmer(overall ~ 1 + (1 | CASE), data = d_lang) |>
performance::icc()[1] NANun schätzen wir unser eigentliches Modell, um die experimentellen Variablen ki_ursprung und ki_markierung sowie deren Interaktion zu berücksichtigen. Da eine Interaktion zwischen den Faktoren geschätzt wurde, sind alle einzelnen Regressionskoeffizienten konditional, d.h. keine klassischen Haupteffekte.
m1 <- lmer(overall ~ ki_ursprung * ki_markierung + (1 | CASE), data = d_lang)
report::report_table(m1)Random effect variances not available. Returned R2 does not account for random effects.Parameter | Coefficient | 95% CI | t(4)
------------------------------------------------------------------------
(Intercept) | 1.50 | [-1.85, 4.85] | 1.24
ki ursprung [1] | 1.90 | [-1.77, 5.57] | 1.44
ki markierung [1] | 0.17 | [-3.94, 4.27] | 0.11
ki ursprung [1] × ki markierung [1] | 0.43 | [-4.54, 5.41] | 0.24
| 1.49e-10 | |
| 1.21 | |
| | |
AIC | | |
AICc | | |
BIC | | |
R2 (marginal) | | |
Sigma | | |
Parameter | p | Effects | Group | Std. Coef.
-----------------------------------------------------------------------------
(Intercept) | 0.282 | fixed | | -1.07
ki ursprung [1] | 0.224 | fixed | | 1.37
ki markierung [1] | 0.916 | fixed | | 0.12
ki ursprung [1] × ki markierung [1] | 0.821 | fixed | | 0.31
| | random | CASE |
| | random | Residual |
| | | |
AIC | | | |
AICc | | | |
BIC | | | |
R2 (marginal) | | | |
Sigma | | | |
Parameter | Std. Coef. 95% CI | Fit
---------------------------------------------------------------
(Intercept) | [-3.48, 1.35] |
ki ursprung [1] | [-1.28, 4.01] |
ki markierung [1] | [-2.84, 3.08] |
ki ursprung [1] × ki markierung [1] | [-3.27, 3.89] |
| |
| |
| |
AIC | | 34.29
AICc | | 62.29
BIC | | 36.11
R2 (marginal) | | 0.40
Sigma | | 1.219.2.4 Kontraste und Vorhersagen
Die eigentlichen Haupteffekte erhalten wir, indem wir gezielt die Effekte der beiden Experimentalfaktoren betrachten. Dies geht am einfachsten mit der Funktion avg_comparisons() aus dem marginaleffects-Paket. Für Multilevel-Modelle sollten wir nur die sog. fixed effects betrachten, daher der zusätzliche Parameter re.form = NA.
marginaleffects::avg_comparisons(m1, re.form = NA)
Term Estimate Std. Error z Pr(>|z|) S 2.5 % 97.5 %
ki_markierung 0.47 0.835 0.563 0.5736 0.8 -1.167 2.11
ki_ursprung 2.07 0.929 2.231 0.0257 5.3 0.252 3.90
Type: response
Comparison: 1 - 0Zum Schluss wollen wir die Effekte unserer Variablen besser verstehen. Wir berechnen die durchschnittlichen Vorhersagen pro Bedingung mit avg_predictions() aus dem marginaleffects-Paket. Um die Ergebnisse anschaulich darzustellen, erstellen wir ein Diagramm, das die Vorhersagen für verschiedene Ausprägungen von ki_markierung und ki_ursprung zeigt, inklusive der dazugehörigen Konfidenzintervalle.
marginaleffects::avg_predictions(m1, variables = c("ki_ursprung", "ki_markierung"), re.form = NA) |>
ggplot(aes(
x = ki_markierung, y = estimate,
ymin = conf.low, ymax = conf.high,
color = ki_ursprung
)) +
geom_pointrange(position = position_dodge(.5))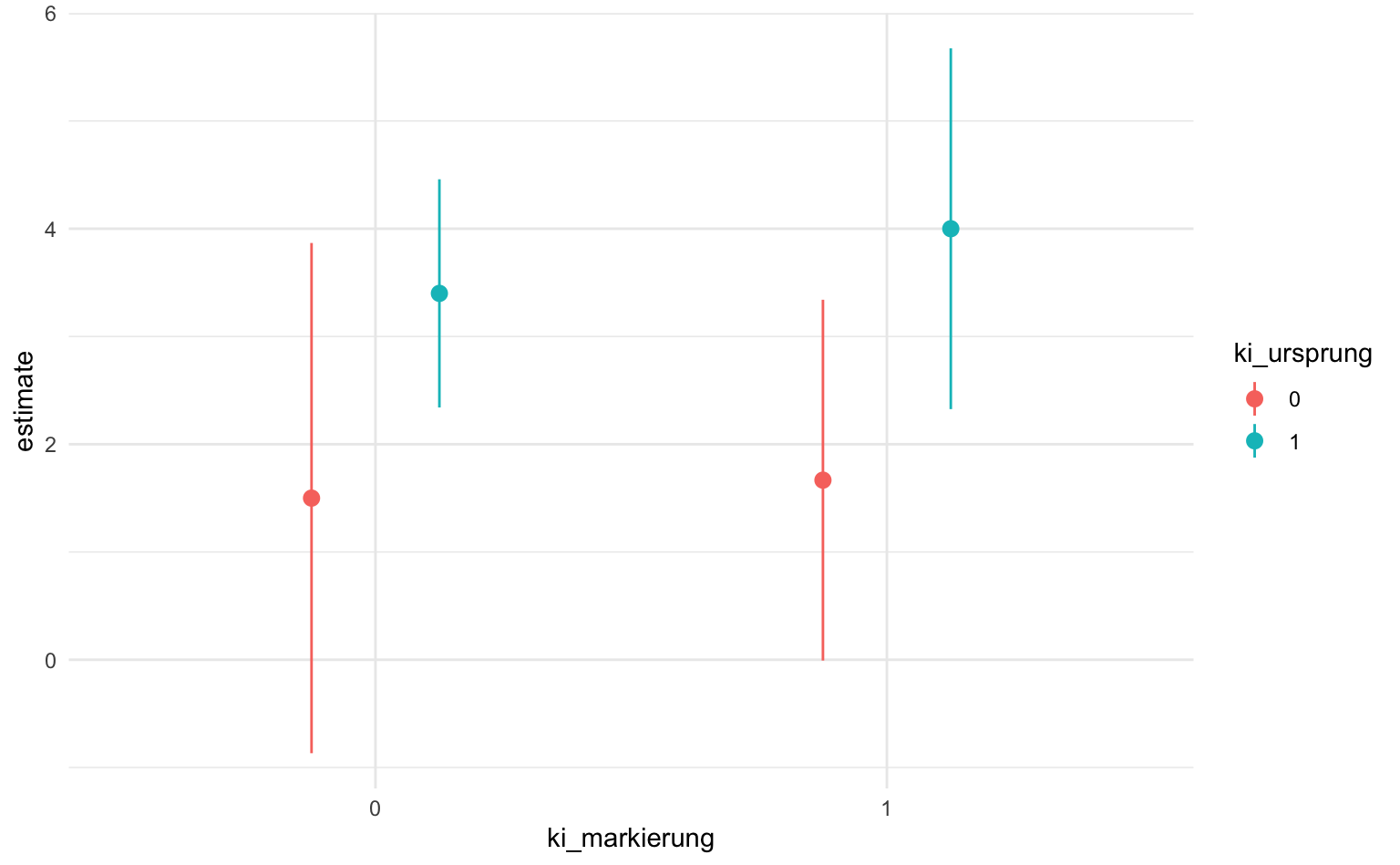
Hausaufgabe
Laden Sie Testdaten aus Ihrem eigenen Projekt per API und erstellen Sie eine minimale, korrekte Analyse damit. Sie können dafür beliebige Variablen verwenden.