library(tidyverse)
theme_set(theme_bw())
library(faux)
library(lme4)
library(tidyllm)5 Simulation
Wir laden wie immer das Paket tidyverse sowie für die Monte-Carlo-Simulation faux und Auswertung lme4. Für die generativen Agentenmodelle verwenden wir das tidyllm-Paket für die Interaktion mit verschiedenen Large Language Models.
5.1 Studiendaten simulieren
Bei der Planung von Experimenten und anderen empirischen Studien ist es oft hilfreich, künstliche Daten zu genieren, um zu prüfen, ob die Annahmen, das Design und die statistische Auswertung sinnvoll sind. Man unterscheidet dabei in stochastische Ansätze (Monte-Carlo-Simulation) und agentenbasierte Modelle. Wir starten zunächst mit der direkten Simulation von numerischen Daten.
5.1.1 Einfaches Between-Design
Der folgende Code simuliert Daten für ein einfaches Between-Subjects-Experiment. Die unabhängige Variable ad_type hat zwei Ausprägungen (“funny” und “not funny”). Die Funktion sim_design() aus dem Paket faux generiert die normalverteilte Daten, wobei die Mittelwerte (mu) für die beiden Gruppen unterschiedlich sind (2 bzw. 3), die Standardabweichung 1 ist und die Stichprobengröße pro Gruppe n=50 beträgt. Das Ergebnis wird in einem Tibble (df_between) gespeichert, gleichzeitig wird noch ein Plot erstellt.
between_factor <- list(ad_type = c("funny", "not funny"))
df_between <- sim_design(between = between_factor, mu = c(3, 2), sd = 1, n = 50) |>
as_tibble()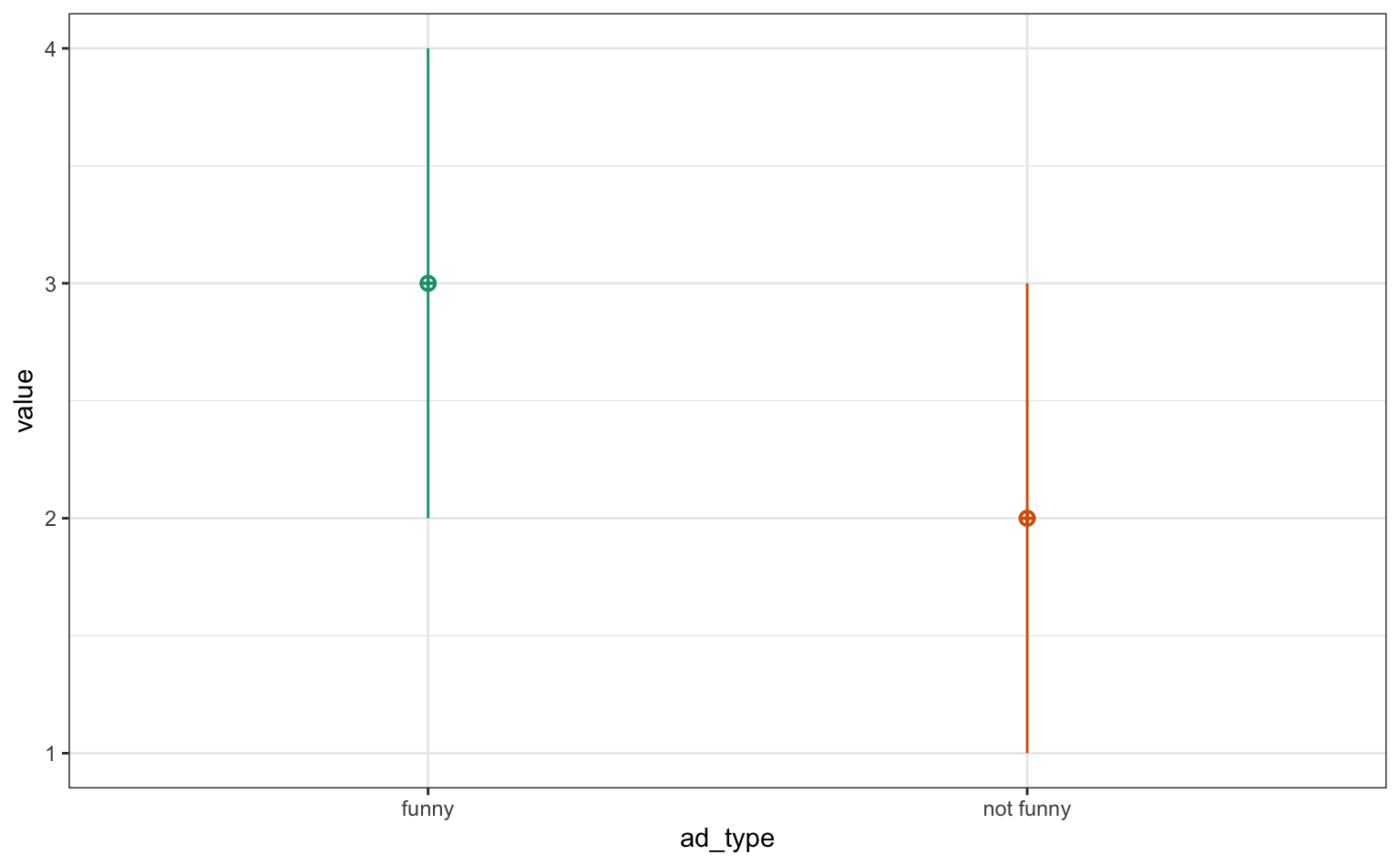
df_between# A tibble: 100 × 3
id ad_type y
<chr> <fct> <dbl>
1 S001 funny 2.46
2 S002 funny 4.21
3 S003 funny 2.71
4 S004 funny 4.75
5 S005 funny 2.98
# ℹ 95 more rowsJede Zeile repräsentiert eine Versuchsperson, und die Spalten enthalten die Ausprägung der unabhängigen Variable (ad_type) und die abhängige Variable (y). Wir vergleichen die simulierten Gruppenmittelwerte und SD, die grob den Input-Daten entsprechen:
df_between |>
group_by(ad_type) |>
summarise(m_y = mean(y), sd_y = sd(y))# A tibble: 2 × 3
ad_type m_y sd_y
<fct> <dbl> <dbl>
1 funny 2.92 1.13
2 not funny 2.19 0.809Nun wollen wir mit einem t-Test prüfen, ob es in den simulierten Daten einen signifikanten Unterschied zwischen den beiden Gruppen der unabhängigen Variable gibt. Die Funktion report_table() aus dem report-Paket formatiert die Ergebnisse des T-Tests in einer übersichtlichen Tabelle.
t.test(y ~ ad_type, data = df_between) |>
report::report_table()Welch Two Sample t-test
Parameter | Group | Mean_Group1 | Mean_Group2 | Difference | 95% CI | t(88.81) | p | d | d CI
---------------------------------------------------------------------------------------------------------------------
y | ad_type | 2.92 | 2.19 | 0.72 | [0.33, 1.11] | 3.68 | < .001 | 0.78 | [0.35, 1.21]
Alternative hypothesis: two.sidedWenig überraschend reproduziert der t-Test unsere simulierten Mittelwertunterschiede in der Grundgesamtheit.
5.1.2 Komplexere Designs
Nun erweitern die Simulation auf komplexere experimentelle Designs mit mehreren unabhängigen Variablen (Between- und Within-Subjects-Faktoren). Der folgende Code simuliert Daten für ein gemischtes Design. Es gibt eine Between-Subjects-Variable (age mit den Ausprägungen “young” und “old”) und zwei Within-Subjects-Variablen (ad_type mit “funny” und “not funny” sowie brand mit “bmw” und “mercedes”). Praktisch entspricht das einem Experiment, in dem jeder Versuchsperson vier Anzeigen gezeigt werden.
Die Funktion sim_design() generiert die Daten im Long-Format (long = TRUE), wobei r die Korrelation zwischen den Messwiederholungen (ICC) und n die Anzahl der Versuchspersonen angibt.
between_factors <- list(age = c("young", "old"))
within_factors <- list(
ad_type = c("funny", "not funny"),
brand = c("bmw", "mercedes")
)
df_mixed <- sim_design(
within = within_factors,
between = between_factors,
mu = 3, sd = 1, r = .5, n = 50,
long = TRUE, plot = FALSE
) |> as_tibble()Bislang gibt es keine Unterschiede zwischen den Anzeigen (mu ist identisch für alle). Daher erstellen wir jetzt nach unseren theoretischen Überlegungen eine neue Variable y_h1, die einen simulierten Effekt der unabhängigen Variablen enthält. Ältere Personen erhalten einen zusätzlichen Wert von 0.1, und witzige Anzeigen erhalten einen zusätzlichen Effekt von 0.3. Dies simuliert einen Haupteffekt dieser Variablen auf die abhängige Variable.
df_mixed <- df_mixed |>
mutate(y_h1 = (age == "old") * .1 + (ad_type == "funny") * .3 + y)
df_mixed |>
arrange(id)# A tibble: 400 × 6
id age ad_type brand y y_h1
<chr> <fct> <fct> <fct> <dbl> <dbl>
1 S001 young funny bmw 3.34 3.64
2 S001 young funny mercedes 4.27 4.57
3 S001 young not funny bmw 2.69 2.69
4 S001 young not funny mercedes 3.37 3.37
5 S002 young funny bmw 3.41 3.71
# ℹ 395 more rowsMit der Funktion lmer() aus dem lme4-Paket wird ein lineares gemischtes Modell geschätzt, das für dieses Experimentaldesign angemessen ist. Das Modell untersucht den Effekt von ad_type, wobei die Variabilität zwischen den Personen als varying intercept und slope (1 + ad_type | id) berücksichtigt wird.
lmer(y_h1 ~ ad_type + (1 + ad_type | id), data = df_mixed) |>
report::report_table()Parameter | Coefficient | 95% CI | t(394) | p | Effects | Group | Std. Coef. | Std. Coef. 95% CI | Fit
------------------------------------------------------------------------------------------------------------------------------------
(Intercept) | 3.40 | [ 3.24, 3.56] | 41.66 | < .001 | fixed | | 0.12 | [-0.05, 0.29] |
ad type [not funny] | -0.23 | [-0.38, -0.08] | -3.08 | 0.002 | fixed | | -0.25 | [-0.41, -0.09] |
| 0.65 | | | | random | id | | |
| 0.30 | | | | random | id | | |
| -0.40 | | | | random | id | | |
| 0.69 | | | | random | Residual | | |
| | | | | | | | |
AIC | | | | | | | | | 1015.90
AICc | | | | | | | | | 1016.11
BIC | | | | | | | | | 1039.85
R2 (conditional) | | | | | | | | | 0.46
R2 (marginal) | | | | | | | | | 0.02
Sigma | | | | | | | | | 0.69Wir finden auch hier den spezifizierten Effekt der Anzeigenart - witzige Anzeigen werden besser bewertet.
5.1.3 Statistische Power
Eine kleine Analyse demonstriert, wie die statistische Power (die Wahrscheinlichkeit, einen tatsächlichen Effekt zu finden) durch die Stichprobengröße beeinflusst wird. Hierzu wird ein neuer Datensatz df_mixed_n20 erstellt, der nur eine zufällige Stichprobe von 20 Personen (id) aus dem ursprünglichen Datensatz enthält. Dies reduziert die Stichprobengröße erheblich.
df_mixed_n20 <- df_mixed |>
filter(id %in% sample(unique(id), 20))
df_mixed_n20# A tibble: 80 × 6
id age ad_type brand y y_h1
<chr> <fct> <fct> <fct> <dbl> <dbl>
1 S007 young funny bmw 2.52 2.82
2 S009 young funny bmw 2.86 3.16
3 S014 young funny bmw 2.57 2.87
4 S025 young funny bmw 2.61 2.91
5 S026 young funny bmw 1.88 2.18
# ℹ 75 more rowsDas gleiche Modell wie zuvor wird nun mit dem reduzierten Datensatz geschätzt. Ein Vergleich der Ergebnisse mit denen des vorherigen Modells (mit größerer Stichprobengröße) verdeutlicht den Einfluss der Stichprobengröße auf die statistische Signifikanz der Effekte.
lmer(y_h1 ~ ad_type + (ad_type | id), data = df_mixed_n20) |>
report::report_table()Parameter | Coefficient | 95% CI | t(74) | p | Effects | Group | Std. Coef. | Std. Coef. 95% CI | Fit
-----------------------------------------------------------------------------------------------------------------------------------
(Intercept) | 3.54 | [ 3.15, 3.93] | 18.20 | < .001 | fixed | | -0.03 | [-0.45, 0.40] |
ad type [not funny] | 0.05 | [-0.33, 0.43] | 0.26 | 0.799 | fixed | | 0.05 | [-0.36, 0.47] |
| 0.70 | | | | random | id | | |
| 0.46 | | | | random | id | | |
| -0.84 | | | | random | id | | |
| 0.73 | | | | random | Residual | | |
| | | | | | | | |
AIC | | | | | | | | | 216.78
AICc | | | | | | | | | 217.93
BIC | | | | | | | | | 231.08
R2 (conditional) | | | | | | | | | 0.38
R2 (marginal) | | | | | | | | | 7.11e-04
Sigma | | | | | | | | | 0.73Der Effekt, obwohl in der Population vorhanden, wird nun nicht mehr statistisch signifikant, wir haben also einen Beta-Fehler gemacht.
5.2 Agentenbasierte Modelle
Alternativ zur statistischen Simulation von Daten können wir auch eine eher subjektbezogene Perspektive einnehmen, d.h. wir spezifizieren sog. Agenten, die sich nach bestimmten Regeln verhalten. Dabei werden zunächst einfache Agenten definiert und später generative Agenten mithilfe von Large Language Models (LLMs) eingesetzt.
5.2.1 Einfache Agenten
Im folgenden Code wird eine einfache Funktion judge_ad() definiert, die simuliert, wie eine Person eine Anzeige bewertet. Die Bewertungsfunktion basiert auf einem Ausgangswert (3), einer zufälligen Komponente (rnorm()) und einem zusätzlichen positiven Effekt (0.3), wenn die Werbung als witzig eingestuft wird. Die nachfolgenden Aufrufe der Funktion zeigen beispielhafte Bewertungen für verschiedene Anzeigentypen.
judge_ad <- function(ad_type) {
3 + rnorm(n = 1) + (ad_type == "funny") * .3
}
judge_ad("funny")[1] 1.333383judge_ad("not_funny")[1] 3.701356Nun erstellen wir eine Population von Agenten mit verschiedenen Eigenschaften, die mit verschiedenen Anzeigen konfrontiert werden. Mit expand_grid() wird ein Dataframe erstellt, der alle möglichen Kombinationen von Alter, Anzeigentyp und Marke enthält. Anschließend wird mit mutate() eine neue Spalte hinzugefügt. Die Funktion map_dbl() wendet unserer eigene Funktion judge_ad() auf jede Zeile der Spalte ad_type an und speichert die resultierenden Bewertungen in der Spalte y.
df_agents <- expand_grid(
age = c("old", "young"),
ad_type = c("funny", "not funny"),
brand = c("BMW", "Mercedes", "Audi", "VW")
)
df_agents |> mutate(y = map_dbl(ad_type, judge_ad))# A tibble: 16 × 4
age ad_type brand y
<chr> <chr> <chr> <dbl>
1 old funny BMW 2.83
2 old funny Mercedes 2.23
3 old funny Audi 3.08
4 old funny VW 2.27
5 old not funny BMW 2.27
# ℹ 11 more rowsJeder Agent hat nun jede Anzeige bewertet. Die Daten sehen aus wie zuvor, wir können allerdings deutlich komplexere Agenten mit eigenen Bewertungsfunktionen konstruieren.
5.2.2 Generative Agenten
Die Erstellung von Regeln ist bei agentenbasierten Simulationen oft sehr schwierig, weshalb in jüngster Zeit sog. generative Agentenmodelle verwendet werden. Dieser Abschnitt nutzt das tidyllm-Paket und ein Large Language Model, um realistischere Agentenantworten zu generieren, die auf rein textbasierten Aufgaben basieren statt auf algorithmischen Simulationen des datengenerierenden Prozesses.
Hier wird eine Aufgabe (task) definiert, die einen generativen Agenten in eine bestimmte Situation versetzt. Die Funktion llm_message() erstellt eine Nachricht für das LLM,und sendet diese Nachricht an das LLM. Der Parameter .temperature steuert die Zufälligkeit der Antwort. .json_schema definiert das erwartete Format der Antwort (ein JSON-Objekt mit numerischen Werten für “ad_liking” und “buy_intention”). Die abschließende Funktion get_reply_data() extrahiert die Antwort des Modells im gewünschten Format.
task <- "Imagine you are looking for a car and checking out ads from different brands.
You see an ad by BMW with the claim 'Honestly now,
did you spend your youth dreaming about someday owning a Nissan or a Mitsubishi?'.
How much do you like the ad - from 1 (not at all) - 5 (very much)?
And how likely are you going to buy the car - from 1 (not at all) - 5 (very likely)?"
llm_message(task) |>
chat(gemini(),
.temperature = .5,
.json_schema = tidyllm_schema(ad_liking = "numeric", buy_intention = "numeric")
) |>
get_reply_data()$ad_liking
[1] 2
$buy_intention
[1] 2Wir erhalten 2 Spalten mit den Antworten des LLM.
Im nächsten Schritt generieren wir Aufgaben für die verschiedenen Agenten aus dem obigen df_agents Datensatz. Zuerst wird basierend auf dem Anzeigentyp ein spezifischer Werbespruch (claim) zugeordnet Anschließend wird mit glue::glue() für jede Kombination von Alter, Marke und Werbespruch eine personalisierte Aufgabe (task) formuliert, die dem LLM gestellt werden soll. Dafür werden Platzhalter im Format {Spalte} zeilenweise ausgefüllt.
df_tasks <- df_agents |>
mutate(claim = ifelse(ad_type == "funny",
"Honestly now, did you spend your youth dreaming about someday owning a Nissan or a Mitsubishi?",
"Refined elegance. Raw power."
)) |>
mutate(task = glue::glue("Imagine you are an interested {age} person looking for a car and checking out ads from different brands.
You see an ad by {brand} with the claim '{claim} - {brand}'.
How much do you like the ad - from 1 (not at all) - 5 (very much)?
And how likely are you going to buy the car - from 1 (unlikely) - 5 (very likely)?"))
df_tasks |>
select(task)# A tibble: 16 × 1
task
<glue>
1 Imagine you are an interested old person looking for a car and checking out a…
2 Imagine you are an interested old person looking for a car and checking out a…
3 Imagine you are an interested old person looking for a car and checking out a…
4 Imagine you are an interested old person looking for a car and checking out a…
5 Imagine you are an interested old person looking for a car and checking out a…
# ℹ 11 more rowsZum Schluss werden die generierten Aufgaben an das LLM gesendet und die Antworten verarbeitet. Der Befehl map() iteriert über jede Aufgabe in der Spalte task und sendet sie an das Gemini-Modell. Die Antworten werden als Listen in der Spalte answers gespeichert. Anschließend wird mit unnest_wider() die Liste in separate Spalten (ad_liking und buy_intention) aufgespalten, und die ursprüngliche Aufgabenspalte wird entfernt.
df_results <- df_tasks |>
mutate(answers = map(task, ~ llm_message(.x) |>
chat(openai(),
.json_schema = tidyllm_schema(
ad_liking = "numeric",
buy_intention = "numeric"
),
.temperature = .5
) |>
get_reply_data()))
df_results <- df_results |>
unnest_wider(answers) |>
select(-task)
df_results# A tibble: 16 × 6
age ad_type brand claim ad_liking buy_intention
<chr> <chr> <chr> <chr> <int> <int>
1 old funny BMW Honestly now, did you spend … 3 2
2 old funny Mercedes Honestly now, did you spend … 4 3
3 old funny Audi Honestly now, did you spend … 3 3
4 old funny VW Honestly now, did you spend … 4 3
5 old not funny BMW Refined elegance. Raw power. 3 2
# ℹ 11 more rowsDer resultierende Dataframe df_results enthält die simulierten Input-Informationen und die generierten Antworten des LLMs.
Abschließend wird wieder ein t-Test durchgeführt, um zu untersuchen, ob es einen signifikanten Unterschied in der Kaufabsicht zwischen den beiden Anzeigentypen gibt, basierend auf den generierten Antworten der LLM-Agenten.
df_results |>
group_by(ad_type) |>
summarise(m_buy = mean(buy_intention))# A tibble: 2 × 2
ad_type m_buy
<chr> <dbl>
1 funny 2.62
2 not funny 2.88t.test(buy_intention ~ ad_type, df_results) |>
report::report_table()Welch Two Sample t-test
Parameter | Group | Mean_Group1 | Mean_Group2 | Difference | 95% CI | t(12.36) | p | d | d CI
---------------------------------------------------------------------------------------------------------------------------
buy_intention | ad_type | 2.62 | 2.88 | -0.25 | [-0.73, 0.23] | -1.13 | 0.281 | -0.64 | [-1.77, 0.51]
Alternative hypothesis: two.sidedInteressanterweise führen in den LLM-basierten Simulationen die witzigen Anzeigen im Schnitt zu geringerer Kaufabsicht, wenn auch nicht statistisch signifikant. Dies ist aber kein empirisches Ergebnis, sondern reproduziert lediglich das Weltwissen und die Biases, die in den Trainingsdaten des Modells vorhanden sind.