library(lavaan)
library(tidyverse)
library(report)
theme_set(theme_minimal())4 Lagged und Cross-Lagged Modelle
Stevic, A., Schmuck, D., Thomas, M. F., Karsay, K., & Matthes, J. (2023). Distracted Children? Nighttime Smartphone Use, Children’s Attentional Problems, and School Performance Over Time. The Journal of Early Adolescence, 44(2), 223–249. https://doi.org/10.1177/02724316231164734
4.1 Pakete und Daten
Wir laden zunächst die notwendigen R-Pakete. Für Pfadanalysen benötigen wir wieder das lavaan-Paket. Wie immer laden wir tidyverse und report.
Als Datensatz verwenden wir eine Zwei-Wellen-Panel-Befragung von Stevic et al. Hier wurden Kinder und Eltern zur (abendlichen) Mediennutzung, Aufmerksamkeitsdefiziten und der Leistung in der Schule befragt.
d_stevic <- haven::read_sav("data/stevic_etal.sav") |>
mutate(female_child = if_else(gender_child_w1 == 1, 1, 0)) |>
haven::zap_labels()
d_stevic# A tibble: 822 × 79
consent_w1 gender_parent_w1 age_parent_w1 education_parent_w1
<dbl> <dbl> <dbl> <dbl>
1 1 2 44 7
2 1 1 44 7
3 1 2 42 3
4 1 1 38 7
5 1 1 40 4
# ℹ 817 more rows
# ℹ 75 more variables: kids_home_parent_w1 <dbl>, nr_children__parent_w1 <dbl>,
# age_participating_child_w1 <dbl>, smartphone_parents_w1 <dbl>,
# smartphone_child_w1 <dbl>, attention1_parent_w1 <dbl>,
# attention2_parent_w1 <dbl>, attention3_parent_w1 <dbl>,
# income_parent_w1 <dbl>, gender_child_w1 <dbl>, age_child_w1 <dbl>,
# education_child_w1 <dbl>, performance1_child_w1 <dbl>, …d_stevic |>
select(female_child, w1_nightuse_child_w1, w2_nightuse_child_w2, attention_parent_w1, attention_parent_w2) |>
report::report_table()Variable | n_Obs | Mean | SD | Median | MAD | Min | Max | Skewness | Kurtosis | percentage_Missing
-------------------------------------------------------------------------------------------------------------------
female_child | 822 | 0.51 | 0.50 | 1.00 | 0.00 | 0.00 | 1.00 | -0.04 | -2.00 | 0.00
w1_nightuse_child_w1 | 822 | 1.87 | 1.27 | 1.25 | 0.37 | 1.00 | 7.00 | 1.85 | 2.77 | 0.00
w2_nightuse_child_w2 | 822 | 1.77 | 1.19 | | 0.37 | 1.00 | 7.00 | 2.15 | 4.64 | 53.28
attention_parent_w1 | 822 | 2.73 | 1.12 | 2.67 | 0.99 | 1.00 | 5.00 | 0.21 | -0.83 | 0.00
attention_parent_w2 | 822 | 2.67 | 1.11 | | 0.99 | 1.00 | 5.00 | 0.17 | -0.82 | 53.28Ein Blick auf die Deskriptivstatistiken verrät, dass weniger als die Hälfte der Befragten zum 2. Messzeitpunkt noch geantwortet haben, wir also eine recht starke Panelmortalität haben.
4.2 Autokorrelation, -regression und Lagged Dependent Variable (LDV)
4.2.1 Autokorrelationen
Zunächst betrachten wir die Stabilität der beiden zentralen Variablen: nächtliche Social-Media-Nutzung (Selbstbericht der Kinder) und Aufmerksamkeitsschwierigkeiten (beurteilt durch die Eltern).
cor.test(~ w1_nightuse_child_w1 + w2_nightuse_child_w2, d_stevic) |>
report_table()Pearson's product-moment correlation
Parameter1 | Parameter2 | r | 95% CI | t(382) | p
-----------------------------------------------------------------------------------
w1_nightuse_child_w1 | w2_nightuse_child_w2 | 0.51 | [0.43, 0.58] | 11.67 | < .001
Alternative hypothesis: two.sidedEs besteht eine mittlere Korrelation zwischen den Messungen der nächtlichen Mediennutzung, d.h. die Test-Retest-Reliabilität und/oder Stabilität des Mediennutzungsverhaltens ist moderat.
cor.test(~ attention_parent_w1 + attention_parent_w2, d_stevic) |>
report::report_table()Pearson's product-moment correlation
Parameter1 | Parameter2 | r | 95% CI | t(382) | p
---------------------------------------------------------------------------------
attention_parent_w1 | attention_parent_w2 | 0.72 | [0.67, 0.76] | 20.21 | < .001
Alternative hypothesis: two.sidedDie Autokorrelation bei den (von den Eltern angegebenen) Aufmerksamkeitsdefiziten ist etwas stärker ausgeprägt, d.h. die Einschätzung ist reliabler und/oder stabiler über die Zeit. Einfach formuliert: Kinder, die schon zum ersten Messzeitpunkt relativ starke/geringe Aufmerksamkeitsdefizite aufwiesen (laut Eltern), taten dies auch zum zweiten Messzeitpunkt. Die Rangreihe der Kinder ist also relativ stabil über die Zeit.
4.2.2 Regression ohne und mit LDV
Das naive Regressionsmodell versucht, die Aufmerksamkeitsdefizite zu \(t_2\) durch die nächtliche Social-Media-Nutzung zu \(t_1\) vorherzusagen.
results_naiv <- lm(attention_parent_w2 ~ w1_nightuse_child_w1, d_stevic)
report::report_table(results_naiv)Parameter | Coefficient | 95% CI | t(382) | p | Std. Coef. | Std. Coef. 95% CI | Fit
--------------------------------------------------------------------------------------------------------------
(Intercept) | 2.44 | [2.24, 2.64] | 24.28 | < .001 | -2.77e-16 | [-0.10, 0.10] |
w1 nightuse child w1 | 0.13 | [0.03, 0.22] | 2.71 | 0.007 | 0.14 | [ 0.04, 0.24] |
| | | | | | |
AIC | | | | | | | 1167.42
AICc | | | | | | | 1167.48
BIC | | | | | | | 1179.27
R2 | | | | | | | 0.02
R2 (adj.) | | | | | | | 0.02
Sigma | | | | | | | 1.10Es scheint einen positiven, statistisch signifikanten Einfluss der nächtlichen Mediennutzung auf spätere Aufmerksamkeitsdefizite zu geben. Was passiert, wenn wir die zuvor erhobenen Aufmerksamkeitsprobleme zu \(t_1\) im Modell berücksichtigen? Dies entspricht dem klassischen LDV-Modell.
results_ldv <- lm(attention_parent_w2 ~ w1_nightuse_child_w1 + attention_parent_w1, d_stevic)
report::report_table(results_ldv)Parameter | Coefficient | 95% CI | t(381) | p | Std. Coef. | Std. Coef. 95% CI | Fit
--------------------------------------------------------------------------------------------------------------
(Intercept) | 0.58 | [ 0.35, 0.81] | 5.00 | < .001 | -3.56e-16 | [-0.07, 0.07] |
w1 nightuse child w1 | 0.05 | [-0.01, 0.12] | 1.62 | 0.106 | 0.06 | [-0.01, 0.13] |
attention parent w1 | 0.72 | [ 0.65, 0.79] | 19.95 | < .001 | 0.71 | [ 0.64, 0.78] |
| | | | | | |
AIC | | | | | | | 894.84
AICc | | | | | | | 894.95
BIC | | | | | | | 910.64
R2 | | | | | | | 0.52
R2 (adj.) | | | | | | | 0.52
Sigma | | | | | | | 0.77Berücksichtigen wir die bereits zum ersten Messzeitpunkt gemessenen Aufmerksamkeitsproblem, wird der geschätzte Effekt der nächtlichen Mediennutzung deutlich kleiner und statistisch nicht-signifikant (auch wenn wir bei einer gerichteten Hypothese wie oben einseitig testen würden). Anders formuliert: Wenn wir in Rechnung stellen, dass manche Kinder bereits bei der ersten Messung viele/wenige Aufmerksamkeitsdefizite hatten, finden wir nur einen kleinen, nicht signfikanten Medieneffekt. Dies ist sehr häufig der Fall.
Der Koeffizient der Lagged Dependent Variable sollte nicht als Verstärkungs/Abschwächungseffekt interpretiert werden, d.h. ein positiver Koeffizient bedeutet nicht unbedingt, dass Kinder mit Aufmerksamkeitsproblemen zu \(t_1\) noch mehr Aufmerksamkeitsprobleme zu \(t_2\) hatten, sondern wie oben beschrieben, die Rangfolge der Kinder nach Aufmerksamkeitsproblem bleibt relativ stabil. Folgende 3 Muster haben alle einen standardisierten Autoregressionseffekt von 1:
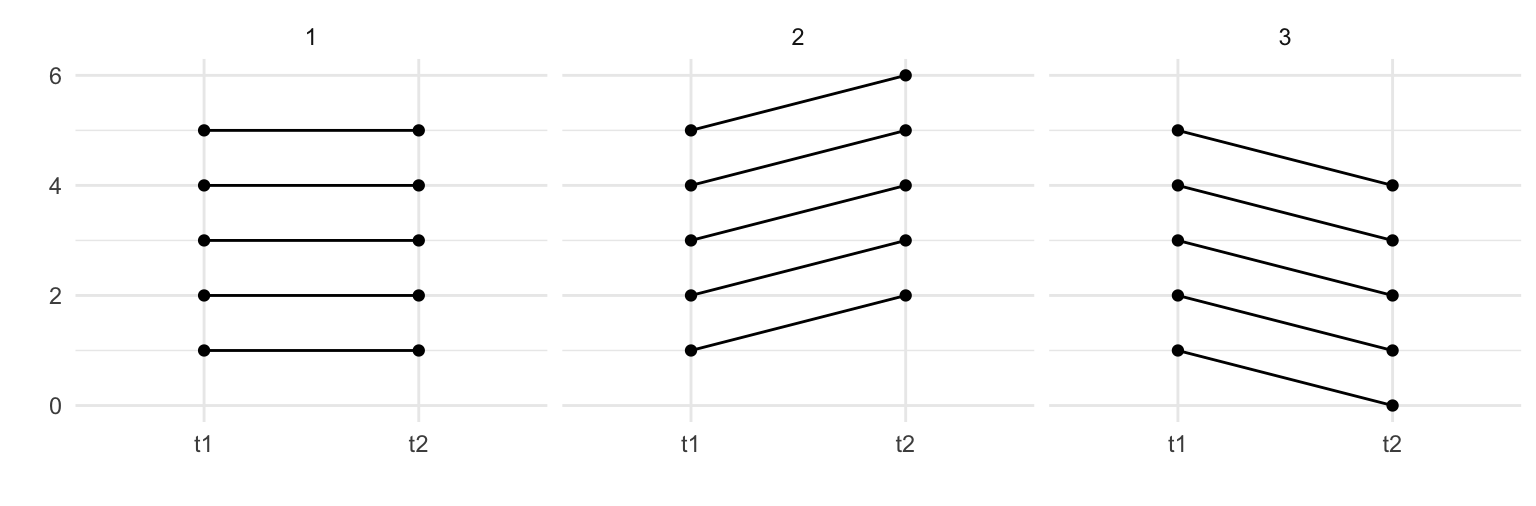
Umgekehrt können wir auch untersuchen, ob Kinder mit Aufmerksamkeitsdefiziten eher zu nächtlicher Social-Media-Nutzung neigen. Diesmal schätzen wir gleich das LDV-Modell, d.h. wir berücksichtigen die zu \(t_1\) berichtete Mediennutzung.
results_ldv2 <- lm(w2_nightuse_child_w2 ~ w1_nightuse_child_w1 + attention_parent_w1, d_stevic)
report::report_table(results_ldv2)Parameter | Coefficient | 95% CI | t(381) | p | Std. Coef. | Std. Coef. 95% CI | Fit
---------------------------------------------------------------------------------------------------------------
(Intercept) | 0.64 | [ 0.34, 0.94] | 4.15 | < .001 | -1.08e-15 | [-0.09, 0.09] |
w1 nightuse child w1 | 0.50 | [ 0.41, 0.59] | 11.43 | < .001 | 0.50 | [ 0.42, 0.59] |
attention parent w1 | 0.09 | [-0.01, 0.18] | 1.83 | 0.068 | 0.08 | [-0.01, 0.17] |
| | | | | | |
AIC | | | | | | | 1108.52
AICc | | | | | | | 1108.62
BIC | | | | | | | 1124.32
R2 | | | | | | | 0.27
R2 (adj.) | | | | | | | 0.27
Sigma | | | | | | | 1.02Der Zusammenhang ist nicht-signifikant bei einem zweiseitigen Test, allerdings dürften wir bei einer gerichteten Hypothese wie oben den p-Wert halbieren.
4.3 Cross-lagged Panel Model (CLPM)
4.3.1 Bivariates CLPM
Wie bei den Mediationsanalysen können wir statt zwei separater Regressionen auch ein einzelnes Pfadmodell rechnen, um beide reziproken Pfade gleichzeitig zu schätzen. Hierfür verwenden wir wieder das lavaan-Paket und den dort üblichen Ablauf aus Modellspezifikation und anschließender Schätzung. Das Cross-Lagged-Panel-Modell wird mit derselben Modellformel wie die Einzelregressionen spezifiziert:
clp_model <- "
attention_parent_w2 ~ w1_nightuse_child_w1 + attention_parent_w1
w2_nightuse_child_w2 ~ w1_nightuse_child_w1 + attention_parent_w1
w1_nightuse_child_w1 ~~ attention_parent_w1
"
results_clpm <- lavaan::sem(clp_model, data = d_stevic)
summary(results_clpm, standardized = TRUE, rsquare = TRUE)lavaan 0.6-18 ended normally after 15 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 10
Used Total
Number of observations 384 822
Model Test User Model:
Test statistic 0.000
Degrees of freedom 0
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Regressions:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
attention_parent_w2 ~
w1_nghts_chl_1 0.054 0.033 1.625 0.104 0.054 0.058
attntn_prnt_w1 0.723 0.036 20.025 0.000 0.723 0.712
w2_nightuse_child_w2 ~
w1_nghts_chl_1 0.500 0.044 11.470 0.000 0.500 0.504
attntn_prnt_w1 0.087 0.048 1.836 0.066 0.087 0.081
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
w1_nightuse_child_w1 ~~
attntn_prnt_w1 0.145 0.067 2.167 0.030 0.145 0.111
.attention_parent_w2 ~~
.w2_nghts_chl_2 0.075 0.040 1.891 0.059 0.075 0.097
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.attntn_prnt_w2 0.590 0.043 13.856 0.000 0.590 0.480
.w2_nghts_chl_2 1.028 0.074 13.856 0.000 1.028 0.731
w1_nghts_chl_1 1.425 0.103 13.856 0.000 1.425 1.000
attntn_prnt_w1 1.194 0.086 13.856 0.000 1.194 1.000
R-Square:
Estimate
attntn_prnt_w2 0.520
w2_nghts_chl_2 0.269Im Output-Block Regressions erhalten wir dieselben Koeffizienten wie zuvor. Zusätzlich können wir im Block Covariances noch die Korrelation zwischen den beiden Variablen zu \(t_1\) sehen (r = .111) sowie die Korrelation der Residuen der beiden Variablen zu \(t_2\). Letzteres ist der Zusammenhang nach Kontrolle der autoregressiven und der cross-lagged Effekte. Ist dieser signifikant, deutet dies zumeist auf eine nicht-berücksichtigte Drittvariable hin.
4.3.2 CLPM mit Kovariaten
Das CLPM kann mit beliebigen zeitlich variierenden oder nicht variierenden Variablen erweitert werden. Als Beispiel kontrollieren wir statistisch für das Ge der Kinder. Hierfür erweitern wir die Spefizikation, so dass für beide Variablen der Prädiktor female_child hinzukommt.
clp_model_age <- "
attention_parent_w2 ~ w1_nightuse_child_w1 + attention_parent_w1 + female_child
w2_nightuse_child_w2 ~ w1_nightuse_child_w1 + attention_parent_w1 + female_child
w1_nightuse_child_w1 ~ female_child
attention_parent_w1 ~ female_child
w1_nightuse_child_w1 ~~ attention_parent_w1
"
results_clpm_age <- lavaan::sem(clp_model_age, data = d_stevic)
summary(results_clpm_age, standardized = TRUE, rsquare = TRUE)lavaan 0.6-18 ended normally after 11 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 14
Used Total
Number of observations 384 822
Model Test User Model:
Test statistic 0.000
Degrees of freedom 0
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Regressions:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
attention_parent_w2 ~
w1_nghts_chl_1 0.053 0.033 1.582 0.114 0.053 0.057
attntn_prnt_w1 0.723 0.036 19.990 0.000 0.723 0.713
female_child 0.020 0.079 0.247 0.805 0.020 0.009
w2_nightuse_child_w2 ~
w1_nghts_chl_1 0.488 0.044 11.177 0.000 0.488 0.491
attntn_prnt_w1 0.096 0.047 2.014 0.044 0.096 0.088
female_child 0.240 0.104 2.305 0.021 0.240 0.101
w1_nightuse_child_w1 ~
female_child 0.276 0.121 2.279 0.023 0.276 0.116
attention_parent_w1 ~
female_child -0.131 0.112 -1.178 0.239 -0.131 -0.060
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.w1_nightuse_child_w1 ~~
.attntn_prnt_w1 0.154 0.066 2.320 0.020 0.154 0.119
.attention_parent_w2 ~~
.w2_nghts_chl_2 0.074 0.040 1.875 0.061 0.074 0.096
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.attntn_prnt_w2 0.589 0.043 13.856 0.000 0.589 0.480
.w2_nghts_chl_2 1.014 0.073 13.856 0.000 1.014 0.721
.w1_nghts_chl_1 1.406 0.101 13.856 0.000 1.406 0.987
.attntn_prnt_w1 1.190 0.086 13.856 0.000 1.190 0.996
R-Square:
Estimate
attntn_prnt_w2 0.520
w2_nghts_chl_2 0.279
w1_nghts_chl_1 0.013
attntn_prnt_w1 0.004Wir erkennen, dass Mädchen signifikant häufiger nachts Social Media genutzt haben, während es bei den Aufmerksamkeitsproblemen keine signifikanten Unterschiede zwischen Jungen und Mädchen gab.
4.4 Glossar
| Funktion | Definition |
|---|---|
| cor.test | Korrelation und Signifikanz schätzen |
4.5 Hausaufgabe
Untersuchen Sie den längsschnittlichen Zusammenhang zwischen nächtlicher Social-Media-Nutzung und schulischen Leistungen (obj_performance_child_wX).