library(lme4)
library(marginaleffects)
library(tidyverse)
library(report)
theme_set(theme_minimal())5 Multilevel-Längsschnittanalyse
TipQuelle
Johannes, N., Dienlin, T., Bakhshi, H., & Przybylski, A. K. (2022). No effect of different types of media on well-being. Scientific Reports, 12(1). https://doi.org/10.1038/s41598-021-03218-7
5.1 Pakete und Daten
Wir laden zunächst die notwendigen R-Pakete. Für die Multilevel-Modelle verwenden wir das lme4-Paket, für die Modellvorhersagen marginaleffects. Wie immer laden wir tidyverse und report und setzen ein schöneres Theme.
Als Datensatz verwenden wir eine Studie von Johannes et al., bei der dieselben Befragten 6 Wochen lang unterschiedliche Mediennutzung und Lebenszufriedenheit berichtet haben. Der Datensatz ist im sog. Langformat, d.h. die Daten aller Wellen werden aufeinander gestapelt, dementsprechend gibt es n = Personen x Wellen Datenzeilen. Die Personen sind mit der Variable id gekennzeichnet, die Erhebungswoche mit wave. Die weiteren Variablen geben dann jeweils die Messung einer Person in einer Woche wieder, stabile Personenmerkmale wie Alter wiederholen sich entsprechend pro Person.
d_johannes <- read_rds("data/johannes_etal.rds") |>
filter(wave >= 2) |>
filter(!is.na(tv_time))
d_johannes# A tibble: 8,882 × 122
id gender wave age filter_music filter_films filter_tv
<fct> <fct> <dbl> <dbl> <dbl> <dbl> <dbl>
1 pp_2 Female 2 22 1 0 0
2 pp_2 Female 3 22 1 0 0
3 pp_2 Female 5 22 1 0 0
4 pp_3 Male 2 43 1 1 0
5 pp_3 Male 3 43 1 1 0
# ℹ 8,877 more rows
# ℹ 115 more variables: filter_video_games <dbl>, filter_ebooks <dbl>,
# filter_magazines <dbl>, filter_audiobooks <dbl>, music_estimate <dbl>,
# music_identity_1 <dbl>, music_identity_2 <dbl>, music_identity_3 <dbl>,
# music_identity_4 <dbl>, music_identity_5 <dbl>, music_identity_6 <dbl>,
# music_identity_7 <dbl>, music_time <dbl>, music_identity <dbl>,
# films_estimate <dbl>, films_identity_1 <dbl>, films_identity_2 <dbl>, …Da der Datensatz im sog. Langformat ist, gibt es mehrere Zeilen pro Person (eine pro Welle). Wir zählen mit n_distinct() die tatsächliche Personenstichprobe:
n_distinct(d_johannes$id)[1] 2159Zudem schauen wir uns die Deskriptivstatistiken der relevanten Variablen an.
d_johannes |>
select(wave, life_satisfaction, tv_time, gender) |>
report::report_table()Variable | Level | n_Obs | percentage_Obs | Mean | SD | Median
--------------------------------------------------------------------------
wave | | 8882 | | 3.71 | 1.32 | 4
life_satisfaction | | 8882 | | 6.40 | 2.09 | 7
tv_time | | 8882 | | 3.37 | 3.30 | 3
gender | Other | 5 | 0.06 | | |
gender | Male | 4283 | 48.22 | | |
gender | Female | 4594 | 51.72 | | |
Variable | MAD | Min | Max | Skewness | Kurtosis | percentage_Missing
-------------------------------------------------------------------------------
wave | 1.48 | 2 | 6 | 0.21 | -1.12 | 0
life_satisfaction | 1.48 | 0 | 10 | -0.85 | 0.48 | 0
tv_time | 2.97 | 0 | 22 | 1.90 | 5.30 | 0
gender | | | | | |
gender | | | | | |
gender | | | | | | Wir können an der Deskriptivstatistik erkennen, dass Daten über 5 Wochen (Wave 2-6, Woche 1 ist laut Autoren problematisch und wird daher ausgeschlossen) vorliegen und die Befragten im Mittel etwas über 3,5h TV am Tag sehen (SD 3,3h).
5.2 Naives OLS-Modell (pooling)
Im folgenden Beispiel wollen wir den Zusammenhang zwischen der TV-Nutzung und allgemeiner Lebenszufriedenheit untersuchen. Das naive Regressionsmodell ignoriert die Schachtelung bzw. Nicht-Unabhängigkeit der Daten und tut so, als hätten wir n = 8882 unabhängige Fälle.
results_ols <- lm(life_satisfaction ~ tv_time, data = d_johannes)
report::report_table(results_ols)Parameter | Coefficient | 95% CI | t(8880) | p | Std. Coef.
--------------------------------------------------------------------------
(Intercept) | 6.47 | [ 6.41, 6.53] | 204.44 | < .001 | -1.66e-15
tv time | -0.02 | [-0.03, -0.01] | -3.00 | 0.003 | -0.03
| | | | |
AIC | | | | |
AICc | | | | |
BIC | | | | |
R2 | | | | |
R2 (adj.) | | | | |
Sigma | | | | |
Parameter | Std. Coef. 95% CI | Fit
------------------------------------------
(Intercept) | [-0.02, 0.02] |
tv time | [-0.05, -0.01] |
| |
AIC | | 38281.92
AICc | | 38281.92
BIC | | 38303.19
R2 | | 1.02e-03
R2 (adj.) | | 9.03e-04
Sigma | | 2.09Der Effekt der TV-Nutzung ist negativ und statistisch signifikant, aber wir wissen, dass dieser Schätzer und der Standardfehler verzerrt sind. Im Folgenden verwenden wir Multilevel-Modelle, die die Schachtelung bzw. Nicht-Unabhängigkeit der Paneldaten explizit abbilden.
5.3 Random Effects Modell
Im Random Effects Modell werden die Messungen auf Level 1 und die Befragten auf Level 2 betrachtet, die Schachtelung der Daten wird also explizit im Modell abgebildet. Die Annahme dabei ist, dass die Unterschiede in der mittleren Lebenszufriedenheit der Befragten einer Normalverteilung folgen, d.h. manche Befragten sind im Mittel (un-)zufriedener als andere. Dieses Modell wird als Random Intercept Modell bezeichnet, wobei random hier nicht bedeutet, dass die Intercepts pro Person rein zufällig streuen, sondern sie einer Zufallsvariable (Normalverteilung) entsprechen, daher bezeichnen wir es auch lieber als Varying Intercept Modell
In R kann man Multilevel-Modelle mit dem lme4-Paket schätzen. Die Random (oder besser: nach Personen variierenden) Intercepts werden mit (1 | id) spezifiziert.
results_re <- lme4::lmer(life_satisfaction ~ tv_time + (1 | id), data = d_johannes)
report::report_table(results_re)Parameter | Coefficient | 95% CI | t(8878) | p | Effects
---------------------------------------------------------------------------
(Intercept) | 6.42 | [ 6.33, 6.51] | 140.43 | < .001 | fixed
tv time | -5.74e-03 | [-0.02, 0.00] | -1.18 | 0.239 | fixed
| 1.94 | | | | random
| 0.75 | | | | random
| | | | |
AIC | | | | |
AICc | | | | |
BIC | | | | |
R2 (conditional) | | | | |
R2 (marginal) | | | | |
Sigma | | | | |
Parameter | Group | Std. Coef. | Std. Coef. 95% CI | Fit
-----------------------------------------------------------------------
(Intercept) | | -8.95e-04 | [-0.04, 0.04] |
tv time | | -9.06e-03 | [-0.02, 0.01] |
| id | | |
| Residual | | |
| | | |
AIC | | | | 27350.19
AICc | | | | 27350.19
BIC | | | | 27378.55
R2 (conditional) | | | | 0.87
R2 (marginal) | | | | 8.25e-05
Sigma | | | | 0.75Die Ergebnisse des RE-Modells zeigen einen winzigen, nicht-signifikanten Effekt der TV-Nutzung auf die Lebenszufriedenheit, was den Ergebnissen des naiven OLS-Modells oben widerspricht.
Eine Stärke des Multilevel-Modells ist, dass problemlos sowohl variierende als auch stabile (Personen-)Variablen als Prädiktoren in das Modell aufgenommen werden können, z.B. Geschlecht:
results_re_gender <- lme4::lmer(life_satisfaction ~ tv_time + gender + (1 | id), data = d_johannes)
report::report_table(results_re_gender)Parameter | Coefficient | 95% CI | t(8876) | p | Effects
---------------------------------------------------------------------------
(Intercept) | 6.46 | [ 6.33, 6.58] | 101.45 | < .001 | fixed
tv time | -5.71e-03 | [-0.02, 0.00] | -1.17 | 0.241 | fixed
gender [Female] | -0.07 | [-0.24, 0.10] | -0.84 | 0.402 | fixed
gender [Other] | -0.75 | [-4.62, 3.12] | -0.38 | 0.705 | fixed
| 1.94 | | | | random
| 0.75 | | | | random
| | | | |
AIC | | | | |
AICc | | | | |
BIC | | | | |
R2 (conditional) | | | | |
R2 (marginal) | | | | |
Sigma | | | | |
Parameter | Group | Std. Coef. | Std. Coef. 95% CI | Fit
-----------------------------------------------------------------------
(Intercept) | | 0.02 | [-0.04, 0.07] |
tv time | | -9.02e-03 | [-0.02, 0.01] |
gender [Female] | | -0.03 | [-0.11, 0.05] |
gender [Other] | | -0.36 | [-2.21, 1.49] |
| id | | |
| Residual | | |
| | | |
AIC | | | | 27353.24
AICc | | | | 27353.25
BIC | | | | 27395.79
R2 (conditional) | | | | 0.87
R2 (marginal) | | | | 4.47e-04
Sigma | | | | 0.75Wir erkennen, dass es keine signifikanten Geschlechtsunterschiede in der Lebenszufriedenheit gibt, obwohl zumindest in der Stichprobe Frauen und vor allem andere Geschlechter etwas weniger zufrieden sind.
5.4 REWB Modell
Obwohl das RE-Modell deutlich flexibler in der Anwendung ist, wird es in der Praxis oft kritisiert, weil beim RE-Modell nicht gewährleistet ist, dass der Effekt des Prädiktors als kausaler Effekt unter Kontrolle aller beobachteten und unbeobachteten Unterschiede zwischen den Befragten zu interpretieren ist. Dies kann man aber durch eine spezielle Spezifikation des Modells als Random Effects Within-Between (REWB) Modell beheben, das einen unverzerrten Schätzer des kausalen Within-Person-Effekts liefert und gleichzeitig beliebige weitere Kovariaten flexibel integriert.
Praktisch wird jede Prädiktorvariable in einen Within-Person und einen Between-Person-Bestandteil zerlegt. Konkret ist der Within-Bestandteil die Abweichung der wöchentlichen TV-Nutzung vom eigenen Personenmittelwert: Eine Person, die im Mittel 4h TV pro Tag nutzt und in Woche 3 nur 2h, erhält in dieser Woche den Wert −2. Der Koeffizient des Within-Terms gibt damit an, um wie viel sich die Lebenszufriedenheit derselben Person ändert, wenn sie in einer Woche eine Stunde mehr TV gesehen hat als im eigenen Schnitt — stabile Unterschiede zwischen Personen (beobachtete wie unbeobachtete) werden dadurch herausgerechnet. Die Between-Variable ist nichts anderes als der Personenmittelwert der TV-Nutzung einer Person über alle Wellen, also die mittlere TV-Nutzung pro Person. Die Vergleichsgruppe des Within-Effekts ist also nicht die anderen Personen, sondern die jeweils anderen Messungen derselben Person. Dazu braucht das Modell min. 3 Messungen pro Person, um überhaupt Personen-Mittelwert und Abweichungen vom Mittelwert berechnen zu können. Wir nutzen group_by() + mutate(), um den Within-Prädiktor (die Abweichung vom Personenmittelwert) und den Between-Prädiktor (den Personenmittelwert) zu erzeugen:
d_johannes <- d_johannes |>
group_by(id) |>
mutate(
tv_time_within = tv_time - mean(tv_time, na.rm = TRUE),
tv_time_between = mean(tv_time, na.rm = TRUE)
)Anschließend schätzen wir das REWB-Modell, bei dem für TV-Nutzung nun zwei Prädiktorvariablen im Modell sind - einmal within einmal between.
results_rewb <- lme4::lmer(life_satisfaction ~ tv_time_within + tv_time_between + (1 | id), data = d_johannes)
report::report_table(results_rewb)Parameter | Coefficient | 95% CI | t(8877) | p | Effects
----------------------------------------------------------------------------
(Intercept) | 6.50 | [ 6.38, 6.63] | 100.40 | < .001 | fixed
tv time within | -2.56e-03 | [-0.01, 0.01] | -0.49 | 0.622 | fixed
tv time between | -0.03 | [-0.06, 0.00] | -2.11 | 0.035 | fixed
| 1.94 | | | | random
| 0.75 | | | | random
| | | | |
AIC | | | | |
AICc | | | | |
BIC | | | | |
R2 (conditional) | | | | |
R2 (marginal) | | | | |
Sigma | | | | |
Parameter | Group | Std. Coef. | Std. Coef. 95% CI | Fit
-----------------------------------------------------------------------
(Intercept) | | -4.82e-04 | [-0.04, 0.04] |
tv time within | | -1.89e-03 | [-0.01, 0.01] |
tv time between | | -0.04 | [-0.08, 0.00] |
| id | | |
| Residual | | |
| | | |
AIC | | | | 27355.43
AICc | | | | 27355.44
BIC | | | | 27390.89
R2 (conditional) | | | | 0.87
R2 (marginal) | | | | 1.79e-03
Sigma | | | | 0.75Wie können wir nun die beiden Koeffizienten interpretieren: Der (minimale und nicht-signifikante) Within-Effekt zeigt, dass intra-individuelle Schwankungen in der wöchentlichen TV-Nutzung nicht mit Schwankungen in der Lebenszufriedenheit einhergehen. TV-Nutzung macht die Befragten offenbar weder zufriedener noch unzufriedener. Wir sehen aber am negativen Between-Effekt, dass es Unterschiede in der mittleren Lebenszufriedenheit zwischen intensiven und sporadischen TV-Nutzerinnen gibt: Personen, die im Mittel mehr fernsehen, sind im Mittel etwas unzufriedener, oder anders formuliert: Personen, die im Mittel zufriedener sind, schauen im Mittel etwas weniger fern. Diesen Between-Effekt kann man aber nicht kausal interpretieren, sondern nur als Korrelation.
Wir visualisieren hier noch einmal den Within-Effekt und sehen, dass selbst 10h mehr oder weniger tägliche TV-Nutzung als sonst die Lebenszufriedenheit nur minimal beeinflusst.
preds_rewb <- marginaleffects::avg_predictions(results_rewb, variables = "tv_time_within")
preds_rewb |>
ggplot(aes(x = tv_time_within, y = estimate, ymin = conf.low, ymax = conf.high)) +
geom_line() +
geom_ribbon(alpha = .1) +
labs(x = "difference in TV use (hours per day)", y = "Predicted life satisfaction")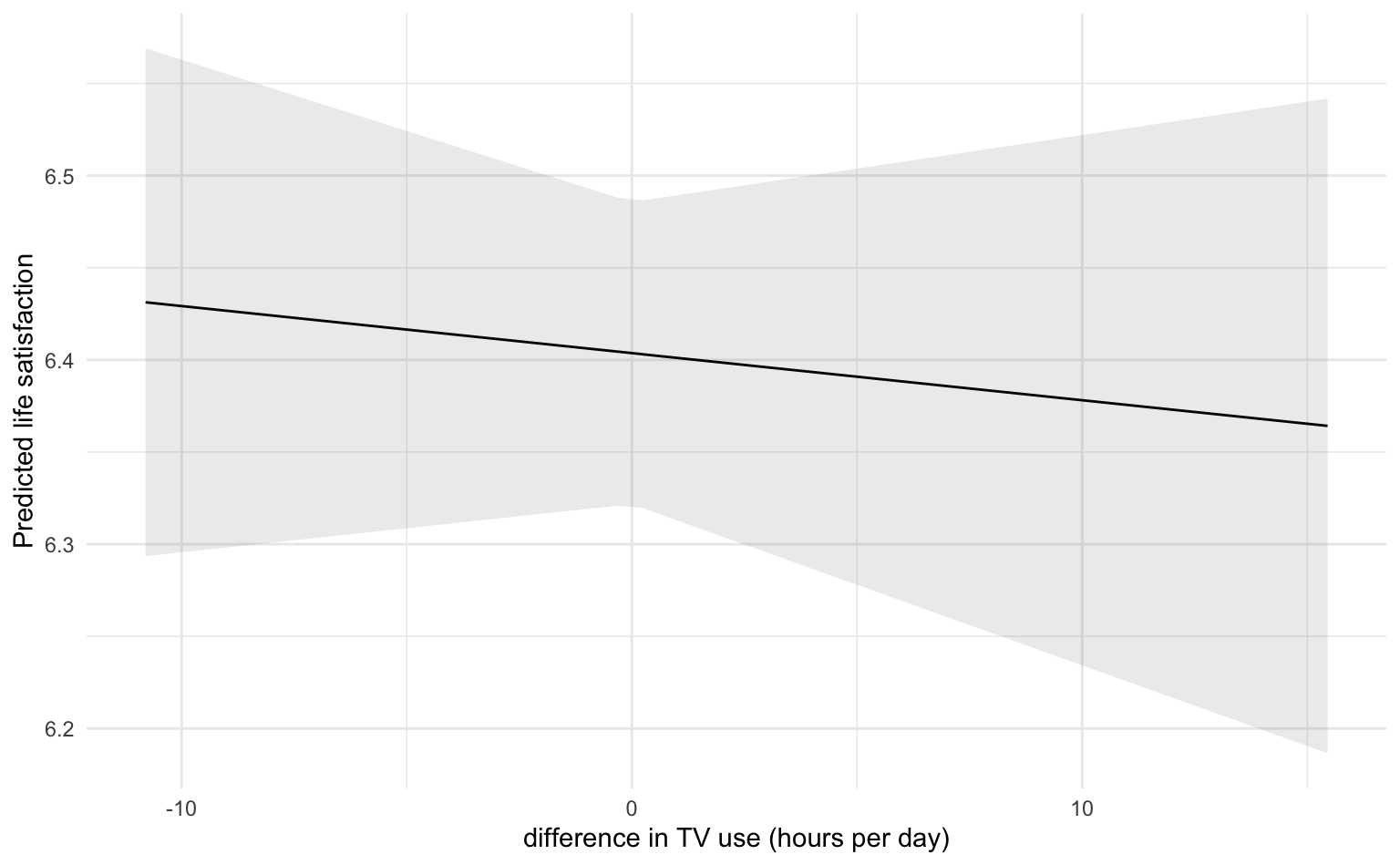
Wie zuvor können wir weitere Kovariaten ins Modell aufnehmen, sowohl auf Ebene der wöchentlichen Messung als auch auf Personenebene.
results_rewb_gender <- lme4::lmer(life_satisfaction ~ tv_time_within + tv_time_between + gender + (1 | id), data = d_johannes)
report::report_table(results_rewb_gender)Parameter | Coefficient | 95% CI | t(8875) | p | Effects
----------------------------------------------------------------------------
(Intercept) | 6.54 | [ 6.39, 6.69] | 83.91 | < .001 | fixed
tv time within | -2.56e-03 | [-0.01, 0.01] | -0.49 | 0.622 | fixed
tv time between | -0.03 | [-0.06, 0.00] | -2.09 | 0.037 | fixed
gender [Female] | -0.07 | [-0.24, 0.10] | -0.80 | 0.424 | fixed
gender [Other] | -0.78 | [-4.65, 3.08] | -0.40 | 0.692 | fixed
| 1.94 | | | | random
| 0.75 | | | | random
| | | | |
AIC | | | | |
AICc | | | | |
BIC | | | | |
R2 (conditional) | | | | |
R2 (marginal) | | | | |
Sigma | | | | |
Parameter | Group | Std. Coef. | Std. Coef. 95% CI | Fit
-----------------------------------------------------------------------
(Intercept) | | 0.02 | [-0.04, 0.07] |
tv time within | | -1.89e-03 | [-0.01, 0.01] |
tv time between | | -0.04 | [-0.08, 0.00] |
gender [Female] | | -0.03 | [-0.11, 0.05] |
gender [Other] | | -0.37 | [-2.23, 1.48] |
| id | | |
| Residual | | |
| | | |
AIC | | | | 27358.54
AICc | | | | 27358.55
BIC | | | | 27408.18
R2 (conditional) | | | | 0.87
R2 (marginal) | | | | 2.12e-03
Sigma | | | | 0.755.5 Wachstumsmodell
Neben den klassischen RE- und REWB-Modellen sind sogenannte Wachstumsmodelle in den Sozialwissenschaften weit verbreitet, vor allem im Bereich der Entwicklungspsychologie oder Jugendmedienforschung. Hier geht es zunächst gar nicht darum, den (kausalen) Effekt einer Variable auf eine andere zu schätzen, sondern zunächst zu prüfen, ob ein Outcome sich über die Zeit (linear) verändert. In unserem Beispiel könnten wir fragen, ob sich die Lebenszufriedenheit im Laufe der fünfwöchigen Studienphase verändert hat. Hierfür verwenden wir die Zeitvariable wave einfach als numerischen Prädiktor, lassen aber weiterhin personenspezifische Mittel- bzw. Ausgangswerte (Random Intercepts) zu:
results_time1 <- lme4::lmer(life_satisfaction ~ wave + (1 | id), data = d_johannes)
report::report_table(results_time1)Parameter | Coefficient | 95% CI | t(8878) | p | Effects
--------------------------------------------------------------------------
(Intercept) | 6.33 | [6.24, 6.43] | 130.67 | < .001 | fixed
wave | 0.02 | [0.01, 0.03] | 2.96 | 0.003 | fixed
| 1.94 | | | | random
| 0.75 | | | | random
| | | | |
AIC | | | | |
AICc | | | | |
BIC | | | | |
R2 (conditional) | | | | |
R2 (marginal) | | | | |
Sigma | | | | |
Parameter | Group | Std. Coef. | Std. Coef. 95% CI | Fit
-----------------------------------------------------------------------
(Intercept) | | -1.69e-04 | [-0.04, 0.04] |
wave | | 0.01 | [ 0.00, 0.02] |
| id | | |
| Residual | | |
| | | |
AIC | | | | 27342.31
AICc | | | | 27342.31
BIC | | | | 27370.68
R2 (conditional) | | | | 0.87
R2 (marginal) | | | | 1.42e-04
Sigma | | | | 0.75In der Tat sehen wir einen winzigen, positiven, statistisch signifikanten Regressionskoeffizienten für Wave: Jede Woche nahm die mittlere Lebenszufriedenheit der Befragten um 0,02 (!) Skalenpunkte zu. Der Intercept gibt den geschätzten Ausgangswert zu Woche 0 wieder, in der aber gar keine Messung stattfand. Wir können aber den Intercept durch Zentrieren der wave-Variable interpretierbarer machen.
Mithilfe von Modellvorhersagen können wir das geschätzte Wachstum auch visualisieren:
marginaleffects::avg_predictions(results_time1, variables = c("wave")) |>
ggplot(aes(
x = wave, y = estimate, ymin = conf.low, ymax = conf.high,
)) +
geom_line() +
geom_ribbon(alpha = .1) +
labs(x = "Week", y = "Predicted life satisfaction")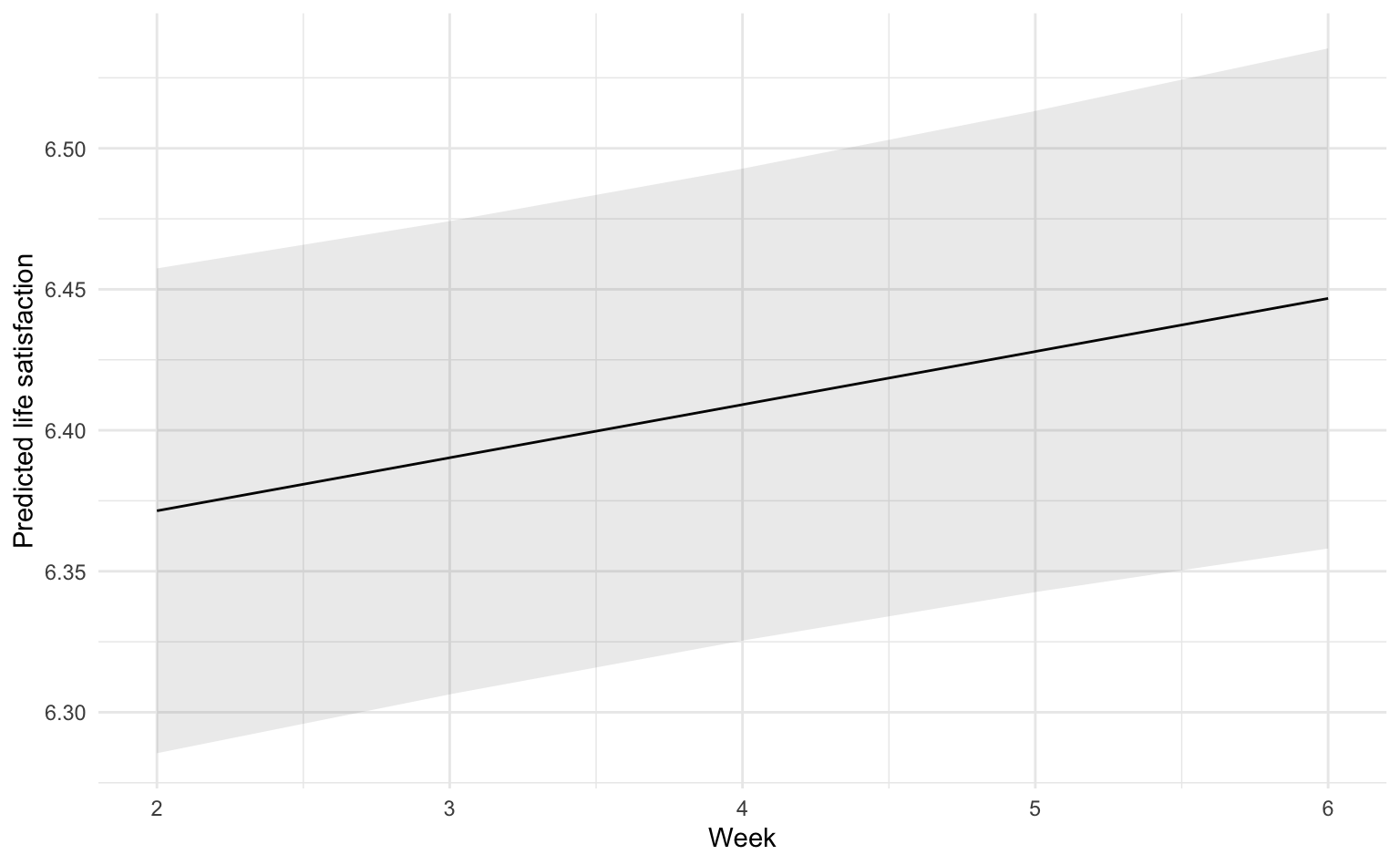
Bei Wachstumsmodellen ist die Annahme zumeist, dass nicht alle Individuen sich gleichartig entwickeln: Manche Befragten werden mit der Zeit vielleicht sehr viel zufriedener, andere unzufriedener, andere sind immer gleich zufrieden. Um dies zu modellieren, können wir den Koeffizienten für das Wachstum auch nach Personen variieren lassen (Random bzw. Varying Slope). Wir gehen also davon aus, dass Befragte unterschiedliche Ausgangswerte und unterschiedliche Entwicklungsverläufe haben können. Dies spezifizieren wir durch den Term (1 + wave | id), d.h. beides darf nach Personen variieren.
results_time2 <- lme4::lmer(life_satisfaction ~ wave + (1 + wave | id), data = d_johannes)Mit Hilfe der anova()-Funktion können wir die Güte der beiden Modelle vergleichen:
anova(results_time1, results_time2)Data: d_johannes
Models:
results_time1: life_satisfaction ~ wave + (1 | id)
results_time2: life_satisfaction ~ wave + (1 + wave | id)
npar AIC BIC logLik -2*log(L) Chisq Df Pr(>Chisq)
results_time1 4 27330 27358 -13661 27322
results_time2 6 27226 27268 -13607 27214 107.87 2 < 2.2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Wir sehen, dass das Modell mit den variierenden Intercepts und Slopes signifikant besser zu den Daten passt, d.h. es gibt bedeutsame Heterogenität in der Entwicklung der Lebenszufriedenheit. Ändert dies etwas an unserem Punktschätzer für wave?
report::report_table(results_time2)Parameter | Coefficient | 95% CI | t(8876) | p | Effects
--------------------------------------------------------------------------
(Intercept) | 6.33 | [6.24, 6.43] | 132.29 | < .001 | fixed
wave | 0.02 | [0.00, 0.03] | 2.56 | 0.011 | fixed
| 1.93 | | | | random
| 0.17 | | | | random
| -0.13 | | | | random
| 0.71 | | | | random
| | | | |
AIC | | | | |
AICc | | | | |
BIC | | | | |
R2 (conditional) | | | | |
R2 (marginal) | | | | |
Sigma | | | | |
Parameter | Group | Std. Coef. | Std. Coef. 95% CI | Fit
-----------------------------------------------------------------------
(Intercept) | | -3.24e-04 | [-0.04, 0.04] |
wave | | 0.01 | [ 0.00, 0.02] |
| id | | |
| id | | |
| id | | |
| Residual | | |
| | | |
AIC | | | | 27238.19
AICc | | | | 27238.20
BIC | | | | 27280.74
R2 (conditional) | | | | 0.88
R2 (marginal) | | | | 1.36e-04
Sigma | | | | 0.71Nein.
5.6 Glossar
| Funktion | Definition |
|---|---|
| lme4::lmer | Multilevel-Modelle schätzen |
5.7 Hausaufgabe
Untersuchen Sie den (kausalen) Zusammenhang zwischen wöchentlicher Musiknutzung (music_time) und Lebenszufriedenheit mit einem REWB-Modell und interpretieren Sie die Within- und Between-Effekte.