library(mediation)
library(lavaan)
library(tidyverse)
library(report)
theme_set(theme_minimal())3 Mediationsanalyse und Pfadmodelle
Beckert, J., Koch, T., Viererbl, B., & Schulz-Knappe, C. (2020). The disclosure paradox: how persuasion knowledge mediates disclosure effects in sponsored media content. International Journal of Advertising, 40(7), 1160–1186. https://doi.org/10.1080/02650487.2020.1859171
3.1 Pakete und Daten
Wir laden zunächst die notwendigen R-Pakete. Für Mediationsanalysen benötigen wir entweder das mediation- oder das lavaan-Paket, hier laden wir beide. Wie immer laden wir tidyverse und report.
Für die einfache Mediationsanalyse nutzen wir den SPSS_Datensatz zeitungsnutzung_mediation.sav, der nur 4 Spalten enhält: die laufende Probandennummer, politisches Wissen, politisches Interesse und Zeitungsnutzungsdauer.
d_zeitung <- haven::read_sav("data/zeitungsnutzung_mediation.sav") |>
haven::zap_labels()
d_zeitung# A tibble: 100 × 4
Subject PolWiss PolInt Zeitungsnutzungsdauer
<dbl> <dbl> <dbl> <dbl>
1 3 4 2.67 3.8
2 7 4 4.33 2.8
3 12 3.33 3.33 2.2
4 13 3.33 3 4.2
5 15 2.33 3.33 2.8
# ℹ 95 more rowsFür die multiple Mediationsanalyse verwenden wir den Experiment-Datensatz influencer_mediation.sav, der ebenfalls 4 Variablen enthält: die Versuchsbedingung Werbekennzeichnung (dichotom), sowie die beiden Variablen zum Persuasionswissen (Täuschungsabsicht und Überzeugungsabsicht) sowie die Reaktanz.
d_influencer <- haven::read_sav("data/influencer_mediation.sav") |>
haven::zap_labels()
d_influencer# A tibble: 40 × 4
Werbekennzeichnung PW_TAEUSCHEN PW_UEBERZEUGEN Reaktanz
<dbl> <dbl> <dbl> <dbl>
1 0 5 3 5
2 0 4 3 4
3 0 4 3 3
4 0 4 3 3
5 0 4 2 3
# ℹ 35 more rows3.2 Regressionsbasierte Analyse
3.2.1 Bivariater Zusammenhang
Zunächst machen wir uns mit den relevanten Variablen vertraut und nutzen dafür die report_table()-Funktion.
d_zeitung |>
select(Zeitungsnutzungsdauer, PolWiss, PolInt) |>
report::report_table()Variable | n_Obs | Mean | SD | Median | MAD | Min | Max | Skewness | Kurtosis | percentage_Missing
--------------------------------------------------------------------------------------------------------------------
Zeitungsnutzungsdauer | 100 | 3.09 | 0.67 | 3.00 | 0.89 | 1.80 | 4.60 | 0.02 | -0.78 | 0.00
PolWiss | 100 | 3.47 | 0.69 | 3.67 | 0.49 | 1.00 | 5.00 | -0.67 | 0.76 | 0.00
PolInt | 100 | 3.20 | 0.72 | 3.33 | 0.99 | 1.67 | 5.00 | -0.07 | -0.90 | 0.00Als nächstes schätzen wir ein einfaches bivariates Regressionmodell, um den (totalen) Effekt von Zeitungsnutzungsdauer auf pol. Wissen zu testen.
model_total <- lm(PolWiss ~ Zeitungsnutzungsdauer, data = d_zeitung)
report::report_table(model_total)Parameter | Coefficient | 95% CI | t(98) | p | Std. Coef. | Std. Coef. 95% CI | Fit
-------------------------------------------------------------------------------------------------------------
(Intercept) | 2.60 | [1.98, 3.23] | 8.25 | < .001 | -4.18e-16 | [-0.19, 0.19] |
Zeitungsnutzungsdauer | 0.28 | [0.08, 0.48] | 2.81 | 0.006 | 0.27 | [ 0.08, 0.47] |
| | | | | | |
AIC | | | | | | | 207.30
AICc | | | | | | | 207.55
BIC | | | | | | | 215.12
R2 | | | | | | | 0.07
R2 (adj.) | | | | | | | 0.06
Sigma | | | | | | | 0.67Der Zusammenhang ist positiv und statistisch signifikant, d.h. eine stärkere Zeitungsnutzung hängt mit mehr politischem Wissen zusammen.
3.2.2 Mediationanalyse mit Regressionen
Wir gehen im Folgenden davon aus, dass der (positive) Effekt des Zeitungslesens auf pol. Wissen zumindest teilweise vom pol. Interesse mediiert wird. Anders formuliert: Zeitunglesen sollte politisches Interesse steigern, das wiederum zum mehr politischem Wissen führt (z.B. weil relevante Informationen besser erinnert werden).

Um die in der Abbildung dargestellte Mediationshypothese mit politischem Interesse als Mediatorvariable zu prüfen, gibt es verschiedene Möglichkeiten:
- Wir schätzen die beiden Regressionsmodelle einzeln mit der bekannten
lm-Funktion und berechnen dann den indirekten Effekt samt Konfidenzintervall mit demmediation-Paket. - Wir schätzen ein lineares Pfad- oder Strukturgleichungsmodell, in dem alle dargestellten Zusammenhänge simultan geschätzt werden. Hierfür benötigen wir das
lavaan-Paket.
Beide Varianten kommen zu (fast) identischen Ergebnissen, haben aber spezifische Vor- und Nachteile. Zunächst schätzen wir die beiden Teilmodelle, die per Konvention als a bzw. bc-Regressionen bezeichnet werden.
model_a <- lm(PolInt ~ Zeitungsnutzungsdauer, data = d_zeitung)
report::report_table(model_a)Parameter | Coefficient | 95% CI | t(98) | p | Std. Coef. | Std. Coef. 95% CI | Fit
-------------------------------------------------------------------------------------------------------------
(Intercept) | 1.94 | [1.31, 2.57] | 6.09 | < .001 | -4.54e-16 | [-0.18, 0.18] |
Zeitungsnutzungsdauer | 0.41 | [0.21, 0.61] | 4.05 | < .001 | 0.38 | [ 0.19, 0.56] |
| | | | | | |
AIC | | | | | | | 208.89
AICc | | | | | | | 209.14
BIC | | | | | | | 216.71
R2 | | | | | | | 0.14
R2 (adj.) | | | | | | | 0.13
Sigma | | | | | | | 0.67Es gibt einen positiven, stat. signifikanten Zusammenhang zwischen Zeitungsnutzung und pol. Interesse, d.h. der \(a\)-Pfad ist signifikant.
model_bc <- lm(PolWiss ~ Zeitungsnutzungsdauer + PolInt, data = d_zeitung)
report::report_table(model_bc)Parameter | Coefficient | 95% CI | t(97) | p | Std. Coef. | Std. Coef. 95% CI | Fit
--------------------------------------------------------------------------------------------------------------
(Intercept) | 1.85 | [ 1.17, 2.53] | 5.39 | < .001 | -2.32e-16 | [-0.18, 0.18] |
Zeitungsnutzungsdauer | 0.12 | [-0.08, 0.32] | 1.22 | 0.227 | 0.12 | [-0.07, 0.31] |
PolInt | 0.39 | [ 0.21, 0.57] | 4.21 | < .001 | 0.41 | [ 0.22, 0.60] |
| | | | | | |
AIC | | | | | | | 192.53
AICc | | | | | | | 192.96
BIC | | | | | | | 202.95
R2 | | | | | | | 0.22
R2 (adj.) | | | | | | | 0.20
Sigma | | | | | | | 0.62Es gibt außerdem einen positiven, statistisch signifikanten Zusammenhang zwischen politischem Interesse und politischem Wissen, der \(b\)-Pfad, während der verbleibende direkte Effekt \(c'\) nicht statistisch signifikant ist.
Da \(a\) und \(b\)-Pfade signifikant sind (joint significance), können wir die Mediationshyptothese annehmen. In der Praxis wird darüber hinaus jedoch häufig der indirekte Effekt \(ab\) selbst noch quantifiziert, d.h das Produkt aus \(a\) und \(b\)-Koeffizienten.
3.2.3 Indirekter Effekt
Während man die Punktschätzer für \(ab\) einfach ausmultiplizieren kann, ist die inferenzstatisches Prüfung bzw. Berechnung des Konfidenzintervalls nicht ganz so leicht. Hayes und Scharkow (2013) listen eine Reihe von Verfahren auf, von denen Bootstrapping mit Perzentil-Intervall empfohlen wird. Dies könnte man manuell in R schätzen, es gibt aber mit der mediate-Funktion eine komfortablere Lösung. Als Funktionsargumente werden, das \(a\)-Regressionsmodell, das \(bc\)-Regressionsmodell, der Name der \(X\)-Variable und der Name der Mediatorvariable \(M\) übergeben. Über boot = TRUE fordern wir ein Bootstrap-basiertes Konfidenzintervall an. Das Ergebnis des Aufrufs wird dann über summary() zusammengefasst.
mediation::mediate(model_a, model_bc,
treat = "Zeitungsnutzungsdauer",
mediator = "PolInt",
boot = TRUE
) |>
summary()
Causal Mediation Analysis
Nonparametric Bootstrap Confidence Intervals with the Percentile Method
Estimate 95% CI Lower 95% CI Upper p-value
ACME 0.1593 0.0561 0.29 <2e-16 ***
ADE 0.1214 -0.1093 0.31 0.282
Total Effect 0.2807 0.0712 0.47 0.016 *
Prop. Mediated 0.5674 0.1896 1.94 0.016 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Sample Size Used: 100
Simulations: 1000 Der indirekte Effekt (ACME) ist positiv, das 95%-Konfidenzintervall enthält nicht die Null, d.h. der Effekt ist statistisch signfikant. Zusätzlich werden der direkte Effekt \(c'\) (ADE), der totale Effekt (siehe unser bivariate Regression oben) sowie das Verhältnis von indirektem zu totalem Effekt (Prop. Mediated) ausgegeben. Insgesamt zeigt sich auch hier, dass wir die Mediationshypothese annehmen können.
3.3 Pfadanalyse
Alternativ zu Einzelregressionen kann man über Strukturgleichungsmodelle (fast) beliebig komplexe Zusammenhänge simultan schätzen. Hierfür verwenden wir das lavaan-Paket, das eine recht einfache Spezifikationssyntax hat.
3.3.1 Pfadmodelle
Die Schätzung von Pfadmodellen mit lavaan besteht immer aus zwei Teilschritten: Modellspezifikation und Modellschätzung. Die Spezifikation besteht darin, dass wir in einem character-Objekt einen oder mehrere Pfade im Modell beschreiben. In unserem Fall sind es Regressionsmodelle, die exakt die gleiche Form haben, wie die Formel im lm-Aufruf. Wir schreiben beide Regressionsformeln nacheinander in das Modell.
simple_model <- "
PolInt ~ Zeitungsnutzungsdauer
PolWiss ~ PolInt + Zeitungsnutzungsdauer
"Nach der Spezifikation geschieht erst einmal nichts, da wir nur ein Objekt mit etwas Text angelegt haben. Geschätzt wird das Modell erst mit dem Aufruf der sem()-Funktion. Diese bekommt als erstes Argument unser spezifiziertes Modell, als zweites die Daten, mit denen das Modell geschätz werden sollen. Über die summary()-Funktion bekommen wir eine sehr ausführliche Zusammenfassung der Schätzung. Entscheidend ist zunächst, dass das Modell erfolgreich geschätzt wurde (Zeile 1) sowie die Schätzer für die Regressionskoeffizienten. Diese entsprechen exakt den mit lm() geschätzten Koeffizienten von oben.
results_simple <- lavaan::sem(model = simple_model, data = d_zeitung)
summary(results_simple, standardized = TRUE, rsquare = TRUE)lavaan 0.6-18 ended normally after 1 iteration
Estimator ML
Optimization method NLMINB
Number of model parameters 5
Number of observations 100
Model Test User Model:
Test statistic 0.000
Degrees of freedom 0
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Regressions:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
PolInt ~
Zetngsntzngsdr 0.409 0.100 4.095 0.000 0.409 0.379
PolWiss ~
PolInt 0.390 0.091 4.273 0.000 0.390 0.408
Zetngsntzngsdr 0.121 0.098 1.235 0.217 0.121 0.118
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.PolInt 0.445 0.063 7.071 0.000 0.445 0.856
.PolWiss 0.371 0.052 7.071 0.000 0.371 0.783
R-Square:
Estimate
PolInt 0.144
PolWiss 0.2173.3.2 Einfache Mediation
Für die Mediationsanalyse machen wir uns die Möglichkeit zunutze, in der Modellspezifikation bestimmte Parameter (oder Pfade) benennen zu können, etwa den \(a\), \(b\) und \(c'\) Parameter aus dem Mediationsmodell.
Im unteren Teil der Spezifikation definieren wir dann den indirekten (\(a * b\)) und totalen Effekt (\(ab + c\)) aus den benannten Modellparametern. Diese werden bei der Schätzung ebenfalls berücksichtigt, inklusive Standardfehler bzw. Konfidenzintervallen. Wir bekommen also alle relevanten Modellergebnisse auf einmal geliefert.
med_model <- "
# Regressionen
PolInt ~ a * Zeitungsnutzungsdauer
PolWiss ~ b * PolInt + c * Zeitungsnutzungsdauer
# abgeleitete Parameter
indirect := a * b
total := indirect + c
prop_mediated := indirect / total
"Der Modellaufruf ist wie im obigen Beispiel, jedoch wollen wir anstelle (falscher) asymptotischer Standardfehler und Konfidenzintervalle wiederum Bootstrap-basierte erhalten.
results_med <- lavaan::sem(
model = med_model, data = d_zeitung,
se = "bootstrap", bootstrap = 1000
)
summary(results_med, standardized = TRUE, rsquare = TRUE)lavaan 0.6-18 ended normally after 1 iteration
Estimator ML
Optimization method NLMINB
Number of model parameters 5
Number of observations 100
Model Test User Model:
Test statistic 0.000
Degrees of freedom 0
Parameter Estimates:
Standard errors Bootstrap
Number of requested bootstrap draws 1000
Number of successful bootstrap draws 1000
Regressions:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
PolInt ~
Ztngsntzng (a) 0.409 0.099 4.142 0.000 0.409 0.379
PolWiss ~
PolInt (b) 0.390 0.112 3.495 0.000 0.390 0.408
Ztngsntzng (c) 0.121 0.118 1.033 0.302 0.121 0.118
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.PolInt 0.445 0.051 8.657 0.000 0.445 0.856
.PolWiss 0.371 0.059 6.250 0.000 0.371 0.783
R-Square:
Estimate
PolInt 0.144
PolWiss 0.217
Defined Parameters:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
indirect 0.159 0.058 2.743 0.006 0.159 0.155
total 0.281 0.113 2.486 0.013 0.281 0.273
prop_mediated 0.567 3.485 0.163 0.871 0.567 0.567Da uns nur die Regressions- und definierten Koeffizienten interessieren, nutzen wir die report_table()-Funktion und filtern alle anderen Modellparameter heraus.
report::report_table(results_med) |>
filter(Coefficient != "")Parameter | Coefficient | 95% CI | z | p | Label | Component | Fit
----------------------------------------------------------------------------------------------------------------
PolInt ~ Zeitungsnutzungsdauer | 0.41 | [ 0.20, 0.59] | 4.14 | < .001 | a | Regression |
PolWiss ~ PolInt | 0.39 | [ 0.18, 0.61] | 3.49 | < .001 | b | Regression |
PolWiss ~ Zeitungsnutzungsdauer | 0.12 | [-0.12, 0.33] | 1.03 | 0.302 | c | Regression |
indirect := a*b | 0.16 | [ 0.05, 0.29] | 2.74 | 0.006 | indirect | Defined |
total := indirect+c | 0.28 | [ 0.03, 0.48] | 2.49 | 0.013 | total | Defined |
prop_mediated := indirect/total | 0.57 | [ 0.17, 2.35] | 0.16 | 0.871 | prop_mediated | Defined | Jetzt erhalten wir alle relevanten Modellergebnisse in einem Schritt, mit fast identischen Ergebnissen im Vergleich zu den einzelnen Regressionen oben.
3.3.3 Multiple Mediation
Als zweites Beispiel schätzen wir ein Mediationsmodell zum Einfluss von Werbekennzeichnungen bei Influencern. Zunächst machen wir uns mit den relevanten Variablen vertraut, bevor wir das Pfadmodell schätzen.
d_influencer |>
report::report_table()Variable | n_Obs | Mean | SD | Median | MAD | Min | Max | Skewness | Kurtosis | n_Missing
--------------------------------------------------------------------------------------------------------
Werbekennzeichnung | 40 | 0.50 | 0.51 | 0.50 | 0.74 | 0.00 | 1.00 | 0.00 | -2.11 | 0
PW_TAEUSCHEN | 40 | 3.10 | 1.32 | 3.00 | 1.48 | 1.00 | 5.00 | -0.19 | -1.11 | 0
PW_UEBERZEUGEN | 40 | 3.12 | 1.07 | 3.00 | 1.48 | 1.00 | 5.00 | 0.14 | -0.43 | 0
Reaktanz | 40 | 3.30 | 0.88 | 3.00 | 1.48 | 2.00 | 5.00 | 0.30 | -0.48 | 0Pfadmodelle haben den Vorteil, dass sie (fast) beliebig erweiterbar sind, d.h. wir können auch komplexere Modelle schätzen, etwa eine parallele multiple Mediation, wie in der Abbildung dargestellt.
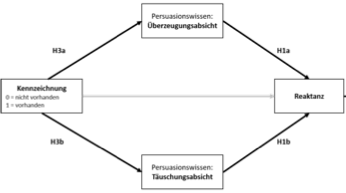
Das multiple Mediationsmodell hat jeweils zwei \(a\) und \(b\)-Pfade (d.h. drei Regressionsgleichungen). Üblicherweise wird auch der Zusammenhang zwischen den beiden Mediatorvariablen geschätzt (mit ~~ spezifiziert), weil es plausibel ist, dass diese auch zusammenhängen. Anschließend werden zwei indirekte und ein totaler Effekt definiert und das Modell dann geschätzt.
multmed_model <- "
# Regressionen
PW_UEBERZEUGEN ~ a1 * Werbekennzeichnung
PW_TAEUSCHEN ~ a2 * Werbekennzeichnung
Reaktanz ~ b1 * PW_UEBERZEUGEN + b2 * PW_TAEUSCHEN + c * Werbekennzeichnung
# Korrelation der Mediatoren
PW_UEBERZEUGEN ~~ PW_TAEUSCHEN
# abgeleitete Parameter
indirect1 := a1 * b1
indirect2 := a2 * b2
total := indirect1 + indirect2 + c
"
results_multmed <- lavaan::sem(
model = multmed_model, data = d_influencer,
se = "bootstrap", bootstrap = 1000
)
summary(results_multmed, standardized = TRUE, rsquare = TRUE)lavaan 0.6-18 ended normally after 9 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 9
Number of observations 40
Model Test User Model:
Test statistic 0.000
Degrees of freedom 0
Parameter Estimates:
Standard errors Bootstrap
Number of requested bootstrap draws 1000
Number of successful bootstrap draws 998
Regressions:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
PW_UEBERZEUGEN ~
Wrbknnzch (a1) 1.050 0.297 3.531 0.000 1.050 0.498
PW_TAEUSCHEN ~
Wrbknnzch (a2) -1.300 0.365 -3.558 0.000 -1.300 -0.500
Reaktanz ~
PW_UEBERZ (b1) 0.422 0.158 2.665 0.008 0.422 0.509
PW_TAEUSC (b2) 0.250 0.120 2.086 0.037 0.250 0.373
Wrbknnzch (c) -0.318 0.282 -1.129 0.259 -0.318 -0.182
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.PW_UEBERZEUGEN ~~
.PW_TAEUSCHEN -0.146 0.153 -0.954 0.340 -0.146 -0.142
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.PW_UEBERZEUGEN 0.834 0.183 4.558 0.000 0.834 0.752
.PW_TAEUSCHEN 1.268 0.260 4.878 0.000 1.268 0.750
.Reaktanz 0.553 0.117 4.740 0.000 0.553 0.728
R-Square:
Estimate
PW_UEBERZEUGEN 0.248
PW_TAEUSCHEN 0.250
Reaktanz 0.272
Defined Parameters:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
indirect1 0.443 0.189 2.346 0.019 0.443 0.254
indirect2 -0.325 0.177 -1.837 0.066 -0.325 -0.186
total -0.200 0.280 -0.713 0.476 -0.200 -0.115Der Output ist lediglich etwas länger als zuvor, aber die relevanten Koeffizienten finden sich an denselben Stellen. Auch hier können wir den Output auf die notwendigen Angaben filtern.
report_table(results_multmed) |>
filter(Coefficient != "")Parameter | Coefficient | 95% CI | z | p | Label | Component | Fit
-------------------------------------------------------------------------------------------------------------------
PW_UEBERZEUGEN ~ Werbekennzeichnung | 1.05 | [ 0.45, 1.66] | 3.53 | < .001 | a1 | Regression |
PW_TAEUSCHEN ~ Werbekennzeichnung | -1.30 | [-2.00, -0.60] | -3.56 | < .001 | a2 | Regression |
Reaktanz ~ PW_UEBERZEUGEN | 0.42 | [ 0.12, 0.73] | 2.67 | 0.008 | b1 | Regression |
Reaktanz ~ PW_TAEUSCHEN | 0.25 | [ 0.00, 0.47] | 2.09 | 0.037 | b2 | Regression |
Reaktanz ~ Werbekennzeichnung | -0.32 | [-0.88, 0.24] | -1.13 | 0.259 | c | Regression |
PW_UEBERZEUGEN ~~ PW_TAEUSCHEN | -0.15 | [-0.44, 0.16] | -0.95 | 0.340 | | Correlation |
indirect1 := a1*b1 | 0.44 | [ 0.12, 0.85] | 2.35 | 0.019 | indirect1 | Defined |
indirect2 := a2*b2 | -0.32 | [-0.67, 0.01] | -1.84 | 0.066 | indirect2 | Defined |
total := indirect1+indirect2+c | -0.20 | [-0.78, 0.31] | -0.71 | 0.476 | total | Defined | Beide indirekten Effekte sind statistisch signifikant, aber gegenläufig, was häufig als sog. Suppressionseffekt interpretiert wird.
Achtung, bei genauerer Betrachtung des totalen Effekts stellen wir fest, dass dieser gar nicht statistisch signifikant ist, d.h. wir haben keinen Beleg dafür, dass die Werbekennzeichnung überhaupt die Reaktanz der Proband:innen beeinflusst hat. Dies sollte auch und erst recht bei der kausalen (Über-) Interpretation komplexer Mediationsmodelle berücksichtigt werden, vor allem, wenn die Mediatoren nicht experimentell manipuliert wurden.
3.4 Glossar
| Funktion | Definition |
|---|---|
| lavaan::sem | Pfadmodelle schätzen |
| mediation::mediate | Mediationseffekte analysieren |
3.5 Hausaufgabe
Gegeben sei folgenden Hypothese:
„Je mehr Pornografie eine Person konsumiert, desto eher ist sie untreu. Dieser Zusammenhang wird vom Commitment für die Beziehung mediiert: Je höher der Pornografiekonsum ausfällt, desto geringer ist das Committment, und je geringer das Committment ist, desto häufiger ist einer Person untreu.»
Testen Sie diese Mediationshypothese mit dem Datensatz lambert.sav.