8 Logistische Regression
Beispielanalyse
Was sagt vorher, wer Opfer von Cybermobbing wird?
8.1 Pakete und Daten laden
Wir laden die üblichen Pakete sowie das marginaleffects-Paket, das es uns ermöglicht, Modellvorhersagen für die Interpretation der Koeffizienten zu nutzen.
library(marginaleffects)
library(report)
library(tidyverse)
theme_set(theme_minimal())Anschließend laden wir die Daten, die in Form einer SPSS-Datei vorliegen. Der Datensatz enthält sechs Variablen. Für die nachfolgende Analyse nutzen wir die Outcome-Variable cbvictim_gen, das Geschlecht gender und die Internutzung internetuse. Die Outcome-Variable ist dichotom (0/1), während es sich bei den Prädiktoren um eine nominalskalierte (Geschlecht) und eine metrische (Internetnutzung pro Tag) Variable handelt.
festl13 <- haven::read_sav("data/Festl13.sav") |>
mutate(gender = as_factor(gender)) |>
haven::zap_labels()
festl13# A tibble: 275 × 6
cbbully_gen cbvictim_gen age gender internetuse class
<dbl> <dbl> <dbl> <fct> <dbl> <chr>
1 0 0 13 male 1 G7a
2 0 0 13 male 2 G7a
3 0 0 13 male 0.2 G7a
4 0 0 13 male 0.75 G7a
5 0 0 13 male 0.5 G7a
# ℹ 270 more rows8.2 Deskriptivstatistik
Zunächst berechnen wir univariate Statistiken für unsere Outcome-Variable. Der Mittelwert entspricht bei dichotomen Variablen dem Anteil der Fälle mit der Ausprägung 1.
festl13 |>
select(cbvictim_gen) |>
report::report_table()Variable | n_Obs | Mean | SD | Median | MAD | Min | Max | Skewness | Kurtosis | percentage_Missing
-----------------------------------------------------------------------------------------------------------
cbvictim_gen | 275 | 0.11 | 0.31 | 0.00 | 0.00 | 0.00 | 1.00 | 2.58 | 4.71 | 0.008.3 Nullmodell
Für die logistische Regression bietet es sich an, zunächst mit einem Nullmodell (auch intercept-only model) zu starten. In R kann dies mit einer 1 anstatt einer Variablenbezeichnungen in der Formel umgesetzt werden. Zudem müssen wir im Funktionsargument family angeben, dass es sich um eine logistische Regression handelt, in dem wir dort den Wert binomial eintragen.
m0 <- glm(cbvictim_gen ~ 1, data = festl13, family = binomial)
report::report_table(m0)Parameter | Coefficient | 95% CI | z | p | Std. Coef. | Std. Coef. 95% CI | Fit
------------------------------------------------------------------------------------------------------
(Intercept) | -2.14 | [-2.52, -1.75] | -10.89 | < .001 | -2.14 | [-2.52, -1.75] |
| | | | | | |
AIC | | | | | | | 187.30
AICc | | | | | | | 187.31
BIC | | | | | | | 190.91
Tjur's R2 | | | | | | | 0.00
Sigma | | | | | | | 1.00
Log_loss | | | | | | | 0.34Der Intercept lässt sich durch die sog. Inverse Logit Funktion (in R plogis()) in eine Baseline-Wahrscheinlichkeit umrechnen. Dieser Wert sollte im Nullmodel mit dem Anteil der Fälle mit der Ausprägung 1 übereinstimmen (siehe oben), weshalb wir den Wert zum Vergleich ebenfalls mit round() runden.
plogis(-2.14)[1] 0.1052694round(plogis(-2.14), 2)[1] 0.118.4 Bivariate logistische Regression
8.4.1 Prädiktor Geschlecht
Wir beginnen unsere Analyse mit einer einfachen bivariaten logistischen Regression. Die von R berechneten Koffezienten sind sogenannte Logits (auch Log-Odds). Eine direkte Interpretation dieser Koeffizienten ist schwer, weshalb meist nur Signifikanz und Vorzeichen betrachtet werden.
m1_gender <- glm(cbvictim_gen ~ gender, festl13, family = binomial(link = "logit"))
report::report_table(m1_gender)Parameter | Coefficient | 95% CI | z | p | Std. Coef. | Std. Coef. 95% CI | Fit
---------------------------------------------------------------------------------------------------------
(Intercept) | -2.48 | [-3.13, -1.94] | -8.27 | < .001 | -2.48 | [-3.13, -1.94] |
gender [female] | 0.69 | [-0.08, 1.50] | 1.74 | 0.082 | 0.69 | [-0.08, 1.50] |
| | | | | | |
AIC | | | | | | | 186.22
AICc | | | | | | | 186.26
BIC | | | | | | | 193.45
Tjur's R2 | | | | | | | 0.01
Sigma | | | | | | | 1.00
Log_loss | | | | | | | 0.33Ergebnis: Es besteht ein positiver, aber nicht statistisch signifikanter Zusammenhang zwischen Geschlecht und dem Risiko, Opfer von Cybermobbing zu werden.
8.4.2 Average Marginal Effects
Die Interpretation der Vorzeichen und Signifikanz ist eher unbefriedigend, da uns dieses Vorgehen nicht wirklich hilft, die Größe des Effekts greifbar zu machen. Eine bessere Herangehensweise ist die Berechnung von Average Marginal Effects (AME). Die Kernidee ist, für jeden Wert der Prädiktorvariable in der Stichprobe den Anstieg in der Logit-Funktion der Outcome-Variable zu berechnen, und davon über die gesamte Stichprobe den Mittelwert zu errechnen. Dieser lässt sich als durchschnittliche Veränderung in der Wahrscheinlichkeit \(P(Y=1)\) über alle Fälle in der Stichprobe interpretieren. Dazu können wir die Funktionen aus dem marginaleffects-Paket nutzen. Mit der Funktion avg_comparisons vergleichen wir die durchschnittliche Veränderung in der Wahrscheinlichkeit von Jungen und Mädchen Opfer von Cybermobbing zu werden.
marginaleffects::avg_comparisons(m1_gender) |>
as_tibble()# A tibble: 1 × 12
term contrast estimate std.error statistic p.value s.value conf.low conf.high
<chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 gend… mean(fe… 0.0659 0.0385 1.71 0.0870 3.52 -0.00957 0.141
# ℹ 3 more variables: predicted_lo <dbl>, predicted_hi <dbl>, predicted <dbl>Da Wahrscheinlichkeiten als Prozentangabe interpretiert werden können, ist die Ergebnisinterpretation denkbar einfach.
Ergebnis: Mädchen besitzen eine 6 Prozentpunkte höhere durchschnittliche Wahrscheinlichkeit, Opfer von Cybermobbing zu werden. Der Unterschied ist natürlich auch hier nicht statistisch signifikant, weshalb wir ihn nicht weiter interpretieren.
8.4.3 Vorhergesagte Wahrscheinlichkeiten
Wir können das Modell auch nutzen, um uns die AME für beide Geschlecht mit der Funktion avg_predictions() auszugeben. Ziehen wir die beiden vorhergesagten Wahrscheinlichkeiten in der Spalte estimate voneinander ab, erhalten wir den gleichen Wert wie zuvor mit avg_comparisons().
preds_gender <- marginaleffects::avg_predictions(m1_gender, variables = "gender") |>
as_tibble()
preds_gender# A tibble: 2 × 6
gender estimate p.value s.value conf.low conf.high
<fct> <dbl> <dbl> <dbl> <dbl> <dbl>
1 male 0.0769 1.34e-16 52.7 0.0442 0.131
2 female 0.143 7.94e-12 36.9 0.0907 0.2188.4.4 Visualisierte Vorhersagen
Mit ggplot() können wir uns die vorhergesagten Wahrscheinlichkeiten des Modells grafisch darstellen.
preds_gender |>
ggplot(aes(x = gender, y = estimate, ymin = conf.low, ymax = conf.high)) +
geom_pointrange() +
labs(y = "Predicted Probability of Cybervictimization", x = "Gender")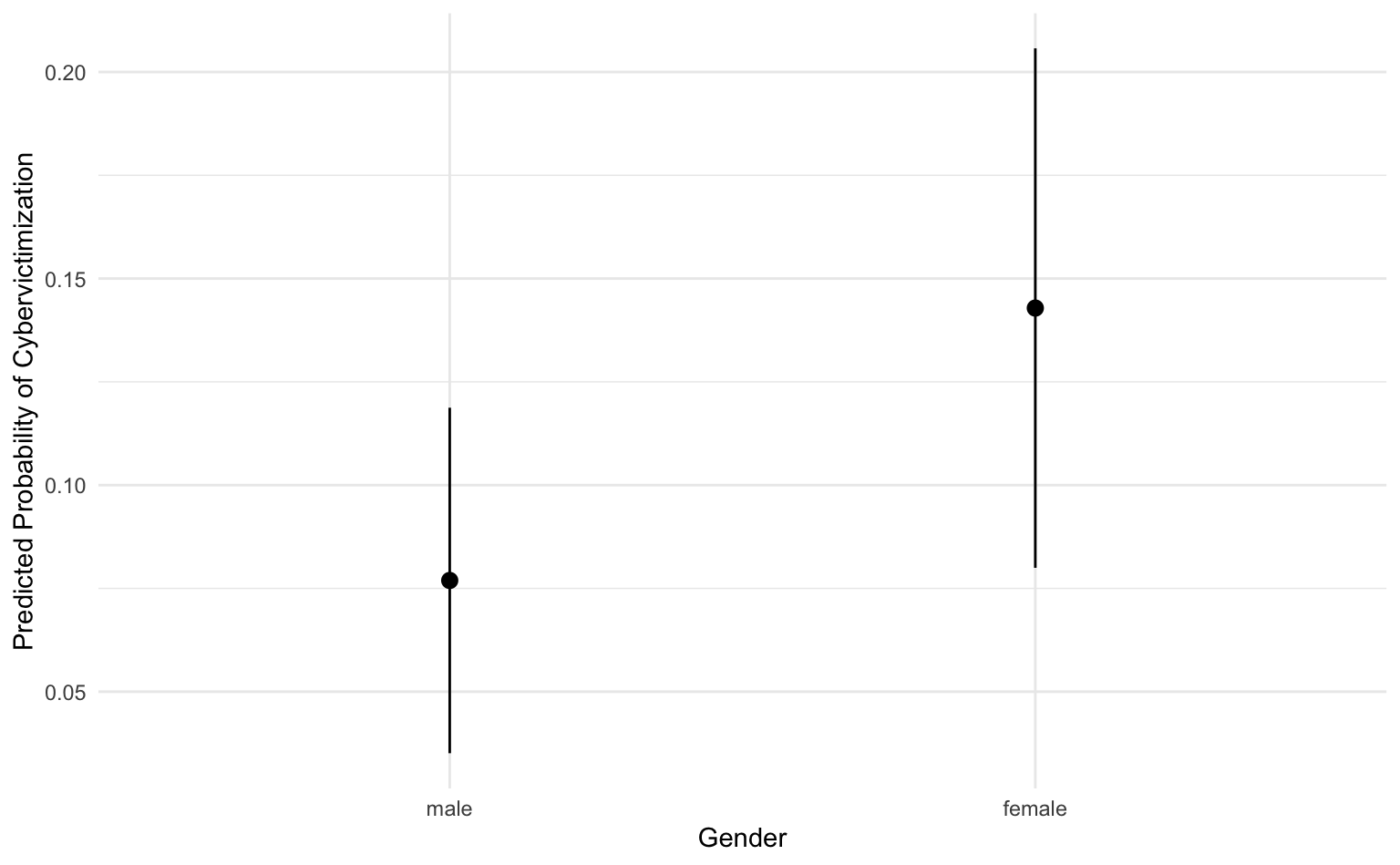
8.5 Multiple logistische Regression
8.5.1 Prädiktoren Geschlecht und Internetnutzung
Wie bei der linearen Regression können wir auch für die logistische Regression mehrere Prädiktoren verwenden. Das nachfolgende Modell enthält neben dem Geschlecht auch noch die tägliche Internetnutzung in Stunden. Die Interpretation ist analog zum bivariaten Fall.
m2_gender_internet <- glm(cbvictim_gen ~ gender + internetuse, data = festl13, family = binomial)
report_table(m2_gender_internet)Parameter | Coefficient | 95% CI | z | p | Std. Coef. | Std. Coef. 95% CI | Fit
---------------------------------------------------------------------------------------------------------
(Intercept) | -2.98 | [-3.82, -2.23] | -7.41 | < .001 | -2.56 | [-3.23, -2.00] |
gender [female] | 0.76 | [-0.02, 1.58] | 1.88 | 0.060 | 0.76 | [-0.02, 1.58] |
internetuse | 0.19 | [ 0.00, 0.37] | 2.10 | 0.036 | 0.34 | [ 0.00, 0.65] |
| | | | | | |
AIC | | | | | | | 184.27
AICc | | | | | | | 184.36
BIC | | | | | | | 195.12
Tjur's R2 | | | | | | | 0.03
Sigma | | | | | | | 1.00
Log_loss | | | | | | | 0.32Der Koeffizient für die Internetnutzung ist positiv und signifikant. Allerdings ist die erklärte Varianz (Pseudo \(R^2\)) nach wie vor eher gering (\(R^2\) = .03). Die anderen Koeffizienten ändern sich durch die zusätzliche unabhängige Variable Internetnutzung kaum.
8.5.2 Average Marginal Effects
Wie für den bivariaten Fall lassen sich auch für die multiple logistische Regression Average Marginal Effects berechnen und visualisieren.
marginaleffects::avg_comparisons(m2_gender_internet) |>
as_tibble()# A tibble: 2 × 12
term contrast estimate std.error statistic p.value s.value conf.low conf.high
<chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 gend… mean(fe… 0.0712 0.0385 1.85 0.0647 3.95 -4.35e-3 0.147
2 inte… mean(+1) 0.0187 0.00946 1.98 0.0482 4.37 1.47e-4 0.0372
# ℹ 3 more variables: predicted_lo <dbl>, predicted_hi <dbl>, predicted <dbl>Das Ergebnis von avg_comparisons zeigt uns, dass eine zusätzliche Stunde im Internet die durchschnittliche vorhergesagte Wahrscheinlichkeit, Opfer von Cybermobbing zu werden, um 2 Prozentpunkte erhöht.
8.5.3 Vorhergesagte Wahrscheinlichkeiten
Mit der Funktion avg_predictions können wir auch vorhergesagte Wahrscheinlichkeiten für unsere metrische Variable Internetnutzung berechnen.
preds_internet <- marginaleffects::avg_predictions(m2_gender_internet, variables = c("internetuse")) |>
as_tibble()
preds_internet# A tibble: 5 × 6
internetuse estimate p.value s.value conf.low conf.high
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 0 0.0659 1.59e-16 52.5 0.0362 0.117
2 1 0.0786 1.83e-21 68.9 0.0489 0.124
3 2 0.0936 1.03e-25 83.0 0.0633 0.136
4 3 0.111 1.58e-23 75.7 0.0767 0.158
5 13 0.456 8.52e- 1 0.232 0.114 0.844Wir erhalten die vorhergesagten Wahrscheinlichkeiten für null, eine, zwei, drei & dreizehn (!) Stunden Internetnutzung am Tag.
8.5.4 Visualisierte Vorhersagen
Die vorhergesagten Wahrscheinlichkeiten für diese vier Werte lassen sich auch wieder mit ggplot() darstellen.
preds_internet |>
ggplot(aes(
x = internetuse, y = estimate, ymin = conf.low, ymax = conf.high
)) +
geom_line() +
geom_ribbon(alpha = .1) +
labs(
x = "Internet use (hours/day)",
y = "Predicted probability of Cybervictimization",
)
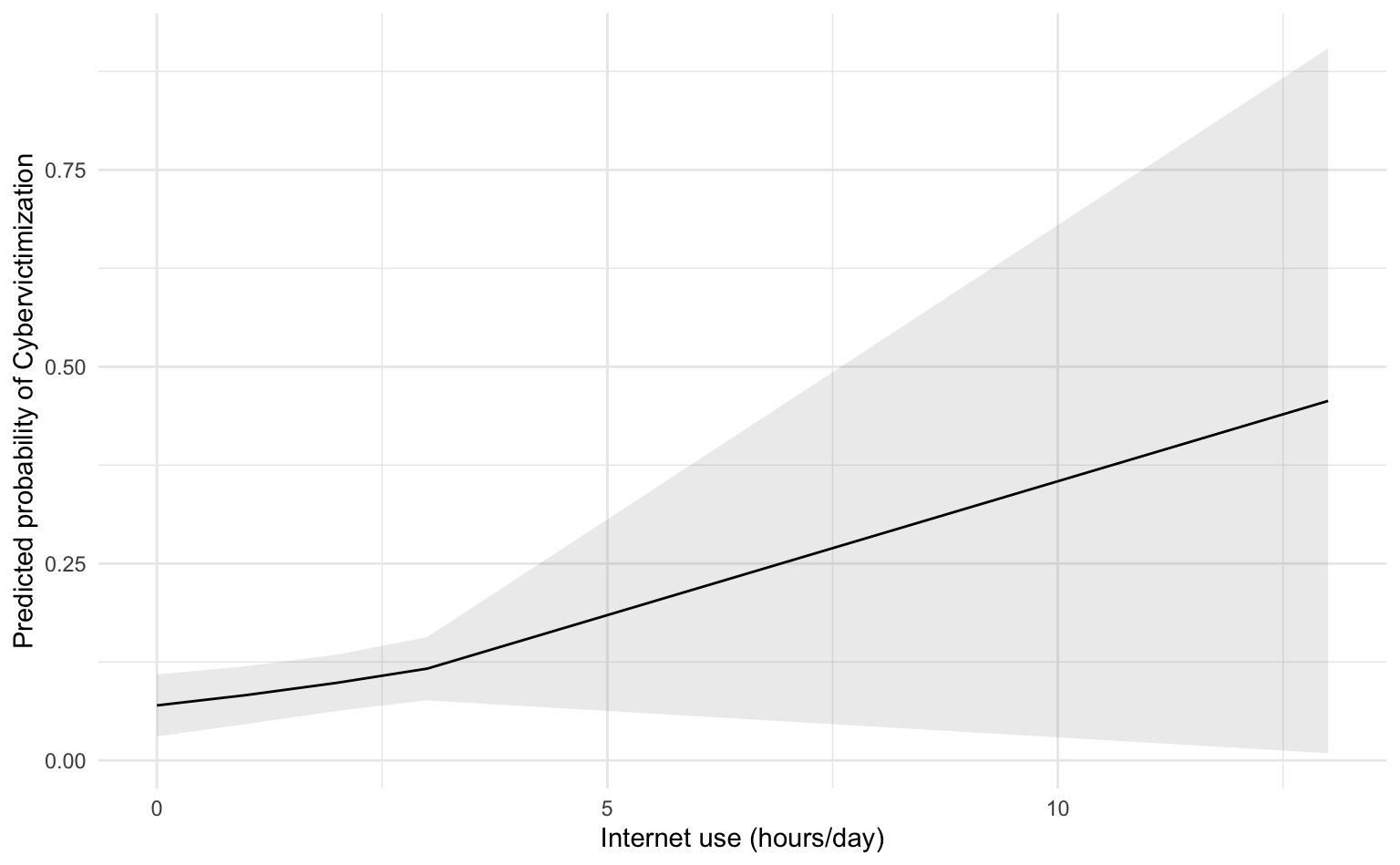
Auffallend ist, dass ein starker Anstieg der vorhergesagten Wahrscheinlichkeit erst für eine sehr exzessive Internetnutzung prognostiziert wird.