library(report)
library(tidyverse)
theme_set(theme_minimal())4 Multiple Regression
Beispielanalyse
Welche Variablen sagen politisches Wissen voraus?
4.1 Pakete und Daten laden
Zunächst laden wir die üblichen R-Pakete sowie die Daten von van Erkel & van Aelst (2021).
Wir wandeln die Variablen Eduction und Gender in kategorielle Variablen (factor) um, damit R deren Ausprägungen nicht als Zahlenwerte interpretiert.
vanerkel21 <- haven::read_sav("data/Vanerkel_Vanaelst_2021.sav") |>
mutate(
Education = as_factor(Education),
Gender = as_factor(Gender)
) |>
haven::zap_labels()
vanerkel21# A tibble: 993 × 74
StartDate_w3 EndDate_w3 Duration__in_seconds_w3 Gender Year_of_birtg Age
<date> <date> <dbl> <fct> <dbl> <dbl>
1 2019-04-09 2019-04-09 440 female 29 45
2 2019-04-09 2019-04-09 504 female 43 59
3 2019-04-06 2019-04-06 610 female 36 52
4 2019-04-03 2019-04-03 414 female 7 23
5 2019-04-09 2019-04-09 1274 female 7 23
# ℹ 988 more rows
# ℹ 68 more variables: Education <fct>, News_channels_w3_1 <dbl>,
# News_channels_w3_2 <dbl>, News_channels_w3_3 <dbl>,
# News_channels_w3_4 <dbl>, News_channels_w3_5 <dbl>,
# News_channels_w3_6 <dbl>, Political_interest <dbl>, StartDate_w4 <date>,
# EndDate_w4 <date>, Duration__in_seconds__w4 <dbl>,
# News_channels_w4_1 <dbl>, TV <dbl>, Newspaper <dbl>, Websites <dbl>, …Die relevante Outcome-Variable ist politisches Wissen PK, die wir nachfolgend genauer betrachten.
4.2 Deskriptive Statistik
vanerkel21 |>
select(PK) |>
report::report_table()Variable | n_Obs | Mean | SD | Median | MAD | Min | Max | Skewness
-----------------------------------------------------------------------
PK | 993 | 3.04 | 1.36 | 3.00 | 1.48 | 0.00 | 5.00 | -0.40
Variable | Kurtosis | percentage_Missing
----------------------------------------
PK | -0.47 | 0.00vanerkel21 |>
ggplot(aes(x = PK)) +
geom_histogram()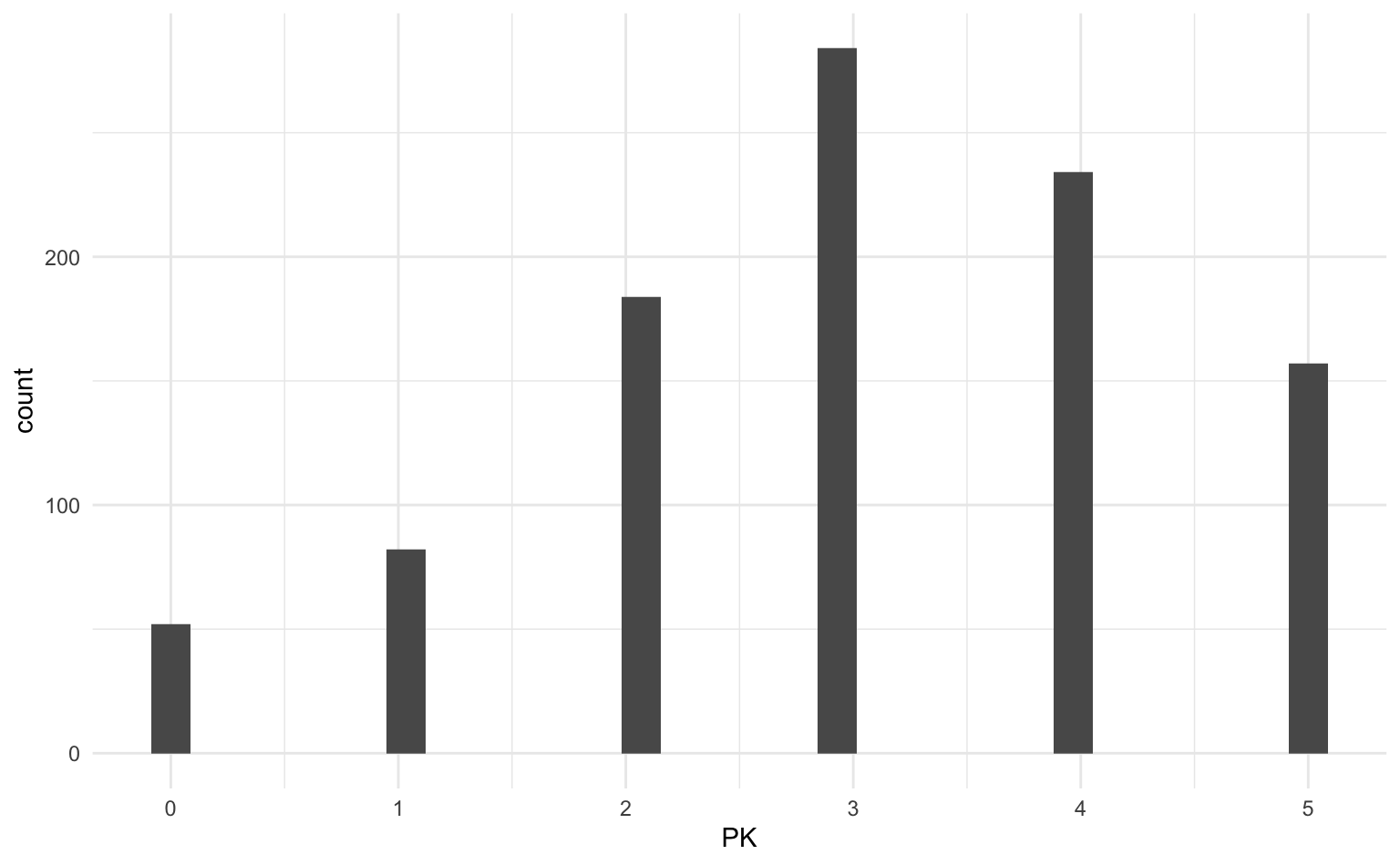
4.3 Modell 1: Nur Soziodemographie
Das erste Regressionsmodell enthält nur die soziodemographischen Variablen Geschlecht, Alter und Bildung.
m1_socdem <- lm(PK ~ Gender + Age + Education, data = vanerkel21)
report::report_table(m1_socdem)Parameter | Coefficient | 95% CI | t(988) | p
-------------------------------------------------------------------
(Intercept) | 1.35 | [ 0.96, 1.74] | 6.81 | < .001
Gender [female] | -0.73 | [-0.89, -0.58] | -9.23 | < .001
Age | 0.03 | [ 0.02, 0.03] | 9.46 | < .001
Education [Middle] | 0.51 | [ 0.27, 0.75] | 4.23 | < .001
Education [High] | 0.89 | [ 0.66, 1.13] | 7.43 | < .001
| | | |
AIC | | | |
AICc | | | |
BIC | | | |
R2 | | | |
R2 (adj.) | | | |
Sigma | | | |
Parameter | Std. Coef. | Std. Coef. 95% CI | Fit
-------------------------------------------------------------
(Intercept) | -0.20 | [-0.35, -0.04] |
Gender [female] | -0.54 | [-0.65, -0.42] |
Age | 0.28 | [ 0.22, 0.33] |
Education [Middle] | 0.38 | [ 0.20, 0.55] |
Education [High] | 0.66 | [ 0.48, 0.83] |
| | |
AIC | | | 3217.41
AICc | | | 3217.50
BIC | | | 3246.81
R2 | | | 0.20
R2 (adj.) | | | 0.20
Sigma | | | 1.22Alle Variablen sagen statistisch signifikant politisches Wissen voraus, und dies auch mit z.T. großen Effektstärken. Männliche und weibliche Befragte unterscheiden sich um einen dreiviertel Skalenpunkt, und auch die Unterschiede der mittleren und hohen Bildungsgruppe zu den Niedriggebildeten fallen sehr groß aus. Wegen der nicht-zentrierten Altersvariable lässt sich der Intercept-Term nicht sinnvoll interpretieren. Die Varianzaufklärung des Modells ist mit .20 relativ hoch.
4.4 Modell 2: plus Mediennutzung
Im zweiten Modell fügen wir die Mediennutzungsvariablen hinzu.
m2_media <- lm(PK ~ TV + Newspaper + Websites + Facebook + Twitter +
Gender + Age + Education, data = vanerkel21)
report::report_table(m2_media)Parameter | Coefficient | 95% CI | t(983) | p
-------------------------------------------------------------------
(Intercept) | 0.74 | [ 0.28, 1.20] | 3.18 | 0.002
TV | 0.14 | [ 0.08, 0.20] | 4.46 | < .001
Newspaper | 0.12 | [ 0.07, 0.17] | 4.91 | < .001
Websites | 0.12 | [ 0.07, 0.16] | 4.77 | < .001
Facebook | -0.07 | [-0.11, -0.03] | -3.29 | 0.001
Twitter | -0.07 | [-0.15, 0.01] | -1.81 | 0.070
Gender [female] | -0.63 | [-0.78, -0.48] | -8.21 | < .001
Age | 0.02 | [ 0.01, 0.02] | 6.23 | < .001
Education [Middle] | 0.39 | [ 0.16, 0.61] | 3.33 | < .001
Education [High] | 0.67 | [ 0.44, 0.90] | 5.69 | < .001
| | | |
AIC | | | |
AICc | | | |
BIC | | | |
R2 | | | |
R2 (adj.) | | | |
Sigma | | | |
Parameter | Std. Coef. | Std. Coef. 95% CI | Fit
-------------------------------------------------------------
(Intercept) | -0.12 | [-0.27, 0.03] |
TV | 0.14 | [ 0.08, 0.20] |
Newspaper | 0.15 | [ 0.09, 0.21] |
Websites | 0.15 | [ 0.09, 0.21] |
Facebook | -0.10 | [-0.16, -0.04] |
Twitter | -0.05 | [-0.11, 0.00] |
Gender [female] | -0.46 | [-0.57, -0.35] |
Age | 0.19 | [ 0.13, 0.25] |
Education [Middle] | 0.28 | [ 0.12, 0.45] |
Education [High] | 0.49 | [ 0.32, 0.66] |
| | |
AIC | | | 3114.06
AICc | | | 3114.32
BIC | | | 3167.96
R2 | | | 0.29
R2 (adj.) | | | 0.28
Sigma | | | 1.15Die Regressionskoeffizienten der Mediennutzungsvariablen sind alle positiv und statistisch signifikant (mit Ausnahme von Twitter), aber etwas kleiner als die soziodemographischen Variablen. Das adjustierte \(R^2\) ist auf .28 gestiegen.
4.5 Modellvergleich
Ob Modell 2 signifikant mehr Varianz im politischen Wissen erklären kann als Modell 1, zeigt der partielle F-Test, der mit der anova()-Funktion durchgeführt wird. Funktionsargumente sind die beiden Modelle, die verglichen werden sollen.
anova(m1_socdem, m2_media)Analysis of Variance Table
Model 1: PK ~ Gender + Age + Education
Model 2: PK ~ TV + Newspaper + Websites + Facebook + Twitter + Gender +
Age + Education
Res.Df RSS Df Sum of Sq F Pr(>F)
1 988 1466.8
2 983 1308.6 5 158.24 23.774 < 2.2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Die Residualvarianz von Modell 2 ist signifikant kleiner, bzw. die erklärte Varianz signifikant größer als bei Modell 1. Das Hinzunehmen der Mediennutzungsvariablen hat die Modellgüte also gesteigert.
4.6 Übungsaufgaben
- Fügen Sie die Variable
Political_interestals Prädiktor hinzu und interpretieren Sie das Ergebnis. - Vergleichen Sie zwei Modelle: eines mit traditioneller Mediennutzung und eines, in dem zusätzlich Facebook und Twitter-Nutzung als Prädiktor dienen. Tragen die Social-Media-Nutzungsvariablen zur Vorhersage des politischen Wissens bei?