library(lme4)
library(performance)
library(marginaleffects)
library(report)
library(tidyverse)
theme_set(theme_minimal())9 Multilevel-Regression
Beispielanalyse
Welche Facebook-Posts von Universitäten werden am meisten kommentiert?
9.1 Pakete und Daten laden
Wir beginnen mit unserem üblichen Setup. Hinzu kommen die Pakte lme4 und performance. lme4 benötigen wird für die Multilevel-Regression, während performance eine Funktion für die Berechnung des Intraclass Correlation Coefficient (ICC) enthält. Anschließend laden wir die Daten, die wieder in Form einer SPSS-Datei vorliegen.
faehnrich19 <- haven::read_sav("data/Faehnrich_2020.sav") |>
haven::zap_labels()
faehnrich19# A tibble: 10,807 × 20
id from_id uni created_time type status_type likes_count
<chr> <dbl> <chr> <dttm> <chr> <chr> <dbl>
1 102471088936_… 1.02e11 Colu… 2013-12-19 19:08:19 link shared_sto… 18
2 102471088936_… 1.02e11 Colu… 2013-03-08 15:48:25 video added_video 18
3 102471088936_… 1.02e11 Colu… 2013-03-05 21:33:03 link shared_sto… 19
4 102471088936_… 1.02e11 Colu… 2015-01-15 20:37:08 photo added_phot… 309
5 102471088936_… 1.02e11 Colu… 2013-12-02 19:40:34 link shared_sto… 27
# ℹ 10,802 more rows
# ℹ 13 more variables: comments_count <dbl>, shares_count <dbl>,
# timeofday <chr>, topic_research <dbl>, topic_teaching <dbl>,
# topic_awards <dbl>, topic_event <dbl>, topic_interact <dbl>,
# topic_self <dbl>, word_count <dbl>, year <dbl>, uni_us <dbl>,
# uni_fans <dbl>Multilevel-Modelle werden für die Analyse von hierarchisch geschachtelten Daten verwendet. Diese Datenstruktur liegt hier ebenfalls vor, da Facebook-Posts und deren Kommentare innerhalb von Facebook-Seiten gruppiert sind. Die Posts bilden damit eine Ebene unterhalb der Seiten, die von den Universitäten betrieben werden. Entsprechend liegen in unserem Datensatz 2 Ebenen vor: die Facebook-Seite der Universität (Level 2) und die Posts (Level 1).
9.2 Deskriptivstatistik
Wir betrachten zunächst die Level-2-Variable, in dem wir uns die Anzahl der Posts pro Universität in unserer Stichprobe ausgeben lassen.
count(faehnrich19, uni)# A tibble: 42 × 2
uni n
<chr> <int>
1 Columbia U 579
2 Cornell U 438
3 Duke U 333
4 Harvard U 221
5 Imperial College London 196
# ℹ 37 more rowsWie bei allen Analysen lohnt sich auch bei Mutlilevel-Modellen ein Blick auf die Verteilung der Outcome-Variable, in diesem Fall die Anzahl Kommentare pro Post.
faehnrich19 |>
select(comments_count) |>
report::report_sample()# Descriptive Statistics
Variable | Summary
----------------------------------------
Mean comments_count (SD) | 12.15 (36.46)Ein Blick in das Histogram verrät, dass die Variable eine starke rechtsschiefe Verteilung aufweist. Zugleich wird ersichtlich, dass die meisten Posts nur wenige Kommentare erhalten. Andererseits scheinen einige Posts sehr erfolgreich zu sein.
faehnrich19 |>
ggplot(aes(x = comments_count)) +
geom_histogram()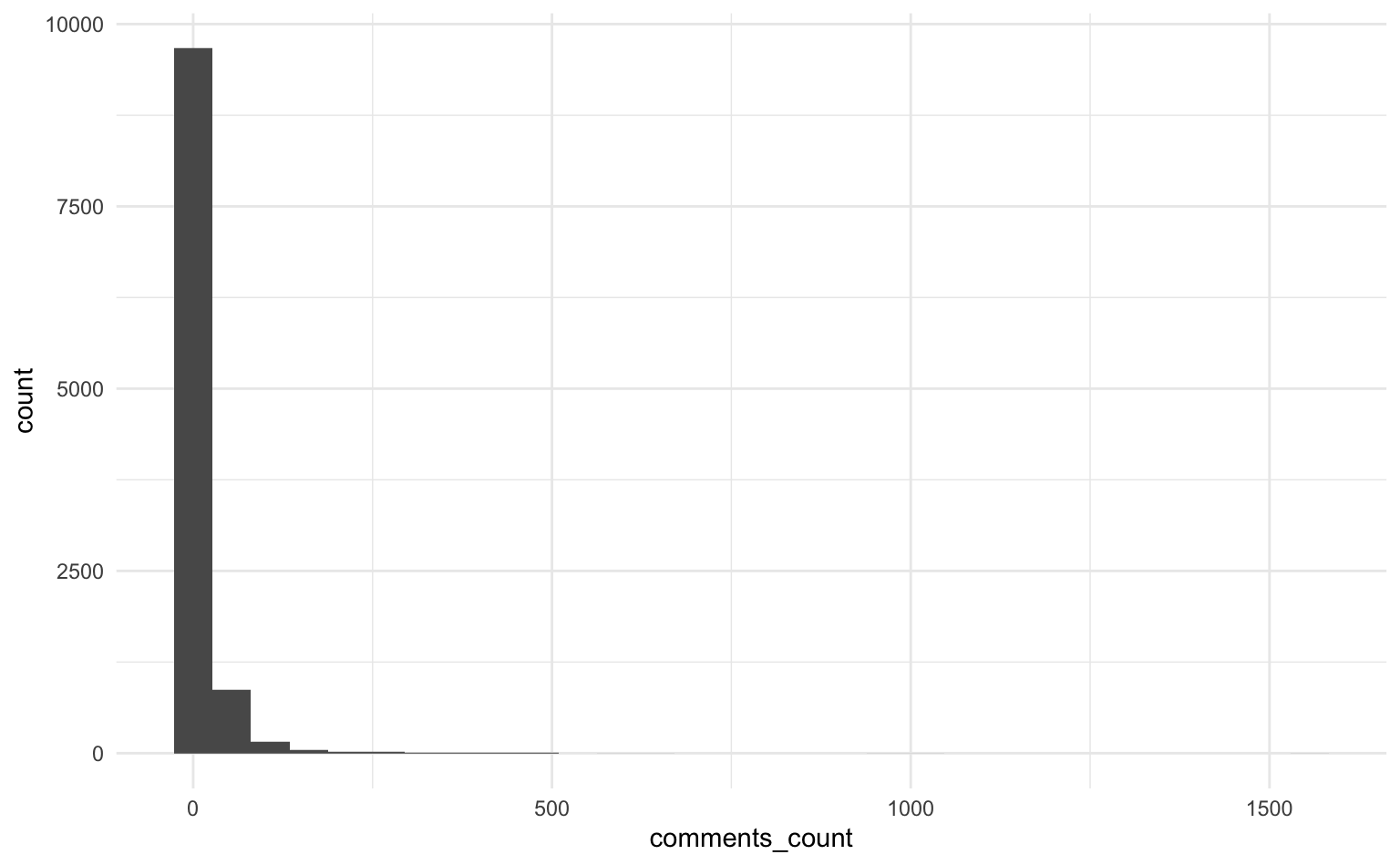
9.3 Nullmodell und ICC
Wie für andere Analyseverfahren können wir auch für Multilevel-Modelle ein Nullmodel berechnen. Dazu ist lediglich eine kleine Änderung in der Formel nötig. Zusätzlich zu der 1 für den Intercept brauchen wir einen Term für die Varying Intercepts, welche die gruppenspezifischen Abweichungen vom Gesamtmittelwert darstellen. Da wir für jede Gruppe, d.h. für jede Universität, einen eigenen Intercept berechnen wollen, müssen wir noch (1 | uni) hinzufügen.
m0 <- lmer(comments_count ~ 1 + (1 | uni), data = faehnrich19)
report_table(m0)Parameter | Coefficient | 95% CI | t(10804) | p | Effects | Group | Std. Coef. | Std. Coef. 95% CI | Fit
-----------------------------------------------------------------------------------------------------------------------------------
(Intercept) | 14.34 | [9.23, 19.44] | 5.50 | < .001 | fixed | | 0.06 | [-0.08, 0.20] |
| 16.71 | | | | random | uni | | |
| 33.32 | | | | random | Residual | | |
| | | | | | | | |
AIC | | | | | | | | | 1.07e+05
AICc | | | | | | | | | 1.07e+05
BIC | | | | | | | | | 1.07e+05
R2 (conditional) | | | | | | | | | 0.20
R2 (marginal) | | | | | | | | | 0.00
Sigma | | | | | | | | | 33.32Das Nullmodel gibt Auskunft darüber, wie sich die Varianz auf die verschiedenen Ebenen verteilt. Diese Varianzen können wir nutzen, um den Intraklassenkorrelationskoeffizient (ICC) zu berechnen, der einen Hinweis darauf gibt, ob ein Multilevel-Modell überhaupt nötig ist.
9.3.1 ICC
Die Informationen für die Berechnung des ICC lassen sich aus der Spalte coefficient entnehmen. Darin enthalten sind die Werte für die Varianz auf beiden Ebenen in Form der Standardabweichungen (= Quadratwurzel der Varianz). Die benötigten Werte werden hier als uni (Level-2) und Residual (Level-1) bezeichnet.
16.71^2 / (16.71^2 + 33.32^2)[1] 0.2009607Etwa 20% der Varianz werden durch die Gruppen erklärt, weshalb es in unserem Fall sinnvoll ist, auf ein Multilevel-Modell zurückzugreifen. Das Paket perfmormance besitzt auch eine dedizierte Funktion icc(), welche ebenfalls den Intraklassenkorrelationskoeffizient berechnet.
performance::icc(m0)# Intraclass Correlation Coefficient
Adjusted ICC: 0.201
Unadjusted ICC: 0.201Interpretation: Etwa 20% der Varianz in der Kommentaranzahl lässt sich ausschließlich durch Unterschiede zwischen den Universitäts-Seiten auf Facebook erklären.
9.3.2 Vorausgesagte Mittelwerte (inkl. Varying Intercepts )
Wir können uns auch die vorhergesagte Anzahl an Kommentaren für die Facebook-Accounts der verschiedenen Universitäten ausgeben lassen. Dazu berechnen wir wieder Average Marginal Effects mit der Funktion avg_predictions.
preds_uni <- marginaleffects::avg_predictions(m0, variables = "uni") |>
as_tibble()
preds_uni# A tibble: 42 × 8
uni estimate std.error statistic p.value s.value conf.low conf.high
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 Columbia U 2.33 2.61 0.894 3.71e- 1 1.43 -2.78 7.44
2 Cornell U 9.40 2.61 3.61 3.08e- 4 11.7 4.29 14.5
3 Duke U 8.69 2.61 3.34 8.52e- 4 10.2 3.58 13.8
4 Harvard U 66.4 2.61 25.5 3.48e-143 473. 61.3 71.5
5 Imperial Co… 3.40 2.61 1.30 1.92e- 1 2.38 -1.71 8.50
# ℹ 37 more rowsWie wir sehen, gibt deutliche Unterschiede zwischen den einzelnen Universitäten. Während bei einigen Facebook-Seiten nur einige wenige Kommentare unter einem Post zu erwarten sind, gibt es einzelne Universitäten, die im Durchschnitt mit 60 oder mehr Kommentaren rechnen können.
9.4 Modell mit Varying Intercepts
9.4.1 Lineares Modell mit Varying Intercepts
Nun fügen wir dem Nullmodell noch die dichotome Variable topic_reseach hinzu, welche auf Level 1 angesiedelt ist, also der Post-Ebene. Der Prädiktor gibt an, ob sich der Facebook-Post mit Forschungsthemen befasst oder nicht.
m1_research <- lmer(comments_count ~ 1 + topic_research + (1 | uni), data = faehnrich19)
report::report_table(m1_research)Parameter | Coefficient | 95% CI | t(10387) | p | Effects | Group | Std. Coef. | Std. Coef. 95% CI | Fit
------------------------------------------------------------------------------------------------------------------------------------
(Intercept) | 15.57 | [10.48, 20.67] | 5.99 | < .001 | fixed | | 0.06 | [-0.08, 0.20] |
topic research | -4.06 | [-5.53, -2.59] | -5.42 | < .001 | fixed | | -0.05 | [-0.07, -0.03] |
| 16.60 | | | | random | uni | | |
| 33.41 | | | | random | Residual | | |
| | | | | | | | |
AIC | | | | | | | | | 1.03e+05
AICc | | | | | | | | | 1.03e+05
BIC | | | | | | | | | 1.03e+05
R2 (conditional) | | | | | | | | | 0.20
R2 (marginal) | | | | | | | | | 2.38e-03
Sigma | | | | | | | | | 33.41Da es sich um ein lineares Modell handelt, kann der Koeffizient direkt interpretiert werden. Entsprechend können wir folgenden Befund festhalten: Posts, die Forschungsthemen behandeln, erhalten durchschnittlich 4 Kommentare weniger als andere Posts. Der Effekt ist statistisch signifikant (p<.001).
9.4.2 Modellvorhersagen
Auch für dieses Modell können wir Average Marginal Effects berechnen.
preds_uni <- avg_predictions(m1_research, variables = c("topic_research", "uni")) |>
as_tibble()
preds_uni# A tibble: 84 × 9
topic_research uni estimate std.error statistic p.value s.value conf.low
<int> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 0 Columb… 3.05 2.60 1.17 2.41e- 1 2.05 -2.05
2 0 Cornel… 10.6 2.60 4.06 4.90e- 5 14.3 5.46
3 0 Duke U 9.29 2.60 3.57 3.51e- 4 11.5 4.20
4 0 Harvar… 67.1 2.60 25.8 4.20e-147 486. 62.0
5 0 Imperi… 5.26 2.60 2.02 4.29e- 2 4.54 0.167
# ℹ 79 more rows
# ℹ 1 more variable: conf.high <dbl>9.4.3 Visualisierung der Vorhersagen
Die AME lassen sich dann auch wieder grafisch darstellen.
preds_uni |>
ggplot(aes(x = factor(topic_research), y = estimate, color = uni, group = uni)) +
geom_line(show.legend = FALSE) +
geom_point(show.legend = FALSE) +
labs(x = "Topic Research", y = "Predicted comments")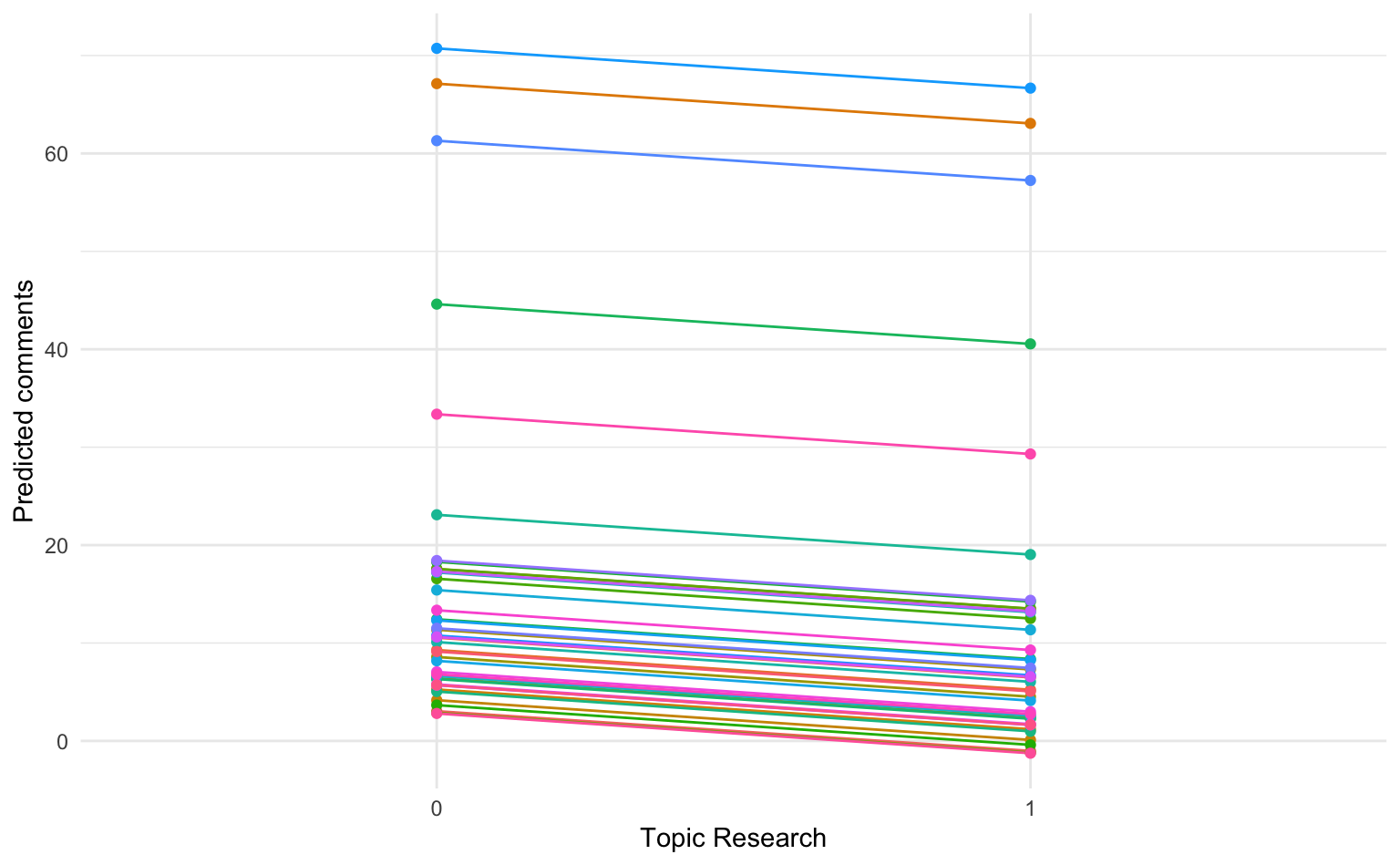
Der negative Effekt von Forschungsthemen in einem Facebook-Post ist im vorliegenden Modell bei allen Universitäten gleich. Die Universitäten unterscheiden sich hier nur durch die Varying Intercepts. Wir sehen auch, dass das Modell für einige Universitäten eine negative Anzahl an Kommentaren vorhersagt, das Modell also nicht sehr gut zu den Daten passt.
9.5 Modell mit Varying Intercepts und Slopes
9.5.1 Varying slopes für Thema Forschung
Multilevel-Modelle können neben Varying Intercepts auch Varying Slopes enthalten. Kurz gesagt bilden Varying Slopes unterschiedliche Effekte einer Variable in den verschiedenen Gruppen ab. In der nachfolgenden Analyse nehmen wir an, dasss Facebook-Posts mit Bezug zur Forschung nicht bei allen Universitäten den gleichen (negativen) Effekt haben. Die Varying Slopes fügen wir hinzu, indem wir die Variable topic_research in die Klammer (1 | uni), welche die Varying Intercepts kennzeichnet, aufnehmen.
m2_research_vs <- lmer(comments_count ~ 1 + topic_research + (1 + topic_research | uni), data = faehnrich19)
report::report_table(m2_research_vs)Parameter | Coefficient | 95% CI | t(10385) | p | Effects | Group | Std. Coef. | Std. Coef. 95% CI | Fit
------------------------------------------------------------------------------------------------------------------------------------
(Intercept) | 15.74 | [10.12, 21.36] | 5.49 | < .001 | fixed | | 0.06 | [-0.08, 0.20] |
topic research | -4.96 | [-7.35, -2.57] | -4.07 | < .001 | fixed | | -0.06 | [-0.09, -0.03] |
| 18.36 | | | | random | uni | | |
| 6.24 | | | | random | uni | | |
| -1.00 | | | | random | uni | | |
| 33.32 | | | | random | Residual | | |
| | | | | | | | |
AIC | | | | | | | | | 1.03e+05
AICc | | | | | | | | | 1.03e+05
BIC | | | | | | | | | 1.03e+05
R2 (conditional) | | | | | | | | | 0.21
R2 (marginal) | | | | | | | | | 3.54e-03
Sigma | | | | | | | | | 33.32summary(m2_research_vs)Linear mixed model fit by REML ['lmerMod']
Formula: comments_count ~ 1 + topic_research + (1 + topic_research | uni)
Data: faehnrich19
REML criterion at convergence: 102515.8
Scaled residuals:
Min 1Q Median 3Q Max
-2.259 -0.215 -0.077 0.010 44.436
Random effects:
Groups Name Variance Std.Dev. Corr
uni (Intercept) 337.06 18.36
topic_research 38.94 6.24 -1.00
Residual 1110.39 33.32
Number of obs: 10391, groups: uni, 42
Fixed effects:
Estimate Std. Error t value
(Intercept) 15.740 2.869 5.486
topic_research -4.959 1.220 -4.065
Correlation of Fixed Effects:
(Intr)
topic_rsrch -0.831
optimizer (nloptwrap) convergence code: 0 (OK)
boundary (singular) fit: see help('isSingular')Erneut sehen wir, dass Forschungsthemen mit einer niedrigeren Anzahl Kommentaren zusammenhängen. Interessant ist, dass der negative Zusammenhang laut Modell stark von den Universitäten abhängt, wie wir aus der berechneten Standardabweichung von 6.24 für die Varying Slopes ablesen können (zur Erinnerung: ca. 2/3 aller Koeffizienten liegen +- 1 SD um den mittleren Effekt).
9.5.2 Modellvergleich Fixed vs. Varying Slopes
Um unsere beiden Modelle zu vergleichen, können wir die anova()-Funktion nutzen, um einen Likelihood-Ratio-Test durchzuführen.
anova(m1_research, m2_research_vs)Data: faehnrich19
Models:
m1_research: comments_count ~ 1 + topic_research + (1 | uni)
m2_research_vs: comments_count ~ 1 + topic_research + (1 + topic_research | uni)
npar AIC BIC logLik deviance Chisq Df Pr(>Chisq)
m1_research 4 102583 102612 -51287 102575
m2_research_vs 6 102533 102576 -51260 102521 53.934 2 1.942e-12 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Der Test zeigt an, dass das Varying Slopes und Intercept Modell signifikant besser ist als das Varying Intercept Modell (p<.001), d.h. es gibt signifikante Effektheterogenität bezüglich des Prädiktors Forschungsthema.
9.5.3 Varying slopes pro Uni
AMEs lassen sich ebenfalls für die Varying Slopes berechnen. Dafür gibt es eine spezielle Funktion avg_slopes().
marginaleffects::avg_slopes(m2_research_vs, by = "uni") |>
as_tibble()# A tibble: 42 × 13
term contrast uni estimate std.error statistic p.value s.value conf.low
<chr> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 topic_r… mean(1)… Colu… -0.433 1.22 -0.355 7.23e- 1 0.469 -2.82
2 topic_r… mean(1)… Corn… -3.15 1.22 -2.58 9.81e- 3 6.67 -5.54
3 topic_r… mean(1)… Duke… -2.72 1.22 -2.23 2.57e- 2 5.28 -5.11
4 topic_r… mean(1)… Harv… -24.6 1.22 -20.2 2.31e-90 298. -27.0
5 topic_r… mean(1)… Impe… -0.914 1.22 -0.749 4.54e- 1 1.14 -3.30
# ℹ 37 more rows
# ℹ 4 more variables: conf.high <dbl>, predicted_lo <dbl>, predicted_hi <dbl>,
# predicted <dbl>9.5.4 Modellvorhersagen
Wir können wieder avg_predictions() nutzen, um Vorhersagen für die Anzahl der Kommentare unter Posts mit und ohne Wissenschaftsbezug für die einzelnen Universitäten zu erhalten.
preds_uni_vs <- avg_predictions(m2_research_vs, variables = c("topic_research", "uni")) |>
as_tibble()
preds_uni_vs# A tibble: 84 × 9
topic_research uni estimate std.error statistic p.value s.value conf.low
<int> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 0 Columb… 2.42 2.87 0.845 3.98e- 1 1.33 -3.20
2 0 Cornel… 10.4 2.87 3.63 2.82e- 4 11.8 4.80
3 0 Duke U 9.16 2.87 3.19 1.42e- 3 9.46 3.53
4 0 Harvar… 73.5 2.87 25.6 9.35e-145 478. 67.9
5 0 Imperi… 3.84 2.87 1.34 1.81e- 1 2.47 -1.79
# ℹ 79 more rows
# ℹ 1 more variable: conf.high <dbl>9.5.5 Visualisierung der Vorhersagen
preds_uni_vs |>
ggplot(aes(x = factor(topic_research), y = estimate, color = uni, group = uni)) +
geom_line(show.legend = FALSE) +
geom_point(show.legend = FALSE) +
labs(x = "Topic Research", y = "Predicted comments")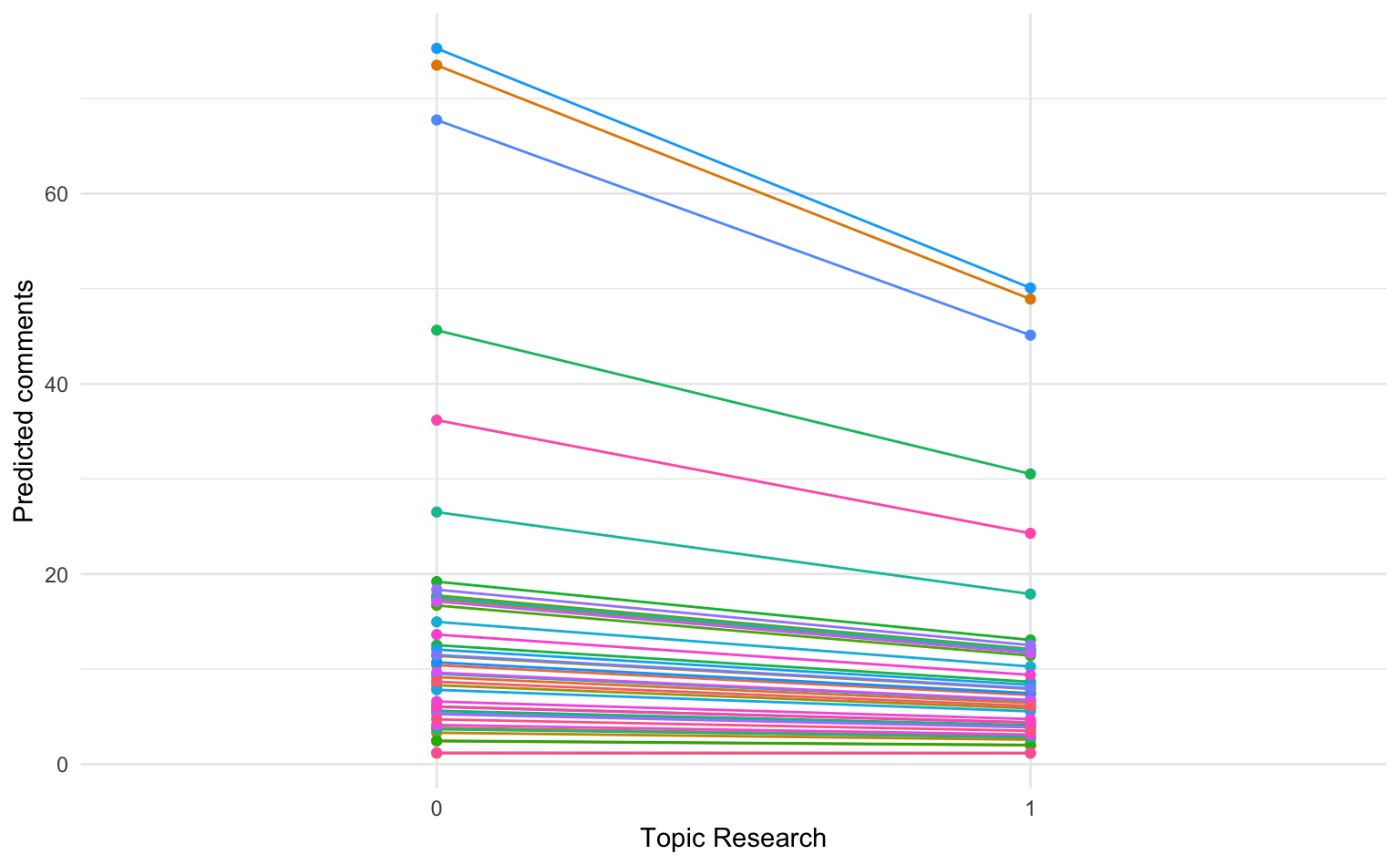
Die Visualisierung zeigt deutlich, dass Posts mit Bezug zu Forschungsthemen bei einigen Universitäten nur geringfügig die vorhergesagte Anzahl an Kommentaren (= flachere Gerade) beeinflusst, während bei anderen deutlich stärkere negative Effekte auftreten.
9.6 Modell mit Level-2-Prädiktor
Bislang haben wir mit topic_research lediglich einen Level-1-Prädiktor für unsere Analyse verwendet. Es ist aber ebenso möglich, einen Level-2-Prädiktor in das Modell aufzunehmen, um die Unterschiede zwischen den Gruppen zu erklären. Die Anzahl der Kommentare sollte bei allen Posts davon abhängen, wieviele Fans die Facebook-Seite der Universität hat, allein schon weil mehr NutzerInnen diese Posts zu sehen bekommen. Deshalb fügen wir die Variable uni_fans in die Formel ein.
m3_research_fans <- lmer(comments_count ~ 1 + topic_research + uni_fans + (1 + topic_research | uni), data = faehnrich19)
report::report_table(m3_research_fans)Parameter | Coefficient | 95% CI | t(10384) | p | Effects | Group | Std. Coef. | Std. Coef. 95% CI | Fit
------------------------------------------------------------------------------------------------------------------------------------
(Intercept) | 10.88 | [ 6.56, 15.19] | 4.94 | < .001 | fixed | | 0.05 | [-0.04, 0.15] |
topic research | -5.69 | [-8.35, -3.04] | -4.21 | < .001 | fixed | | -0.07 | [-0.10, -0.04] |
uni fans | 0.01 | [ 0.01, 0.01] | 8.18 | < .001 | fixed | | 0.21 | [ 0.16, 0.26] |
| 13.41 | | | | random | uni | | |
| 7.26 | | | | random | uni | | |
| -0.99 | | | | random | uni | | |
| 33.32 | | | | random | Residual | | |
| | | | | | | | |
AIC | | | | | | | | | 1.03e+05
AICc | | | | | | | | | 1.03e+05
BIC | | | | | | | | | 1.03e+05
R2 (conditional) | | | | | | | | | 0.16
R2 (marginal) | | | | | | | | | 0.05
Sigma | | | | | | | | | 33.32Wie wir sehen, hängt die Anzahl der Fans positiv mit der Anzahl an Kommentaren zusammen. Der Effekt ist statistisch signifikant (p<.001). Allerdings zeigt sich auch, dass der Koeffizient topic_research nun einen noch stärkeren negativen Effekt zeigt Keine guten Aussichten für die Wissenschaftler, die sich mit ihrer Forschung auf sozialen Medien präsentieren wollen…