2 Lineare Regression
Beispielanalyse
Wie hängen Alter und Musiknutzung zusammen?
2.1 Pakete und Daten laden
Zunächst laden wir die üblichen R-Pakete sowie die Daten von Johannes et al. (2022).
library(report)
library(tidyverse)
theme_set(theme_minimal())johannes22 <- haven::read_sav("data/Johannes_2022.sav") |>
haven::zap_labels()
johannes22# A tibble: 2,159 × 11
id gender age music_time films_time tv_time games_time books_time
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1112 2 22 4 0 0 0 0
2 2048 1 43 2.5 2 0 0 0
3 2357 1 38 0.167 0.333 2 0 0
4 3531 2 30 2 14 5 0 2
5 3642 2 29 0.75 0.5 1.5 1 0.5
# ℹ 2,154 more rows
# ℹ 3 more variables: magazines_time <dbl>, audiobooks_time <dbl>,
# total_time <dbl>Die für uns relevanten Variablen sind Alter (age) und die Zeit, die die Befragten täglich Musik hören (music_time).
2.2 Deskriptivstatistik
Wir betrachten zunächst die Outcome-Variable music_time deskriptiv und grafisch.
johannes22 |>
select(music_time) |>
report::report_table()Variable | n_Obs | Mean | SD | Median | MAD | Min | Max | Skewness | Kurtosis | percentage_Missing
----------------------------------------------------------------------------------------------------------
music_time | 2159 | 2.14 | 2.75 | | 1.98 | 0.00 | 22.22 | 2.39 | 8.67 | 2.59johannes22 |>
ggplot(aes(x = music_time)) +
geom_histogram()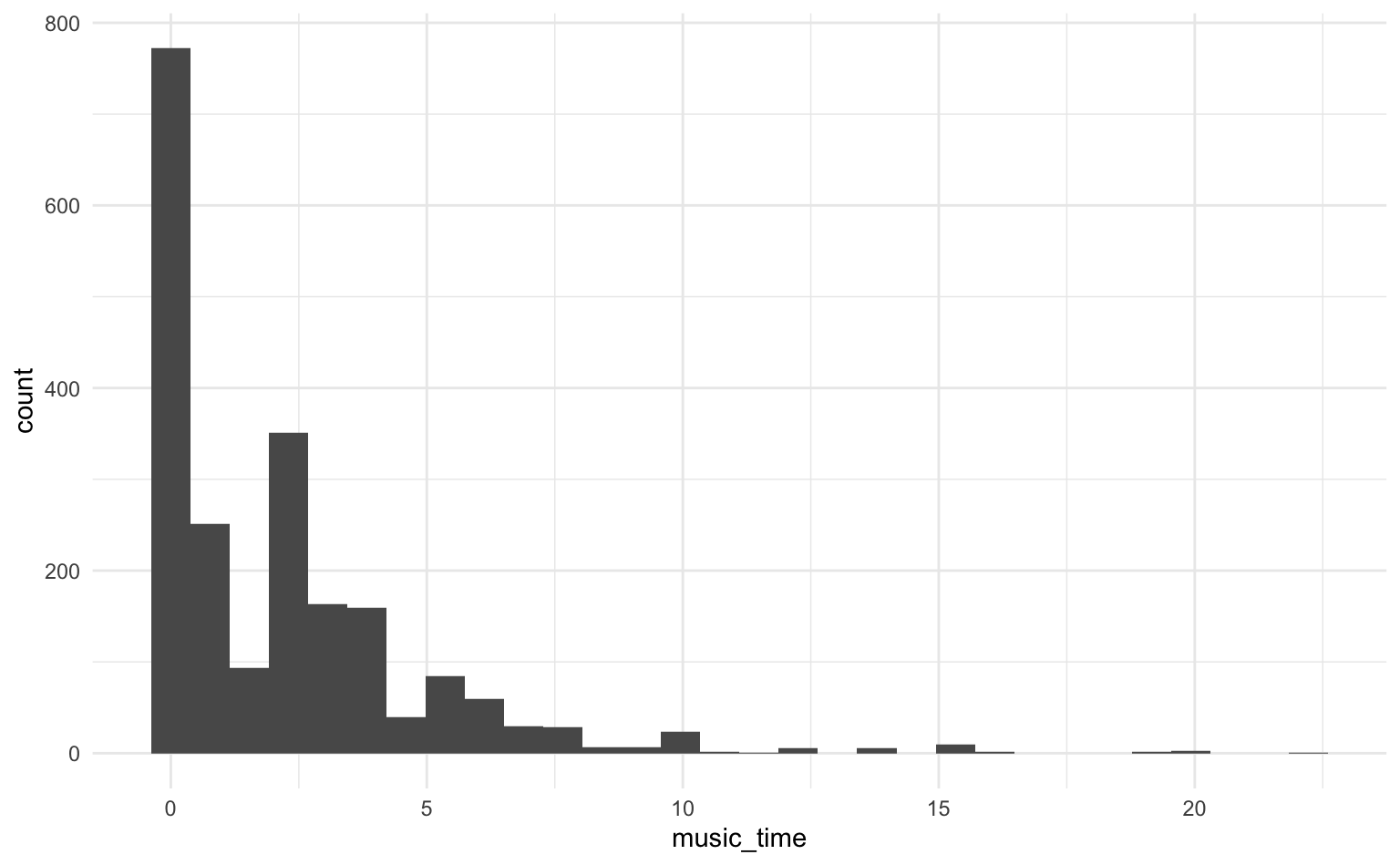
2.3 Scatterplot mit Regressionsgerade
Bei einer bivariaten Analyse lohnt es sich immer, zunächste ein Punktdiagramm der beiden Variablen zu erstellen. Zusätzlich wird mit geom_smooth() die Regressionsgerade eingezeichnet.
johannes22 |>
ggplot(aes(x = age, y = music_time)) +
geom_point() +
geom_smooth(method = "lm")
Wir erkennen einen schwachen negativen Zusammenhang, den wir nachfolgend statistisch testen.
2.4 Bivariate Regression
m1_age <- lm(music_time ~ age, data = johannes22)
report::report_table(m1_age)Parameter | Coefficient | 95% CI | t(2101) | p | Std. Coef. | Std. Coef. 95% CI | Fit
---------------------------------------------------------------------------------------------------------
(Intercept) | 4.04 | [ 3.65, 4.42] | 20.53 | < .001 | 3.72e-17 | [-0.04, 0.04] |
age | -0.04 | [-0.05, -0.03] | -10.14 | < .001 | -0.22 | [-0.26, -0.17] |
| | | | | | |
AIC | | | | | | | 10125.18
AICc | | | | | | | 10125.19
BIC | | | | | | | 10142.13
R2 | | | | | | | 0.05
R2 (adj.) | | | | | | | 0.05
Sigma | | | | | | | 2.68Ergebnis: Eine Altersdifferenz von einem Jahr geht mit 0,04 Stunden weniger Musikhören einher (B = -0.04, 95% CI [-0.05, -0.03], t(2101) = -10.14, p < .001). Der Effekt ist statistisch signifikant, aber schwach, wie wir am standardisierten Koeffizienten bzw. am \(R^2\) erkennen können.
Der Intercept von 4,04h am Tag entspricht dem vorhergesagten Wert, wenn Alter = 0, d.h. für Neugeborene, was keine sinnvolle Vergleichsgröße ist, u.a. weil keine Neugeborenen in der Stichprobe waren.
2.5 Variablen transformieren
Um die Auswirkungen verschiedener Datentransformationen zu prüfen, erstellen wir einige neues Variablen mit dem mutate()-Befehl (siehe Datentransformationen). Wir erstellen eine Variable age18, bei der die Null dem Alter 18 entspricht sowie eine mittelwertzentrierte Variable age_centered, bei dem die 0 dem Stichprobenmittelwert im Alter entspricht. Wir erstellen z-standardisierte Varianten von Alter und Musikhören sowie ein transformiertes Outcome (Musikhören in Minuten am Tag).
johannes22 <- johannes22 |>
mutate(
age18 = age - 18,
age_centered = age - mean(age, na.rm = TRUE),
age_zstd = scale(age),
music_time_zstd = scale(music_time),
music_time_m = music_time * 60
)2.6 Zentrierter Prädiktor
m1_age18 <- lm(music_time ~ age18, data = johannes22)
report::report_table(m1_age18)Parameter | Coefficient | 95% CI | t(2101) | p | Std. Coef. | Std. Coef. 95% CI | Fit
---------------------------------------------------------------------------------------------------------
(Intercept) | 3.31 | [ 3.06, 3.57] | 25.49 | < .001 | -4.31e-17 | [-0.04, 0.04] |
age18 | -0.04 | [-0.05, -0.03] | -10.14 | < .001 | -0.22 | [-0.26, -0.17] |
| | | | | | |
AIC | | | | | | | 10125.18
AICc | | | | | | | 10125.19
BIC | | | | | | | 10142.13
R2 | | | | | | | 0.05
R2 (adj.) | | | | | | | 0.05
Sigma | | | | | | | 2.68Verwenden wir age18 als unabhängige Variable, ändert sich nur der Intercept. Dieser entspricht jetzt dem vorhergesagten Wert von Musik hören bei 18-Jährigen. Alle anderen Modellkoeffizienten ändern sich nicht.
2.7 Mittelwertzentrierter Prädiktor
m1_age_c <- lm(music_time ~ age_centered, data = johannes22)
report::report_table(m1_age_c)Parameter | Coefficient | 95% CI | t(2101) | p | Std. Coef. | Std. Coef. 95% CI | Fit
----------------------------------------------------------------------------------------------------------
(Intercept) | 2.14 | [ 2.03, 2.25] | 36.56 | < .001 | -4.31e-17 | [-0.04, 0.04] |
age centered | -0.04 | [-0.05, -0.03] | -10.14 | < .001 | -0.22 | [-0.26, -0.17] |
| | | | | | |
AIC | | | | | | | 10125.18
AICc | | | | | | | 10125.19
BIC | | | | | | | 10142.13
R2 | | | | | | | 0.05
R2 (adj.) | | | | | | | 0.05
Sigma | | | | | | | 2.68In diesem Modell entspricht der Intercept dem vorhergesagten Wert für eine durchschnittlich alte Befragte. Alle anderen Modellkoeffizienten ändern sich nicht.
2.8 Transformiertes Outcome
m1_minutes <- lm(music_time_m ~ age_centered, data = johannes22)
report::report_table(m1_minutes)Parameter | Coefficient | 95% CI | t(2101) | p | Std. Coef. | Std. Coef. 95% CI | Fit
------------------------------------------------------------------------------------------------------------
(Intercept) | 128.40 | [121.51, 135.28] | 36.56 | < .001 | 1.14e-16 | [-0.04, 0.04] |
age centered | -2.43 | [ -2.90, -1.96] | -10.14 | < .001 | -0.22 | [-0.26, -0.17] |
| | | | | | |
AIC | | | | | | | 27345.99
AICc | | | | | | | 27346.01
BIC | | | | | | | 27362.95
R2 | | | | | | | 0.05
R2 (adj.) | | | | | | | 0.05
Sigma | | | | | | | 161.06Verwenden wir ein transformiertes Outcome, ändert sich die Interpretation von Intercept und Regressionskoeffizienten. Diese sind jetzt in Minuten/Tag skaliert, d.h. ein Jahr Altersunterschied entspricht 2,43 Minuten weniger Musikhören am Tag. Die standardisierten Koeffizienten sind davon nicht betroffen, ebenso wenig die anderen Modellkoeffizienten, etwa die Gütemaße.
2.9 Standardisierte Variablen
In diesem Modell verwenden wir die z-standardisierte unabhängige und abhängige Variablen. Dementsprechend sollten im Modell-Output unstandardisierte und standardisierte Regressionskoeffizienten identisch sein.
m1_zstd <- lm(music_time_zstd ~ age_zstd, data = johannes22)
report::report_table(m1_zstd)Parameter | Coefficient | 95% CI | t(2101) | p | Std. Coef. | Std. Coef. 95% CI | Fit
--------------------------------------------------------------------------------------------------------
(Intercept) | 1.70e-03 | [-0.04, 0.04] | 0.08 | 0.936 | 2.07e-16 | [-0.04, 0.04] |
age zstd | -0.22 | [-0.26, -0.17] | -10.14 | < .001 | -0.22 | [-0.26, -0.17] |
| | | | | | |
AIC | | | | | | | 5872.64
AICc | | | | | | | 5872.65
BIC | | | | | | | 5889.59
R2 | | | | | | | 0.05
R2 (adj.) | | | | | | | 0.05
Sigma | | | | | | | 0.98Der Intercept-Term muss durch die Standardisierung (bis auf einen Rundungsfehler) 0 sein, und der Alterseffekt ist wie erwartet identisch.