library(marginaleffects)
library(report)
library(tidyverse)
theme_set(theme_minimal())7 Moderationsanalyse
Beispielanalyse
Wie wirkt der Dialekt von Politikern auf deren Bewertung?
7.1 Pakete und Daten laden
Wir beginnen mit den üblichen R-Paketen, die wir für die Analyse verwenden wollen. Hinzu kommt das Paket marginaleffects, welches Modellvorhersagen für die Interpretation der Koeffizienten enthält.
Weiter laden wir den Datensatz von Vögele und Bachl (2017). Zudem erstellen wir eine neue Variable geschlecht_w, die den Wert 1 annimmt, wenn es sich um eine Frau handelt.
vb17 <- haven::read_sav("data/Voegele_Bachl_2017.sav") |>
mutate(geschlecht_w = ifelse(Geschlecht == 1, 1, 0)) |>
haven::zap_labels()
vb17# A tibble: 363 × 28
gesamt lire Geschlecht alter schwab atol klischee klang verst polint gender
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 4 1 2 29 0 2.4 3.5 4.67 5 3 0
2 4 3 2 25 0 3 2.88 4 5 3 0
3 4 3 2 51 0 3.6 3.5 4 3.75 2 0
4 4 3 1 65 0 2.6 2.62 3 3.75 3 0
5 5 5 1 67 0 3 3.12 4.67 4.5 5 0
# ℹ 358 more rows
# ℹ 17 more variables: atol_centered <dbl>, atol_1 <dbl>, atol_2 <dbl>,
# atol_3 <dbl>, atol_4 <dbl>, atol_5 <dbl>, Filter_Wahlberechtigung <dbl>,
# `filter_$` <dbl>, kom <dbl>, leadership <dbl>, integrity <dbl>,
# sympathy <dbl>, mod <dbl>, mean_atol <dbl>, schwab_geschlecht <dbl>,
# schwab_atol_centered <dbl>, geschlecht_w <dbl>7.2 Deskriptivstatistik
Zunächst betrachten wir die Outcome-Variable gesamt, welche die Gesamtbewertung des Politikers beschreibt.
vb17 |>
select(gesamt) |>
report::report_table()Variable | n_Obs | Mean | SD | Median | MAD | Min | Max | Skewness | Kurtosis | percentage_Missing
-------------------------------------------------------------------------------------------------------
gesamt | 363 | 3.70 | 0.88 | 4.00 | 0.00 | 1.00 | 5.00 | -0.69 | 0.45 | 0.00Höhere Werte bedeuten, dass die Befragten einen besseren Eindruck des Politikers hatten. Die Daten zeigen, dass im Durchschnitt eher ein guter Eindruck überwogen hat (M = 3.70; SD = 0.88).
Wir können mittels eines Histograms darstellen, welche Bewertung wie häufig vergeben wurde.
vb17 |>
ggplot(aes(x = gesamt)) +
geom_histogram()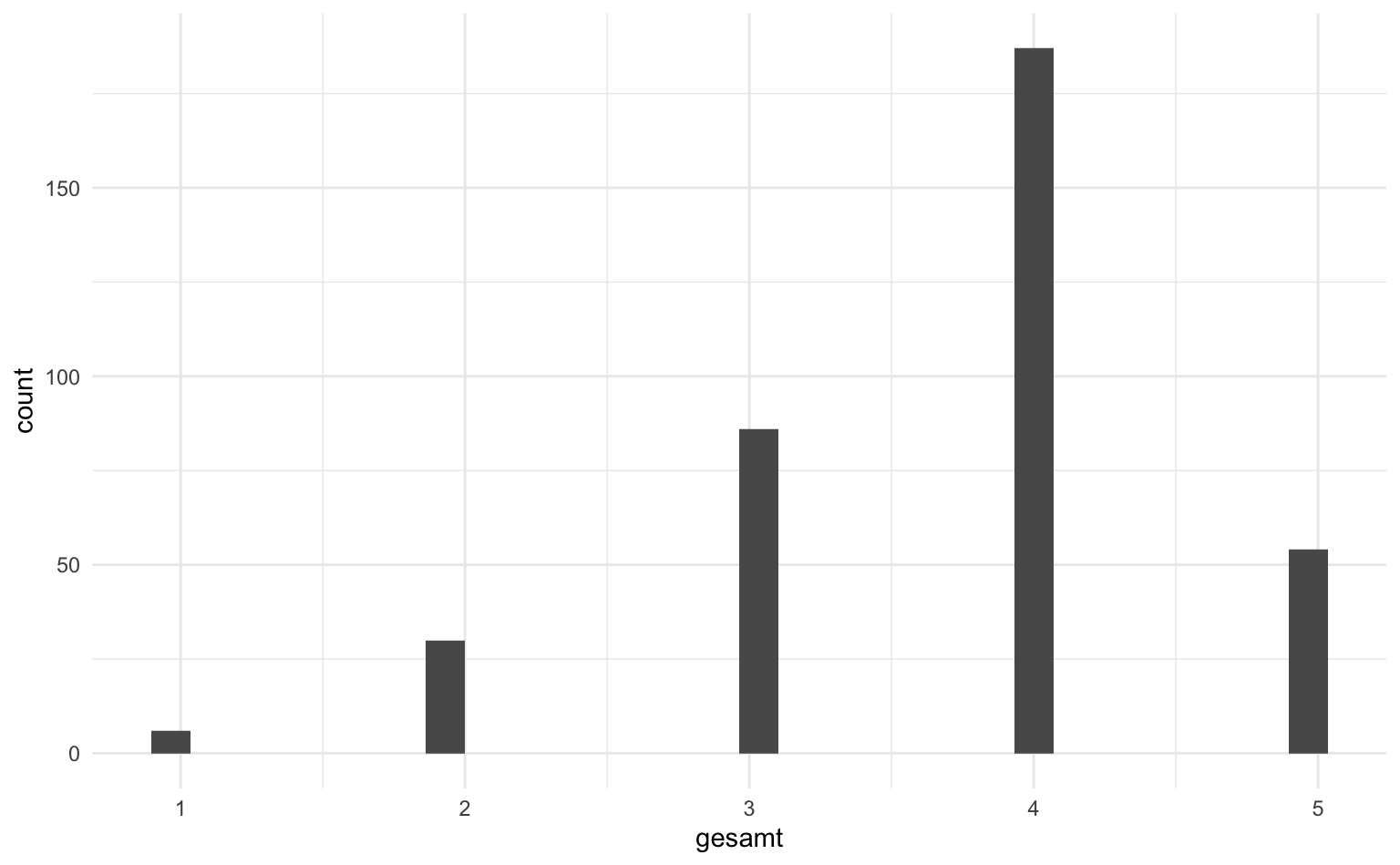
Es zeigt sich, dass die meisten Befragten eine eher positive Bewertung (4) vergeben haben.
7.3 Interaktion mit kategorieller Moderatorvariable
7.3.1 Unkonditionales Modell
Das erste Regressionsmodell enthält keinen Interaktionseffekt, sondern lediglich das Geschlecht und eine Indikatorvariable, welche angibt, ob der Politiker einen schwäbischen Dialekt spricht (1) oder nicht (0). Es handelt sich also hierbei um eine simple multiple Regression, die wir bereits kennengelernt haben.
lm(gesamt ~ schwab + geschlecht_w, data = vb17) |>
report::report_table()Parameter | Coefficient | 95% CI | t(360) | p | Std. Coef. | Std. Coef. 95% CI | Fit
-------------------------------------------------------------------------------------------------------
(Intercept) | 3.63 | [ 3.46, 3.79] | 43.52 | < .001 | -8.66e-16 | [-0.10, 0.10] |
schwab | -0.21 | [-0.39, -0.03] | -2.31 | 0.021 | -0.12 | [-0.22, -0.02] |
geschlecht w | 0.34 | [ 0.16, 0.52] | 3.75 | < .001 | 0.19 | [ 0.09, 0.29] |
| | | | | | |
AIC | | | | | | | 925.97
AICc | | | | | | | 926.08
BIC | | | | | | | 941.54
R2 | | | | | | | 0.05
R2 (adj.) | | | | | | | 0.05
Sigma | | | | | | | 0.86Beide Variablen sagen signifikant die Gesamtbewertung des Politikers voraus. Männliche und weibliche Befragte unterscheiden sich um einen drittel Skalenpunkt, sowie Dialektspecher um einen fünftel Skalenpunkt. Der Intercept lässt sich hier direkt interpretieren. Er stellt die durchschnittliche Bewertung des nicht schwäbisch sprechenden Politikers (schwab = 0) durch einen Mann (geschlecht_w = 0) dar. Die Varianzaufklärung des Modells ist mit 5% eher niedrig.
7.3.2 Geschlecht als Moderator
Nachfolgend nehmen wir an, dass das Geschlecht (= Moderator) einen moderierenden Einfluss auf die Beziehung zwischen Dialektsprechern und der Gesamtbewertung hat. Einen Moderationseffekt (auch Interaktionseffekt) können wir in R spezifizieren, in dem wir die beiden Variablen, die miteinander interagieren, mit einem Doppelpunkt (:) verbinden anstatt eines Pluszeichens (+). In unserem Fall sieht dieser Interaktionsterm dann so aus: schwab:geschlecht_w. Verwenden wir den Doppelpunkt müssen wir den Prädiktor (Dialektsprecher) als auch die Moderationsvariable (Geschlecht) mit in die Formel aufnehmen.
m1_geschlecht <- lm(gesamt ~ schwab + geschlecht_w + schwab:geschlecht_w, data = vb17)
report::report_table(m1_geschlecht)Parameter | Coefficient | 95% CI | t(359) | p | Std. Coef. | Std. Coef. 95% CI | Fit
----------------------------------------------------------------------------------------------------------------
(Intercept) | 3.71 | [ 3.51, 3.90] | 37.37 | < .001 | -1.15e-03 | [-0.10, 0.10] |
schwab | -0.36 | [-0.62, -0.09] | -2.66 | 0.008 | -0.12 | [-0.22, -0.02] |
geschlecht w | 0.19 | [-0.07, 0.46] | 1.42 | 0.158 | 0.19 | [ 0.09, 0.29] |
schwab × geschlecht w | 0.27 | [-0.09, 0.63] | 1.49 | 0.137 | 0.08 | [-0.02, 0.18] |
| | | | | | |
AIC | | | | | | | 925.73
AICc | | | | | | | 925.89
BIC | | | | | | | 945.20
R2 | | | | | | | 0.06
R2 (adj.) | | | | | | | 0.05
Sigma | | | | | | | 0.86Wie sich herausstellt, ist der Interaktionsterm nicht statistisch signifikant, d.h. der Treatment-Effekt variiert nicht signifikant nach Geschlecht der VersuchsteilnehmerInnen. Die konstitutiven Teile des Interaktionseffekts werden Haupteffekte genannt. Hier ist lediglich die Nutzung des schwäbischen Dialekts statistisch signifikant (p = .008). Diese Haupteffekte sind konditional, d.h. abhängig vom Interaktionseffekt, weshalb wir sie hier nicht direkt interpretieren.
7.3.3 Haupteffekte (average marginal effects)
Zur Interpretation der Haupteffekte nutzen wir die Funktion avg_slopes(). Diese Funktion berechnet den Average Marginal Effect (AME). Das bedeutet, dass die Funktion für jeden Fall (= Person) in der Stichprobe den Effekt der Prädiktoren auf die abhängige Variable berechnet. Anschließend wird der Durchschnitt gebildet. Auf diese Weise erhalten wir die Haupteffekte.
marginaleffects::avg_slopes(m1_geschlecht) |>
as_tibble()# A tibble: 2 × 12
term contrast estimate std.error statistic p.value s.value conf.low conf.high
<chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 gesc… mean(1)… 0.341 0.0906 3.76 1.70e-4 12.5 0.163 0.518
2 schw… mean(1)… -0.210 0.0906 -2.31 2.08e-2 5.59 -0.387 -0.0319
# ℹ 3 more variables: predicted_lo <dbl>, predicted_hi <dbl>, predicted <dbl>Diese Koeffizienten entsprechen denen des unkonditionalen Models.
7.3.4 Konditionale Effekte für Dialekt in Abhängigkeit von Geschlecht
Mit dem Funktionsargument by können wir die konditionalen Effekte für Dialekt in Abhängigkeit von Geschlecht berechnen.
marginaleffects::avg_slopes(m1_geschlecht, variable = "schwab", by = "geschlecht_w") |>
as_tibble()# A tibble: 2 × 13
term contrast geschlecht_w estimate std.error statistic p.value s.value
<chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 schwab mean(1) - me… 0 -0.358 0.135 -2.66 0.00778 7.01
2 schwab mean(1) - me… 1 -0.0869 0.123 -0.709 0.478 1.06
# ℹ 5 more variables: conf.low <dbl>, conf.high <dbl>, predicted_lo <dbl>,
# predicted_hi <dbl>, predicted <dbl>Das Ergebnis zeigt uns, dass Männer stark negativ auf dialekt sprechende Politiker reagieren (B = -0.35), während sich bei Frauen nur ein geringer Effekt zeigt (B = -0.086).
7.3.5 Modellvorhersagen (Dialekt und Geschlecht)
Wir können auch die durchschnittlichen vorhergesagten Bewertungen des Politikers für verschiedene Werte der Variablen Dialekt und Geschlecht berechnen. Dazu nutzen wir avg_predictions().
preds_schwab_geschlecht <- marginaleffects::avg_predictions(m1_geschlecht, variables = c("schwab", "geschlecht_w")) |>
as_tibble()
preds_schwab_geschlecht# A tibble: 4 × 9
schwab geschlecht_w estimate std.error statistic p.value s.value conf.low
<int> <int> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 0 0 3.71 0.0992 37.4 1.08e-305 1013. 3.51
2 1 0 3.35 0.0910 36.8 4.47e-296 981. 3.17
3 0 1 3.90 0.0916 42.6 0 Inf 3.72
4 1 1 3.81 0.0815 46.7 0 Inf 3.65
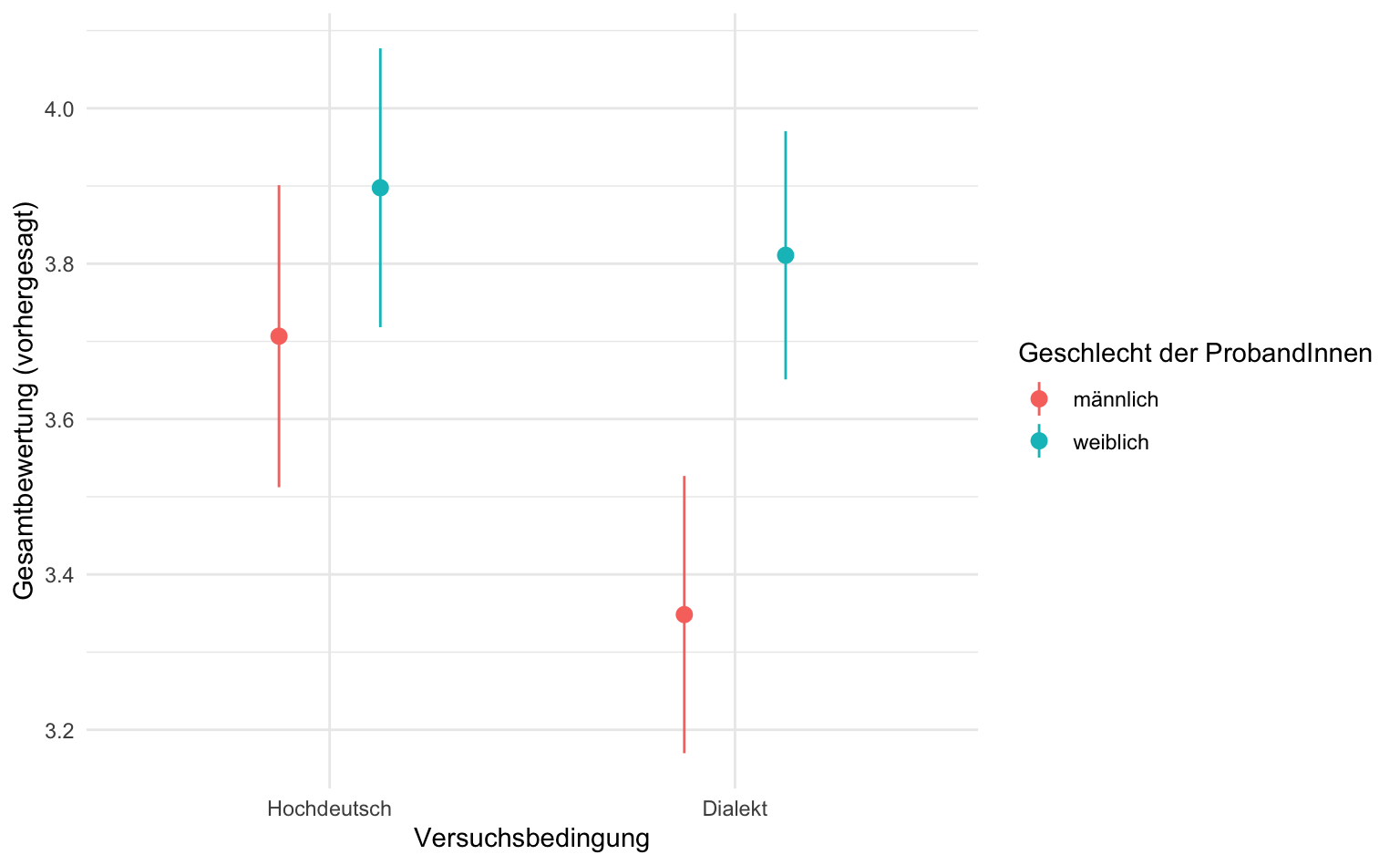
# ℹ 1 more variable: conf.high <dbl>Die vohergesagten Werte bestätigen die Ergebnisse unserer Analyse der Koeffizienten mit avg_slopes. Männer bewerten schwäbisch sprechende Politiker mehr als eine drittel Skalenpunkt schlechter, während sich bei Frauen die vorhergesaten Werte kaum unterscheiden.
7.3.6 Visualisierung der Vorhersagen
Anschaulicher wird es, wenn wir diese Vorhersagen auch grafisch darstellen.
preds_schwab_geschlecht |>
mutate(schwab = factor(schwab), geschlecht_w = factor(geschlecht_w)) |>
ggplot(aes(
x = schwab, y = estimate, group = geschlecht_w,
color = geschlecht_w, ymin = conf.low, ymax = conf.high
)) +
geom_pointrange(position = position_dodge(.5)) +
scale_x_discrete(labels = c("Hochdeutsch", "Dialekt")) +
scale_color_discrete(labels = c("männlich", "weiblich")) +
labs(
y = "Gesamtbewertung (vorhergesagt)",
x = "Versuchsbedingung",
color = "Geschlecht der ProbandInnen"
)
7.4 Interaktion mit metrischer Moderatorvariable
Statt der Notation mit Doppelpunkten (:) können wir auch das Sternchen (*) für den Interaktionsterm nutzen, womit wir uns etwa Schreibarbeit sparen. Verwenden wir das Sternchen werden die konstitutiven Teile des Interaktionsterms automatisch in die Formel hinzugefügt, weshalb wir diese nicht selbst ausschreiben müssen. Nachfolgend wollen wir überprüfen, ob der Effekt des Dialektgebrauchs auf die Politikerbewertung von der Voreinstellung der Befragten gegenüber der schwäbischen Mundart (atol) abhängig ist. Höhere Werte der Variable atol bedeuten eine positivere Voreinstellung.
m2_atol <- lm(gesamt ~ schwab * atol, data = vb17)
report::report_table(m2_atol)Parameter | Coefficient | 95% CI | t(359) | p | Std. Coef. | Std. Coef. 95% CI | Fit
--------------------------------------------------------------------------------------------------------
(Intercept) | 4.19 | [ 3.60, 4.79] | 13.79 | < .001 | 6.91e-03 | [-0.09, 0.11] |
schwab | -1.53 | [-2.32, -0.74] | -3.80 | < .001 | -0.11 | [-0.21, -0.01] |
atol | -0.12 | [-0.29, 0.06] | -1.30 | 0.196 | 0.09 | [-0.01, 0.19] |
schwab × atol | 0.40 | [ 0.17, 0.64] | 3.40 | < .001 | 0.18 | [ 0.07, 0.28] |
| | | | | | |
AIC | | | | | | | 926.81
AICc | | | | | | | 926.98
BIC | | | | | | | 946.29
R2 | | | | | | | 0.05
R2 (adj.) | | | | | | | 0.05
Sigma | | | | | | | 0.86Wie sich herausstellt, ist der Interaktionsterm statistisch signifikant, d.h. der Treatment-Effekt variiert signifikant nach der Voreinstellung der VersuchsteilnehmerInnen zur schwäbischen Mundart. Zudem ist die Nutzung des schwäbischen Dialekts statistisch signifikant (p < .001).
7.4.1 Haupteffekte (average marginal effects)
Wir wiederholen an dieser Stelle das Vorgehen aus dem vorherigen Kapitel und berechnen die Haupteffekte mittels avg_slopes().
marginaleffects::avg_slopes(m2_atol) |>
as_tibble()# A tibble: 2 × 12
term contrast estimate std.error statistic p.value s.value conf.low conf.high
<chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 atol mean(dY… 0.106 0.0587 1.81 0.0703 3.83 -0.00881 0.221
2 schw… mean(1)… -0.201 0.0908 -2.21 0.0271 5.21 -0.379 -0.0228
# ℹ 3 more variables: predicted_lo <dbl>, predicted_hi <dbl>, predicted <dbl>Die Berechnungen zeigen einen positiven Effekt der Voreinstellung und einen negativen des Dialekts, wobei nur der Haupteffekt der Mundart statistisch signifikant ist (p = .027).
7.4.2 Konditionale Effekte durch Zentrieren
Konditionale Effekte lassen sich ebenso für bestimmte Werte von metrischen Variablen berechnen. Nachfolgend schauen wir uns diese Effekte für die beiden Extremwerte der Voreinstellungsskale an. Dieser Schritt nennt sich Zentrierung. Dafür ist lediglich eine kleine Änderung am Code notwendig. Wir fügen lediglich ein I() samt dem gesuchten Wert (hier 1 oder 5) ein. I() verhindert, dass R die Zahl als Objekt interpretiert und eine Fehlermeldung ausgibt.
lm(gesamt ~ schwab * I(atol - 1), data = vb17) |> # atol = 1
report_table()Parameter | Coefficient | 95% CI | t(359) | p | Std. Coef. | Std. Coef. 95% CI | Fit
------------------------------------------------------------------------------------------------------------
(Intercept) | 4.08 | [ 3.65, 4.51] | 18.69 | < .001 | 0.10 | [-0.04, 0.24] |
schwab | -1.13 | [-1.69, -0.56] | -3.91 | < .001 | 0.06 | [-0.08, 0.20] |
atol - 1 | -0.12 | [-0.29, 0.06] | -1.30 | 0.196 | 0.09 | [-0.01, 0.19] |
schwab × atol - 1 | 0.40 | [ 0.17, 0.64] | 3.40 | < .001 | 0.18 | [ 0.07, 0.28] |
| | | | | | |
AIC | | | | | | | 926.81
AICc | | | | | | | 926.98
BIC | | | | | | | 946.29
R2 | | | | | | | 0.05
R2 (adj.) | | | | | | | 0.05
Sigma | | | | | | | 0.86Die Tabelle zeigt, dass sich der Interaktionsterm nicht ändert, der Haupteffekt für die Voreinstellung hingegen schon. Dieser Haupteffekt gilt nun für den Fall, dass der Befragte sehr negativ zur schwäbischen Mundart eingestellt ist. Erwartungsgemäß ist der Haupteffekt stark negativ (B = 1.13).
Das gleiche Spiel können wir mit dem anderen Extrempunkt der Skala machen.
lm(gesamt ~ schwab * I(atol - 5), data = vb17) |> # atol = 5
report_table()Parameter | Coefficient | 95% CI | t(359) | p | Std. Coef. | Std. Coef. 95% CI | Fit
-----------------------------------------------------------------------------------------------------------
(Intercept) | 3.62 | [ 3.30, 3.94] | 22.15 | < .001 | 0.47 | [-0.04, 0.99] |
schwab | 0.48 | [ 0.05, 0.92] | 2.20 | 0.029 | 0.76 | [ 0.25, 1.28] |
atol - 5 | -0.12 | [-0.29, 0.06] | -1.30 | 0.196 | 0.09 | [-0.01, 0.19] |
schwab × atol - 5 | 0.40 | [ 0.17, 0.64] | 3.40 | < .001 | 0.18 | [ 0.07, 0.28] |
| | | | | | |
AIC | | | | | | | 926.81
AICc | | | | | | | 926.98
BIC | | | | | | | 946.29
R2 | | | | | | | 0.05
R2 (adj.) | | | | | | | 0.05
Sigma | | | | | | | 0.86In dieser Konstellation finden wir einen positiven Effekt für Personen, die eine Sympathie für den schwäbischen Dialekt haben.
7.4.3 Conditional effects plot
Unsere gerade aufgestellten Berechnungen können wir auch für alle Werte der Voreinstellung zum Dialekt durchführen und grafisch darstellen. Dafür gibt es die Funktion plot_slopes().
marginaleffects::plot_slopes(m2_atol, variables = "schwab", condition = "atol") +
labs(x = "ATOL Score", y = "Effekt von Dialekt auf Bewertung") +
geom_hline(yintercept = 0, linetype = "dashed")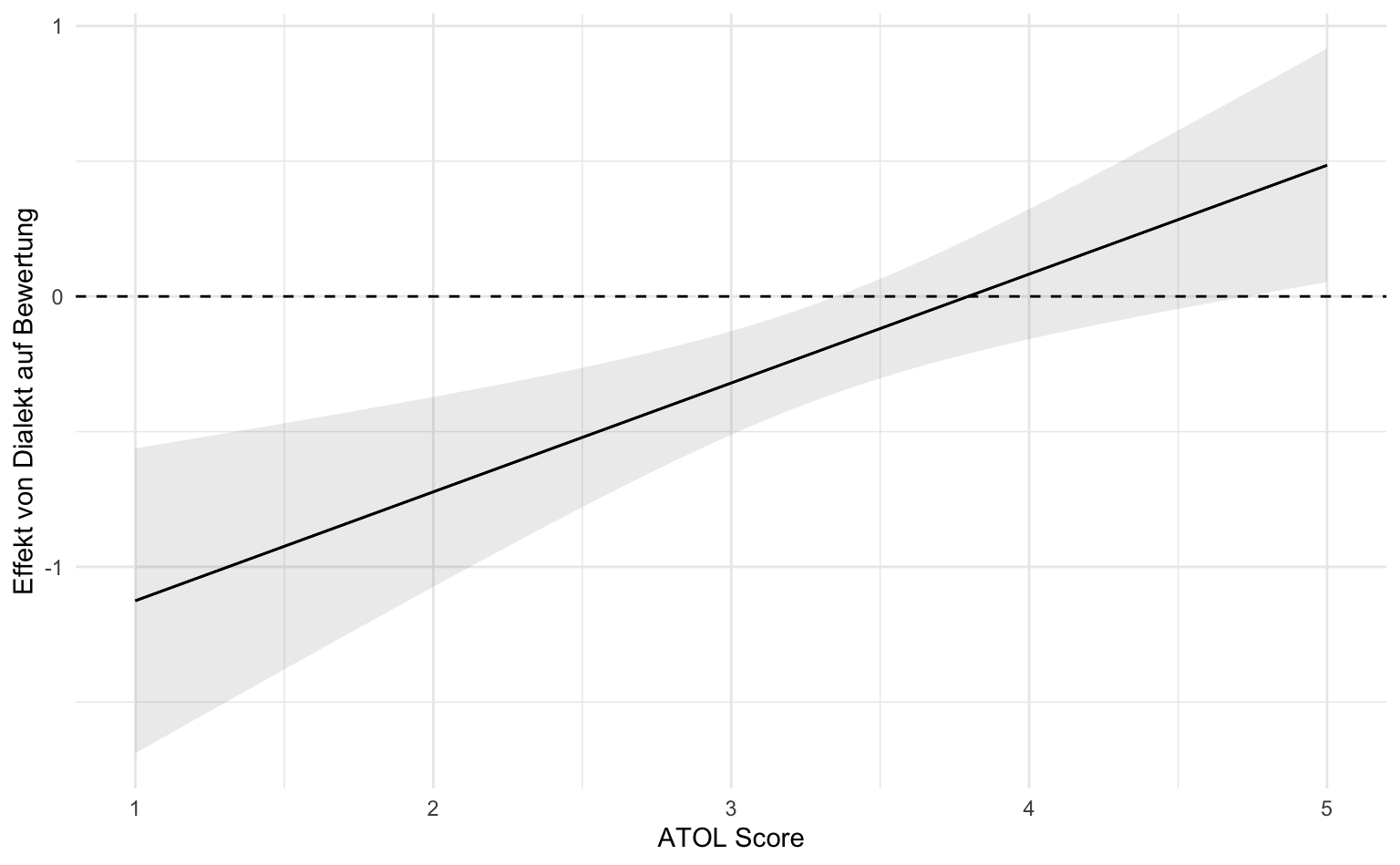
Die Grafik zeigt substantiell negative Effekte für Personen, die das Schwäbische eher ablehnen. Lediglich bei Liebhabern des Dialekts lassen sich leicht positive Effekte feststellen.
7.4.4 Modellvorhersagen (Dialekt und 3 Level von ATOL)
Die Modellvorhersagen lassen sich auch für bestimmte Ausprägungen der Prädiktoren berechnen.
preds_schwab_atol <- marginaleffects::avg_predictions(m2_atol, variables = list("schwab" = 0:1, "atol" = c(1, 3, 5))) |>
as_tibble()
preds_schwab_atol# A tibble: 6 × 9
schwab atol estimate std.error statistic p.value s.value conf.low conf.high
<int> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 0 1 4.08 0.218 18.7 5.92e- 78 257. 3.65 4.51
2 1 1 2.95 0.187 15.8 4.99e- 56 184. 2.59 3.32
3 0 3 3.85 0.0735 52.3 0 Inf 3.70 3.99
4 1 3 3.53 0.0643 54.8 0 Inf 3.40 3.65
5 0 5 3.62 0.163 22.1 1.10e-108 359. 3.30 3.94
# ℹ 1 more row7.4.5 Visualisierung der Vorhersagen
preds_schwab_atol |>
mutate(atol = factor(atol, labels = c("niedrig (1)", "mittel (3)", "hoch (5)"))) |>
ggplot(aes(
x = factor(schwab), y = estimate, ymin = conf.low, ymax = conf.high,
group = atol, color = atol,
)) +
geom_pointrange(position = position_dodge(.33)) +
geom_line(position = position_dodge(.33)) +
scale_x_discrete(labels = c("Hochdeutsch", "Dialekt")) +
labs(y = "Gesamtbewertung (vorhergesagt)", x = "Dialekt", color = "ATOL Score")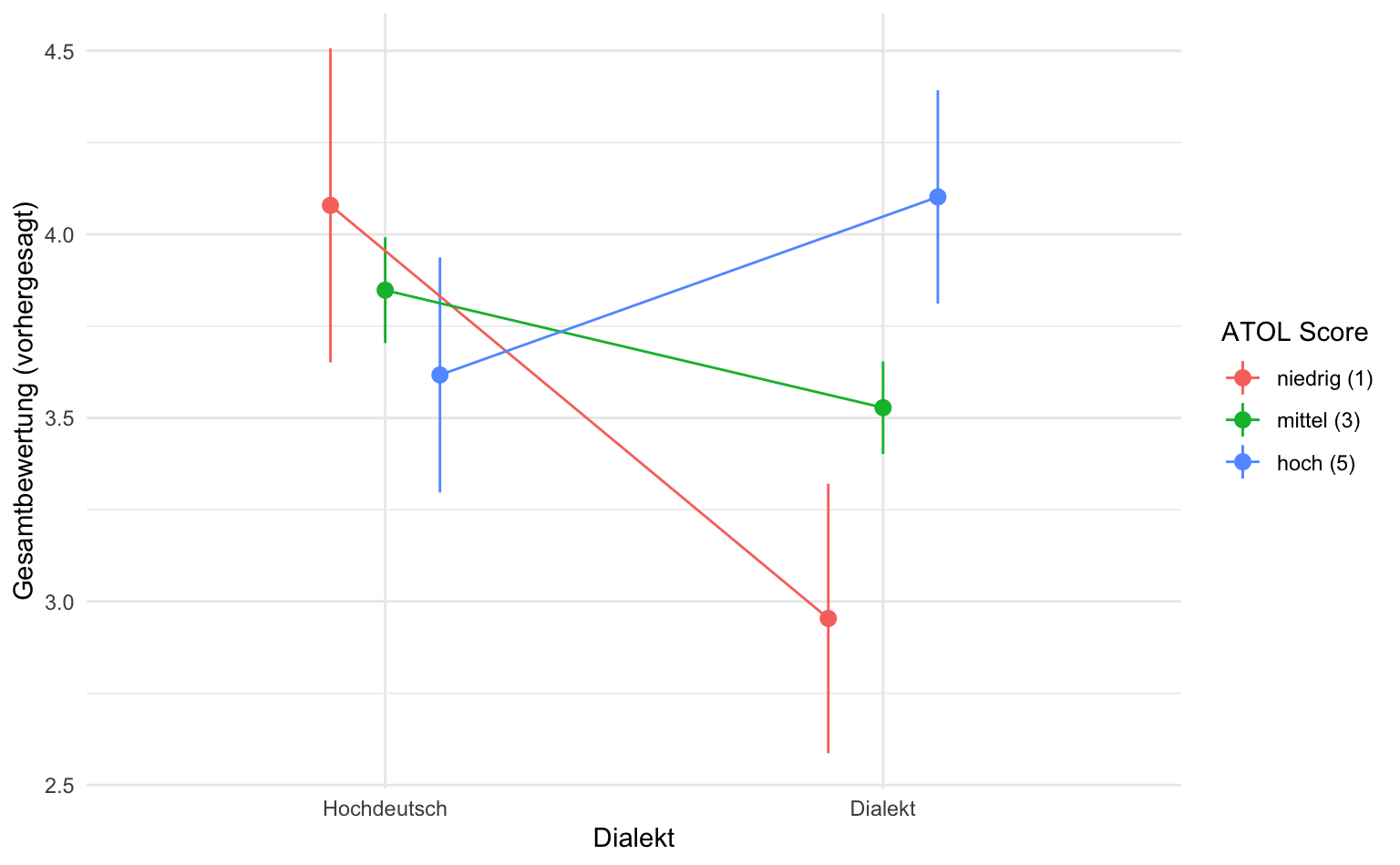
Die Visualisierung bestätigt unsere bereits angestellten Analysen. Je positiver die Voreinstellung gegenüber dem Schwäbischen, desto besser ist die vorhergesagte Bewertung des schwäbisch sprechenden Politikers. Zugleich zeigt sich, dass hochdeutsch sprechende Politiker besser bewertet werden.