6 Modellvorhersagen
Beispielanalyse
Welche Variablen sagen politisches Wissen voraus?
6.1 Pakete und Daten laden
Wir laden die üblichen Pakete und die Daten von van Erkel & van Aelst (2021). Wichtig für diese Übung ist vor allem das marginaleffects-Paket.
library(marginaleffects)
library(report)
library(tidyverse)
theme_set(theme_minimal())vanerkel21 <- haven::read_sav("data/Vanerkel_Vanaelst_2021.sav") |>
mutate(
Education = as_factor(Education),
Gender = as_factor(Gender)
) |>
haven::zap_labels()
vanerkel21# A tibble: 993 × 74
StartDate_w3 EndDate_w3 Duration__in_seconds_w3 Gender Year_of_birtg Age
<date> <date> <dbl> <fct> <dbl> <dbl>
1 2019-04-09 2019-04-09 440 female 29 45
2 2019-04-09 2019-04-09 504 female 43 59
3 2019-04-06 2019-04-06 610 female 36 52
4 2019-04-03 2019-04-03 414 female 7 23
5 2019-04-09 2019-04-09 1274 female 7 23
# ℹ 988 more rows
# ℹ 68 more variables: Education <fct>, News_channels_w3_1 <dbl>,
# News_channels_w3_2 <dbl>, News_channels_w3_3 <dbl>,
# News_channels_w3_4 <dbl>, News_channels_w3_5 <dbl>,
# News_channels_w3_6 <dbl>, Political_interest <dbl>, StartDate_w4 <date>,
# EndDate_w4 <date>, Duration__in_seconds__w4 <dbl>,
# News_channels_w4_1 <dbl>, TV <dbl>, Newspaper <dbl>, Websites <dbl>, …6.2 Regressionsmodell
Als Ausgangspunkt nehmen wir dasselbe Modell wie in der vorangegangen Übung.
m1 <- lm(PK ~ Gender + Age + Education + Political_interest, data = vanerkel21)
report::report_table(m1)Parameter | Coefficient | 95% CI | t(987) | p | Std. Coef. | Std. Coef. 95% CI | Fit
--------------------------------------------------------------------------------------------------------------
(Intercept) | 0.46 | [ 0.09, 0.83] | 2.45 | 0.014 | -0.13 | [-0.27, 0.02] |
Gender [female] | -0.51 | [-0.65, -0.37] | -6.96 | < .001 | -0.37 | [-0.48, -0.27] |
Age | 0.02 | [ 0.02, 0.03] | 8.48 | < .001 | 0.23 | [ 0.17, 0.28] |
Education [Middle] | 0.35 | [ 0.13, 0.56] | 3.15 | 0.002 | 0.26 | [ 0.10, 0.41] |
Education [High] | 0.60 | [ 0.38, 0.82] | 5.42 | < .001 | 0.44 | [ 0.28, 0.60] |
Political interest | 0.20 | [ 0.18, 0.23] | 14.76 | < .001 | 0.40 | [ 0.35, 0.45] |
| | | | | | |
AIC | | | | | | | 3021.38
AICc | | | | | | | 3021.49
BIC | | | | | | | 3055.69
R2 | | | | | | | 0.35
R2 (adj.) | | | | | | | 0.34
Sigma | | | | | | | 1.106.3 Modellvorhersagen mit kategoriellem Prädiktor
6.3.1 Vorhersagen nach Geschlecht
Um aus Regressionsmodellen in R Vorhersagen zu generieren, gibt es die eingebaute predict()-Funktion, die aber im Umgang etwas mühsam ist. Mit der Funktion avg_predictions() aus dem marginaleffects-Paket erhalten wir für eine oder mehrere Prädiktorvariablen vorhergesagte Werte des Outcomes. Dabei werden für kategorielle Variablen die Vorhersagen für jede Ausprägung aggregiert, für metrische über (typische) Einzelwerte. Wir speichern die Vorhersagen im Tibble preds_gender (preds = predictions).
preds_gender <- marginaleffects::avg_predictions(m1, variables = "Gender") |>
as_tibble()
preds_gender# A tibble: 2 × 8
Gender estimate std.error statistic p.value s.value conf.low conf.high
<fct> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 female 2.78 0.0519 53.5 0 Inf 2.68 2.88
2 male 3.29 0.0495 66.4 0 Inf 3.19 3.38Für die weiblichen Befragten wird ein Wert von 2,78 für politisches Wissen durch das Modell vorhergesagt (Spalte estimate), für männliche Befragte ein höherer Wert von 3,29. Die Differenz entspricht dem Regressionskoeffizienten für die Geschlechtsvariable B = -0.51 (siehe Regressionstabelle oben). Für die Vorhersagen erhalten wir zusätzlich auch ein 95%-Konfidenzintervall (Spalten conf.low und conf.high).
6.3.2 Visualisierung nach Geschlecht
Da die avg_predictions()-Funktion einen Tibble zurückliefert, können wir diesen direkt als Daten für eine ggplot Grafik verwenden. Wir legen die Geschlechtsvariable auf die X-Achse, die vorhergesagten Werte samt Unter- und Obergrenze auf die Y-Achse. Mit geom_pointrange() werden die Punktschätzer und Konfidenzintervalle dargestellt.
preds_gender |>
ggplot(aes(x = Gender, y = estimate, ymin = conf.low, ymax = conf.high)) +
geom_pointrange() +
labs(x = "Gender", y = "Predicted political knowledge")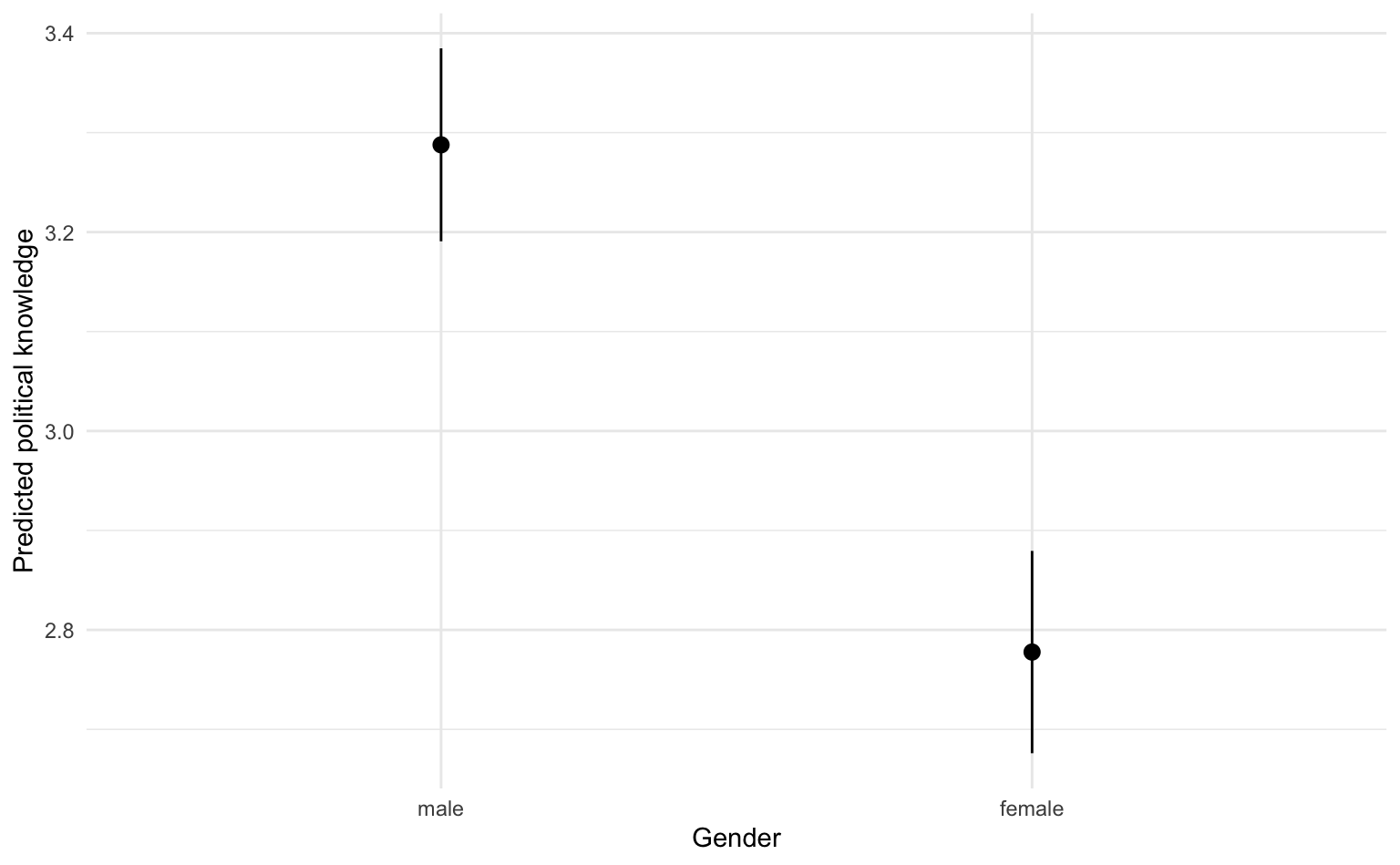
Da sich die Konfidenzintervalle nicht überschneiden, können wir sofort sagen, dass der Unterschied zwischen männlichen und weiblichen Befragten hinsichtlich politischem Wissen statistisch signifikant ist, auch unter Kontrolle von Bilder, Alter und pol. Interesse.
6.4 Modellvorhersagen mit mehreren kategoriellen Prädiktoren
Statt über eine können wir die Vorhersagen auch über mehrere Prädiktorvariablen aggregieren, hier über Geschlecht und Bildung.
preds_gender_edu <- marginaleffects::avg_predictions(m1, variables = c("Gender", "Education")) |>
as_tibble()
preds_gender_edu# A tibble: 6 × 9
Gender Education estimate std.error statistic p.value s.value conf.low
<fct> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 female Middle 2.71 0.0672 40.3 0 Inf 2.58
2 male Middle 3.22 0.0650 49.5 0 Inf 3.09
3 female High 2.96 0.0633 46.8 0 Inf 2.84
4 male High 3.47 0.0645 53.8 0 Inf 3.35
5 female Lower 2.36 0.106 22.2 1.80e-109 361. 2.15
# ℹ 1 more row
# ℹ 1 more variable: conf.high <dbl>Der daraus resultierenden Datensatz hat 2 (Geschlecht) x 3 (Bildung) = 6 Zeilen für alle Kombinationen der Variablen.
6.4.1 Visualisierung nach Geschlecht und Bildung
Wie oben visualisieren wir die Vorhersagen mit geom_pointrange(), diesmal allerdings gruppiert und farblich unterschieden nach den drei Bildungsgruppen. Mit dem position_dodge(.5)-Argument werden die Punkte+Intervalle etwas versetzt statt direkt übereinander dargestellt.
preds_gender_edu |>
ggplot(aes(
x = Gender, y = estimate, ymin = conf.low, ymax = conf.high,
group = Education, color = Education
)) +
geom_pointrange(position = position_dodge(.5)) +
labs(x = "Gender", y = "Predicted political knowledge")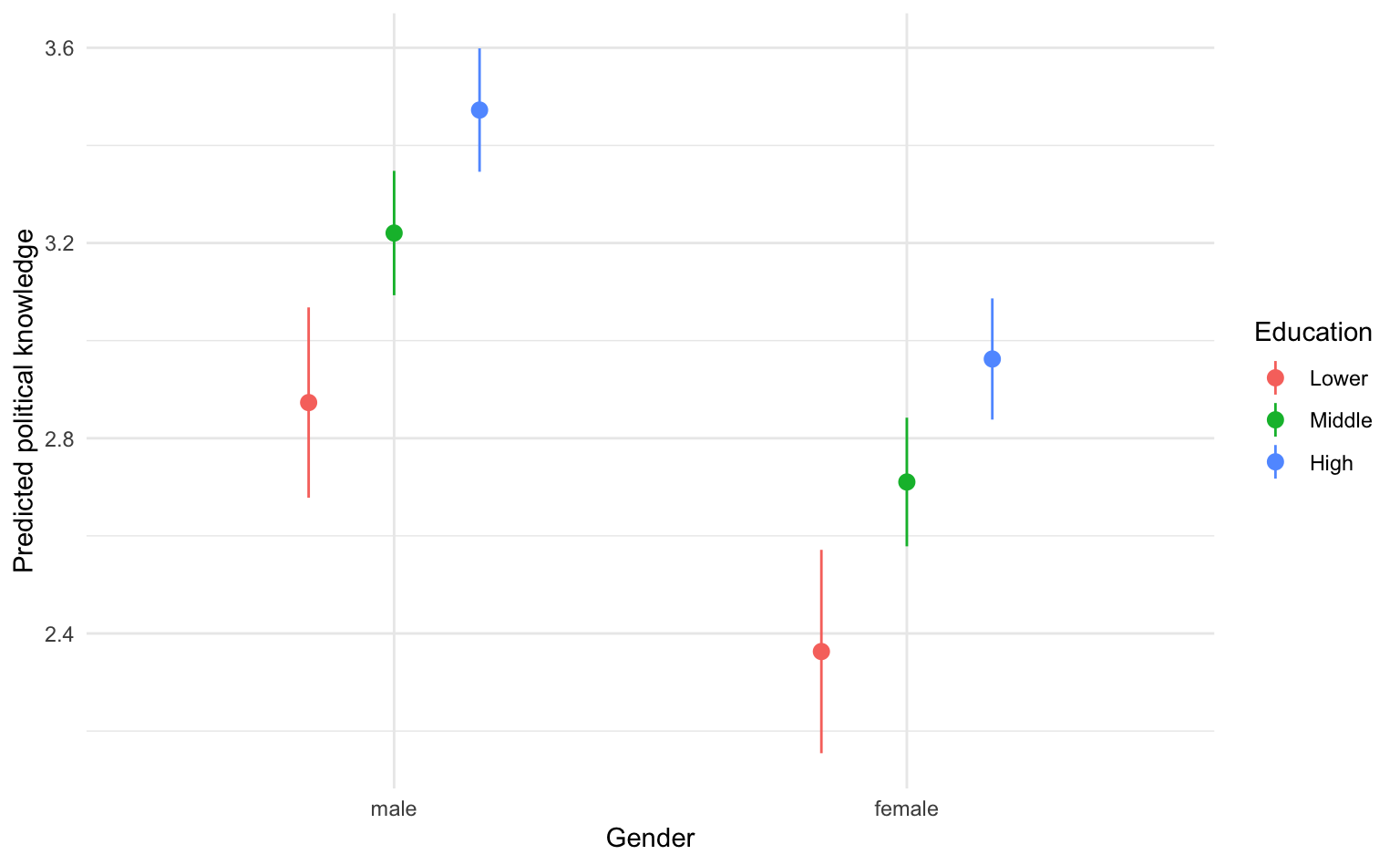
Da das Regressionsmodell nur die Haupteffekte von Bildung und Geschlecht enthält, aber nicht deren Interaktionseffekt (siehe die Sitzung zu Moderationsanalyse), sind die Abstände in den Vorhersagen zwischen den Bildungsgruppen bei Männern und Frauen gleich (bzw. die Abstände zwischen Männern und Frauen pro Bildungsgruppe).
6.5 Modellvorhersagen mit metrischem Prädiktor
6.5.1 Vorhersage nach Alter
Für metrische Variablen ist der Code identisch, die Funktion avg_predictions() erkennt selbständig, ob es sich um metrische oder kategorielle Variablen handelt. Bei metrischen Prädiktoren werden standardmäßig fünf typische Werte ausgewählt.
preds_age <- marginaleffects::avg_predictions(m1, variables = "Age") |>
as_tibble()
preds_age# A tibble: 5 × 8
Age estimate std.error statistic p.value s.value conf.low conf.high
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 19 2.29 0.0951 24.1 1.12e-128 425. 2.11 2.48
2 44 2.85 0.0421 67.6 0 Inf 2.76 2.93
3 56 3.11 0.0359 86.7 0 Inf 3.04 3.18
4 65 3.31 0.0470 70.5 0 Inf 3.22 3.40
5 71 3.44 0.0585 58.8 0 Inf 3.33 3.56Warum genau diese Werte für Alter? Dies sind die “five numbers” nach Tukey, die auch für die Visualisierung von Boxplots verwendet werden: Minium, erstes Quartil, Median, drittes Quartil, Maximum. Diese kann man in R mit der Funktion fivenum() erhalten.
fivenum(vanerkel21$Age)[1] 19 44 56 65 716.5.2 Vorhersage mit spezifischen Werten
Wollen wir Vorhersagen für andere Werte der Altersvariable erhalten, müssen wir den Funktionsaufruf leicht modifizieren. Das variables-Argument ist nun eine benannte Liste. Hier wollen wir statt fivenum die eingebaute threenum Variante, d.h. Mittelwert plus/minus 1 SD. Weitere Beispiele finden sich in der Hilfe für avg_predictions().
marginaleffects::avg_predictions(m1, variables = list("Age" = "threenum")) |>
as_tibble()# A tibble: 3 × 8
Age estimate std.error statistic p.value s.value conf.low conf.high
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 39.0 2.74 0.0504 54.2 0 Inf 2.64 2.84
2 53.0 3.04 0.0350 86.9 0 Inf 2.98 3.11
3 66.9 3.35 0.0504 66.5 0 Inf 3.25 3.45Zu guter letzt können wir auch direkt sagen, für welche Werte für Vorhersagen erhalten wollen, wir übergeben einfach einen Zahlenvektor, hier für die Werte 18, 40 und 65.
marginaleffects::avg_predictions(m1, variables = list("Age" = c(18, 40, 65))) |>
as_tibble()# A tibble: 3 × 8
Age estimate std.error statistic p.value s.value conf.low conf.high
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 18 2.27 0.0975 23.3 3.75e-120 397. 2.08 2.46
2 40 2.76 0.0486 56.7 0 Inf 2.66 2.85
3 65 3.31 0.0470 70.5 0 Inf 3.22 3.406.5.3 Visualisierung nach Alter
Die Vorhersagen für metrische Prädiktoren lassen sich am besten als Regressionsgerade samt Konfidenzband visualisieren, d.h. geom_line() und geom_ribbon(). Das Konfidenzband wird fast transparent dargestellt (alpha = .1). Auf der X-Achse ist wieder die Prädiktorvariable, auf der Y-Achse die vorhergesagten Werte.
preds_age |>
ggplot(aes(
x = Age, y = estimate, ymin = conf.low, ymax = conf.high
)) +
geom_ribbon(alpha = .1) +
geom_line() +
labs(x = "Age", y = "Predicted political knowledge")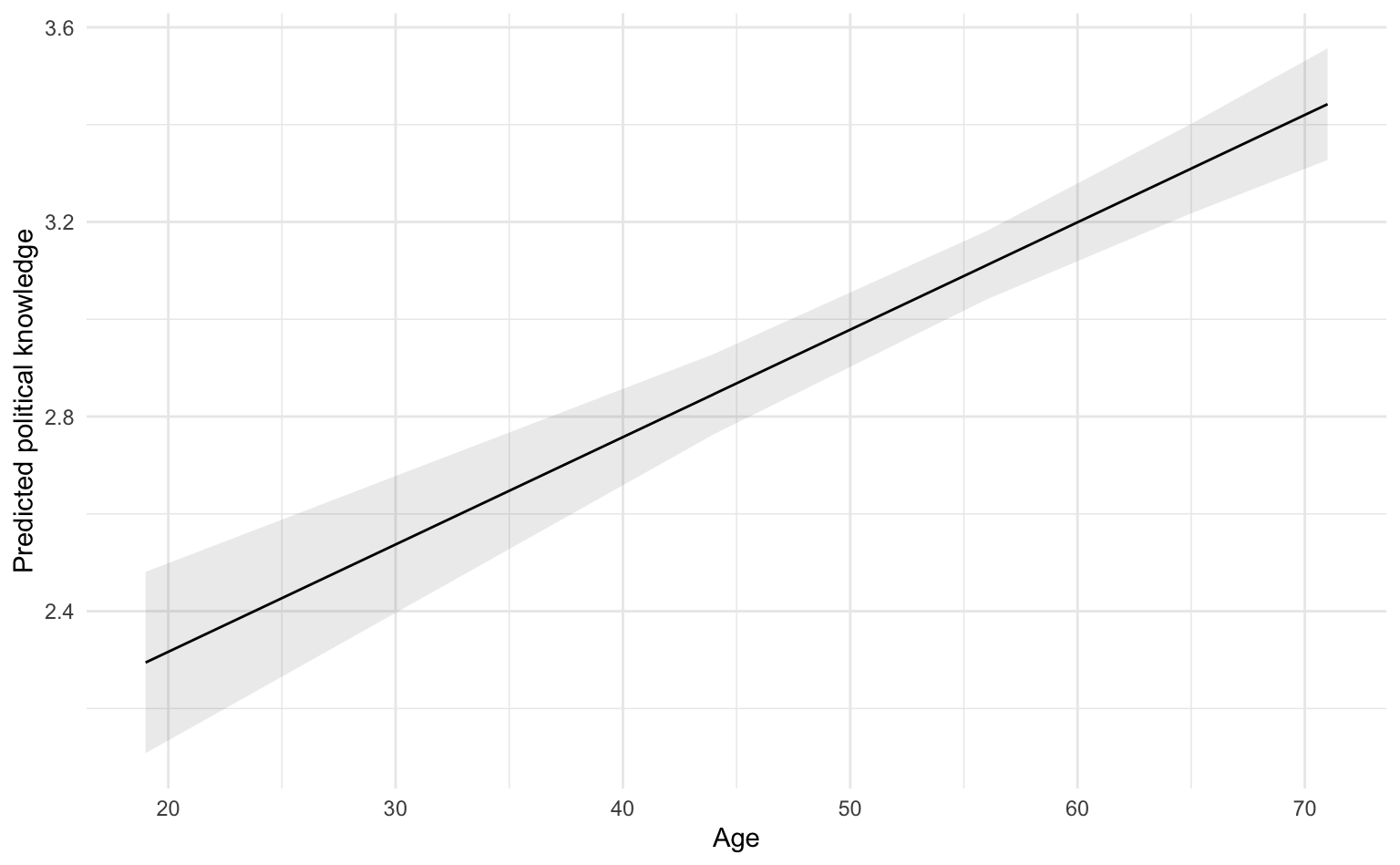
Dies entspricht auch dem, was wir mit geom_smooth() in der ersten Übung zur Regression gesehen haben.
6.6 Modellvorhersagen mit kategoriellen und metrischen Prädiktoren
6.6.1 Vorhersagen nach Alter und Geschlecht
Zuletzt kombinieren wir die Vorhersagen für Alter und Geschlecht.
preds_age_gender <- marginaleffects::avg_predictions(m1, variables = c("Age", "Gender")) |>
as_tibble()
preds_age_gender# A tibble: 10 × 9
Age Gender estimate std.error statistic p.value s.value conf.low conf.high
<dbl> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 19 female 2.03 0.0969 20.9 3.11e- 97 321. 1.84 2.22
2 19 male 2.54 0.106 23.9 3.55e-126 417. 2.33 2.75
3 44 female 2.58 0.0543 47.5 0 Inf 2.47 2.69
4 44 male 3.09 0.0571 54.1 0 Inf 2.98 3.20
5 56 female 2.84 0.0534 53.2 0 Inf 2.74 2.95
# ℹ 5 more rowsWir erhalten einen Datensatz mit 5 (Alter) x 2 (Geschlecht) = 10 Zeilen.
6.6.2 Visualisierung nach Alter und Geschlecht
Der Plot ist grundsätzlich mit demjenigen für Alter identisch, wir fügen lediglich die aesthetics für Farbe und Füllung nach Geschlecht hinzu.
preds_age_gender |>
ggplot(aes(
x = Age, y = estimate, ymin = conf.low, ymax = conf.high,
group = Gender, fill = Gender, color = Gender
)) +
geom_ribbon(alpha = .1, color = NA) +
geom_line() +
labs(x = "Age", y = "Predicted political knowledge")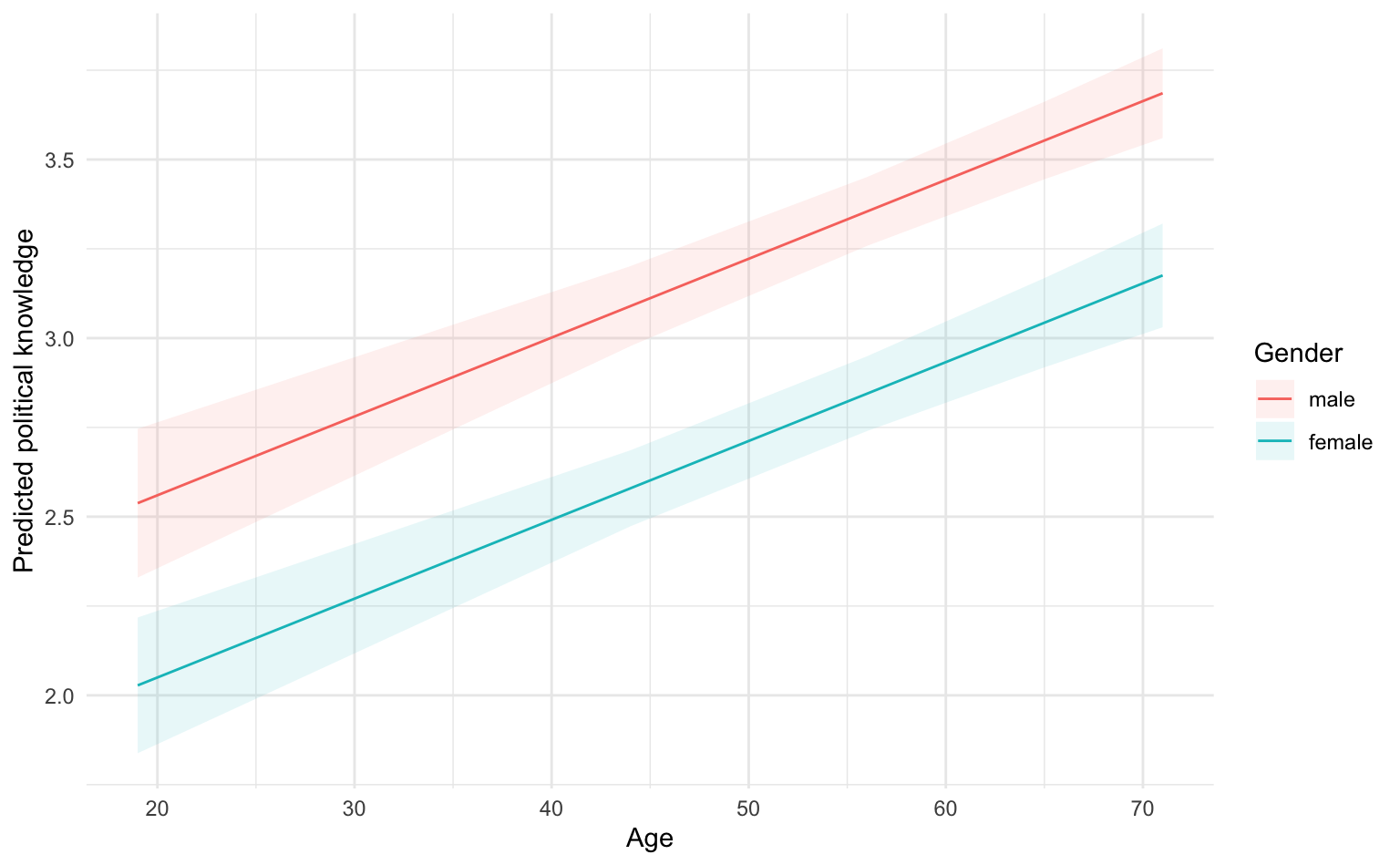
Da wieder nur die Haupteffekte von Alter und Geschlecht um Modell enthalten sind, sehen wir zwei parallele Regressionsgeraden, d.h. der Alterseffekt ist bei Männern und Frauen gleich, aber die Achsenabschnitte unterscheiden sich. Das wird in der Übung zur Moderationsanalyse anders aussehen.