10 Varianzanalyse

Wir laden das report- und das tidyverse-Paket und öffnen den Datensatz des Victim Blaming-Experiments.

library(report)
library(tidyverse)
theme_set(theme_minimal())
vb <- readxl::read_excel("data/victim_blaming.xlsx")

10.1 Gruppenmittelwerte

Mit der Varianzanalyse überprüfen wir den Einfluss einer Gruppen- bzw. Faktor-Variable (kategorial, also nominal oder ordinal mit wenigen Ausprägungen) auf eine metrische Variable, wobei im Gegensatz zum t-Test mehr als zwei Gruppen verglichen werden können. Im Zusammenhang mit der Varianzanalyse spricht man oft von abhängiger (= zu erklärender) und unabhängiger (=erklärende) Variable, auch wenn wir diese Kausalität nicht immer aus den Daten herleiten können. Der Grund ist, dass die Varianzanalyse sehr häufig aus Auswertungsmethode bei Experimenten Einsatz findet.

In unserem Experiment ist eine der zentralen Annahmen, dass sich die Selbstdarstellung des Opfers (stimulus_rec) auf das Ausmaß an Victim Blaming und damit zusammenhängend auch auf das Mitgefühl mit dem Opfer (v_11) auswirkt.

Zunächst nutzen wir die Funktionen group_by() und summarise(), um Mittelwert, Standardabweichung und Fallzahl für die Variablev_11 basierend auf den Gruppen der Variable stimulus_rec auszugeben. Den gleichen Code haben wir bereits beim t-Test für unabhängige Stichproben verwendet.

vb |>
  group_by(stimulus_rec) |>
  summarise(
    v_11_mean = mean(v_11, na.rm = TRUE),
    v_11_sd = sd(v_11, na.rm = TRUE),
    n = n()
  )

# A tibble: 4 × 4
  stimulus_rec            v_11_mean v_11_sd     n
  <chr>                       <dbl>   <dbl> <int>
1 Extravertiert mit Info       3.89   0.943   153
2 Extravertiert ohne Info      4.15   0.812   137
3 Introvertiert mit Info       3.91   0.864   139
4 Introvertiert ohne Info      4.11   0.773   157

Wir sehen, dass in der Stichprobe die Mittelwerte in beiden Experimentalbedingungen mit wenig Informationspreisgabe etwas höher sind als bei den Stimulusvarianten mit viel Informationspreisgabe, in allen Gruppen aber generell recht hoch. D.h. die Mittelwerte zeigen an, dass die Teilnehmer:innen viel Mitleid mit dem Opfer hatten, etwas mehr, wenn dieses weniger von sich preisgegeben hat.

10.2 Varianzanalyse

Die einfaktorielle Varianzanalyse dient dazu, Unterschiede in den Gruppenmittelwerten der abhängigen Variable v_11 basierend auf den Kategorien der faktoriellen Variable stimulus_rec zu untersuchen.

Nullhypothese H0: Der Mittelwert des Mitleids mit dem Opfer ist in allen Experimentalbedingungen gleich.

Wir verwenden die Funktion aov(), um die einfaktorielle Varianzanalyse durchzuführen. Die grundlegende Syntax lautet: aov(metrische_variable ~ gruppen_variable, data = Datenframe). Wir führen die Varianzanalyse durch und speichern das Ergebnis im Objekt results_anova.

results_anova <- aov(v_11 ~ stimulus_rec, data = vb)
results_anova

Call:
   aov(formula = v_11 ~ stimulus_rec, data = vb)

Terms:
                stimulus_rec Residuals
Sum of Squares        7.8464  421.0154
Deg. of Freedom            3       582

Residual standard error: 0.8505258
Estimated effects may be unbalanced

Der Ergebnisoutput ist nicht besonders informativ, wir erhalten lediglich Quadratsummen und Freiheitsgrade. Deshalb verwenden wir wieder die report_table()-Funktion, um die Ergebnisse der Varianzanalyse in einer übersichtlichen Tabelle darzustellen. Diese enthält neben F-Wert, Freiheitsgraden und p-Wert auch das Effektstärkemaß Eta².

results_anova |>
  report_table()

Parameter    | Sum_Squares |  df | Mean_Square |    F |     p | Eta2 |  Eta2 95% CI
-----------------------------------------------------------------------------------
stimulus_rec |        7.85 |   3 |        2.62 | 3.62 | 0.013 | 0.02 | [0.00, 1.00]
Residuals    |      421.02 | 582 |        0.72 |      |       |      |

In unserem Fall zeigt sich, dass sich die Experimentalgruppen statistisch signifikant hinsichtlich ihres Mitleids mit dem Opfer unterscheiden (F(3, 582) = 3.62, p < .05), wobei das Modell mit 2% Varianzaufklärung (Eta² = 0.02) eine geringe Vorhersagekraft des Antwortverhaltens hat.

Die Varianzanalyse gibt nur Aufschluss darüber, ob sich mindestens zwei der Gruppen signifikant voneinander unterscheiden. Vergleichen wir nur zwei Gruppen, reicht uns dieses Ergebnis schon. Vergleichen wir aber mehr als zwei Gruppen, wollen wir auch wissen welche Gruppen sich signifikant voneinander unterscheiden. Hierfür benötigen wir Post-Hoc-Tests.

10.3 Post-Hoc Tests

Um zu ermitteln, welche Gruppen sich signifikant voneinander unterscheiden, werden mithilfe eines Post-Hoc-Tests paarweise Vergleiche zwischen den Gruppenmittelwerten durchgeführt. Für die Durchführung des Post-Hoc-Tests stehen sehr viele Möglichkeiten zur Verfügung, wir empfehlen zunächst Tukey Honest Significant Difference-Test (Tukey’s HSD), bei dem eine Alphafehler-Korrektur stattfindet.

Mit der TukeyHSD()-Funktion wird der Tukey’s HSD durchgeführt, wobei der Funktion das Modell results_anova übergeben wird.

results_anova |>
  TukeyHSD()

  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = v_11 ~ stimulus_rec, data = vb)

$stimulus_rec
                                                       diff          lwr
Extravertiert ohne Info-Extravertiert mit Info   0.26439578  0.006641813
Introvertiert mit Info-Extravertiert mit Info    0.02478018 -0.231993603
Introvertiert ohne Info-Extravertiert mit Info   0.21939137 -0.029550344
Introvertiert mit Info-Extravertiert ohne Info  -0.23961561 -0.503430446
Introvertiert ohne Info-Extravertiert ohne Info -0.04500442 -0.301202525
Introvertiert ohne Info-Introvertiert mit Info   0.19461119 -0.060600752
                                                       upr     p adj
Extravertiert ohne Info-Extravertiert mit Info  0.52214975 0.0418875
Introvertiert mit Info-Extravertiert mit Info   0.28155395 0.9945986
Introvertiert ohne Info-Extravertiert mit Info  0.46833308 0.1061375
Introvertiert mit Info-Extravertiert ohne Info  0.02419923 0.0902747
Introvertiert ohne Info-Extravertiert ohne Info 0.21119369 0.9691164
Introvertiert ohne Info-Introvertiert mit Info  0.44982313 0.2026629

Ob sich die verschiedenen Gruppenpaarungen signifikant voneinander unterscheiden, lesen wir in der letzten Spalte p adj ab. In unserem Fall unterscheiden sich die Bedingung Extravertiert ohne Info (p < .05) statistisch signifikant von der Bedingung Extravertiert mit Info, näherungsweise signifikant (p < .10) ist auch der Unterschied zwischen Extravertiert ohne Info und Introvertiert mit Info. Das Ergebnise ist somit - was aufgrund der geringen Varianzerklärung schon zu erwarten war - nicht sehr eindeutig, spricht aber dafür, dass eher die Manipulation der Informationspreisgabe einen Einfluss hatte und weniger die der Persönlichkeit - wie auch aus den Mittelwertunterschieden oben zu sehen.

Was ist eine Alphafehler-Korrektur und welche weiteren Post-Hoc-Tests gibt es?

Ein Alphafehler ist das Ablehnen der Nullhypothese, obwohl sie wahr ist. Man nimmt also fälschlicherweise an, dass ein Zusammenhang/Unterschied besteht, obwohl dies nicht zutrifft. Bei unserem üblichen Signifikanzniveau von \(\alpha\) = .05 bedeutet das, dass 5% aller Tests signifikant sein werden, selbst wenn die Nullhypothese gilt. Eine Korrektur des Alphafehlers ist immer dann notwendig, wenn wir mehrere Tests mit der gleichen Stichprobe durchführen. Führen wir beispielsweise 20 Tests durch, wird erwartungsgemäß einer fälschlicherweise signifikant. Die Wahrscheinlichkeit für einen Alphafehler für alle Tests zusammen beträgt also nicht mehr 5%, sondern ist deutlich höher (Alphafehler-Inflation). Diesem Problem kann man z.B. mit dem Tukey’s HSD entgegenwirken.

Alternativ zum Tukey-Test können auch über die Funktion pairwise.t.test(abhängige_variable, fator_variable, p.adj='bonferroni') paarweise t-Tests durchgeführt werden. Das Argument p.adj='bonferroni' stellt sicher, dass die p-Werte entsprechend dem Verfahren von Bonferroni angepasst werden, um das Problem der multiplen Tests zu berücksichtigen. Neben der Bonferroni-Korrektur lassen sich zahlreiche andere Verfahren über p.adj einstellen, siehe dazu die Übersicht in der Hilfe von ?p.adjust.

pairwise.t.test(vb$v_5f, vb$stimulus_rec, p.adj = "bonferroni")


    Pairwise comparisons using t tests with pooled SD 

data:  vb$v_5f and vb$stimulus_rec 

                        Extravertiert mit Info Extravertiert ohne Info
Extravertiert ohne Info 0.35                   -                      
Introvertiert mit Info  <2e-16                 <2e-16                 
Introvertiert ohne Info <2e-16                 <2e-16                 
                        Introvertiert mit Info
Extravertiert ohne Info -                     
Introvertiert mit Info  -                     
Introvertiert ohne Info 0.56                  

P value adjustment method: bonferroni

Interpretation und Beschreibung

Insgesamt haben die Teilnehmer:innen viel Mitleid mit dem Opfer (M_{Extravertiert_mitInfo}= 3.89, SD_{Extravertiert_mitInfo}= 0.94; M_{Extravertiert_ohneInfo}= 4.15, SD_{Extravertiert_ohneInfo}= 0.81, M_{Introvertiert_mitInfo}= 3.91, SD_{Introvertiert_mitInfo}= 0.86; M_{Introvertiert_ohneInfo}= 4.11, SD_{Introvertiert_ohneInfo}= 0.77). Dabei gibt es einen schwachen, aber signifikanten Zusammenhang zwischen der Experimentalbedingung und dem Ausmaß an Mitleid mit dem Opfer (F(3, 582) = 3.62, p < .05, Eta² = 0.02). Allerdings unterscheiden sich nur die Bedingungen Extravertiert ohne Info und Extravertiert mit Info statistisch signifikant voneinander (Tukey’s HSD, p < .05), tendenziell auch Extravertiert ohne Info und Introvertiert mit Info (Tukey’s HSD, p < .10). Das Ergebnis spricht insgesamt dafür, dass eher die Manipulation der Informationspreisgabe einen Einfluss hatte und weniger die der Persönlichkeit - wie auch aus den Mittelwertunterschieden ersichtlich. Der Effekt ist aber schwach ausgeprägt.

10.4 Visualisierung

Für die Visualisierung der Gruppenunterschiede als Boxplots können wir genau den gleichen Code wie beim t-Test verwenden - die Anzahl der Gruppen spielt hierfür keine Rolle. Allerdings zeigt sich hier das Problem, dass die Medianwerte der Gruppen sich im Gegensatz zu den Mittelwerten nicht unterscheiden:

vb |>
  ggplot(aes(x = stimulus_rec, y = v_11)) +
  geom_boxplot() +
  labs(x = "Versuchsbedingung", y = "Mitleid")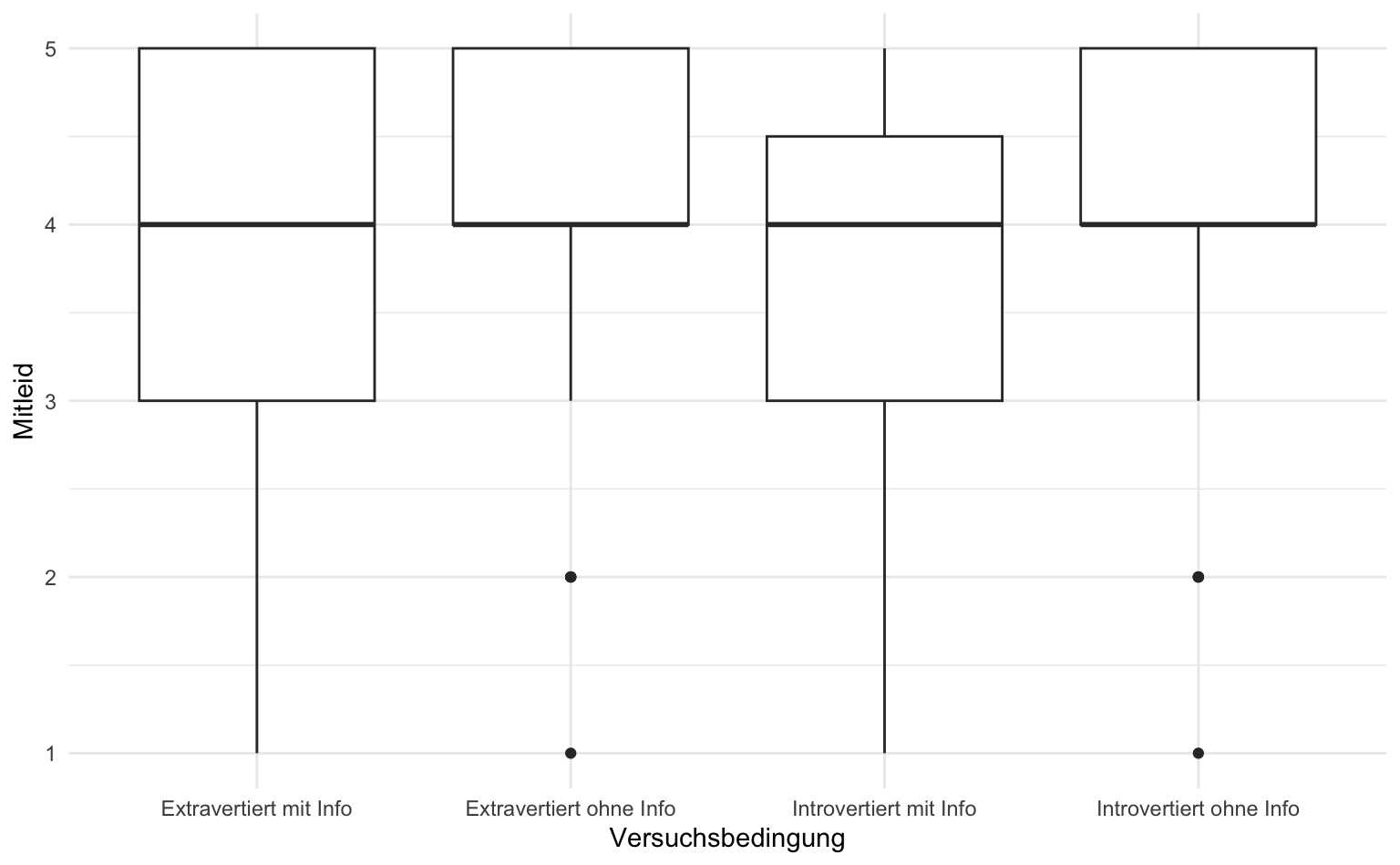

Alternativ könnten wir daher die Mittelwerte und dazugehörigen Konfidenzintervalle pro Gruppe darstellen. Hierfür eignet sich stat_summary() mit den Parametern fun.data und geom. Für erstere legen wir fest, dass wir den Mittelwert samt Konfidenzintervall (confidence limits = cl) pro Gruppe berechnen möchten. Als Darstellung eignet sich pointrange, d.h. Punkte und dazugehörige Linien bis zu den Intervallgrenzen. In der Literatur findet man diese Darstellung unter dem Namen caterpillar oder forest plot.

Achtung: Der Wertebereich ist nun deutlich enger, weil keine einzelnen Daten, sondern nur die berechneten Intervalle darstellt werden. Falls uns die Y-Achse irreführend eng erscheint, können wir die Grenzen der Y-Achse noch etwas anpassen, siehe die Funktion coord_cartesian() mit dem Argument ylim in der letzen Codezeile.

vb |>
  ggplot(aes(x = stimulus_rec, y = v_11)) +
  stat_summary(fun.data = mean_cl_boot, geom = "pointrange") +
  labs(x = "Versuchsbedingung", y = "Mitleid (Mittelwert und 95% CI)") +
  coord_cartesian(ylim = c(3.5, 4.5))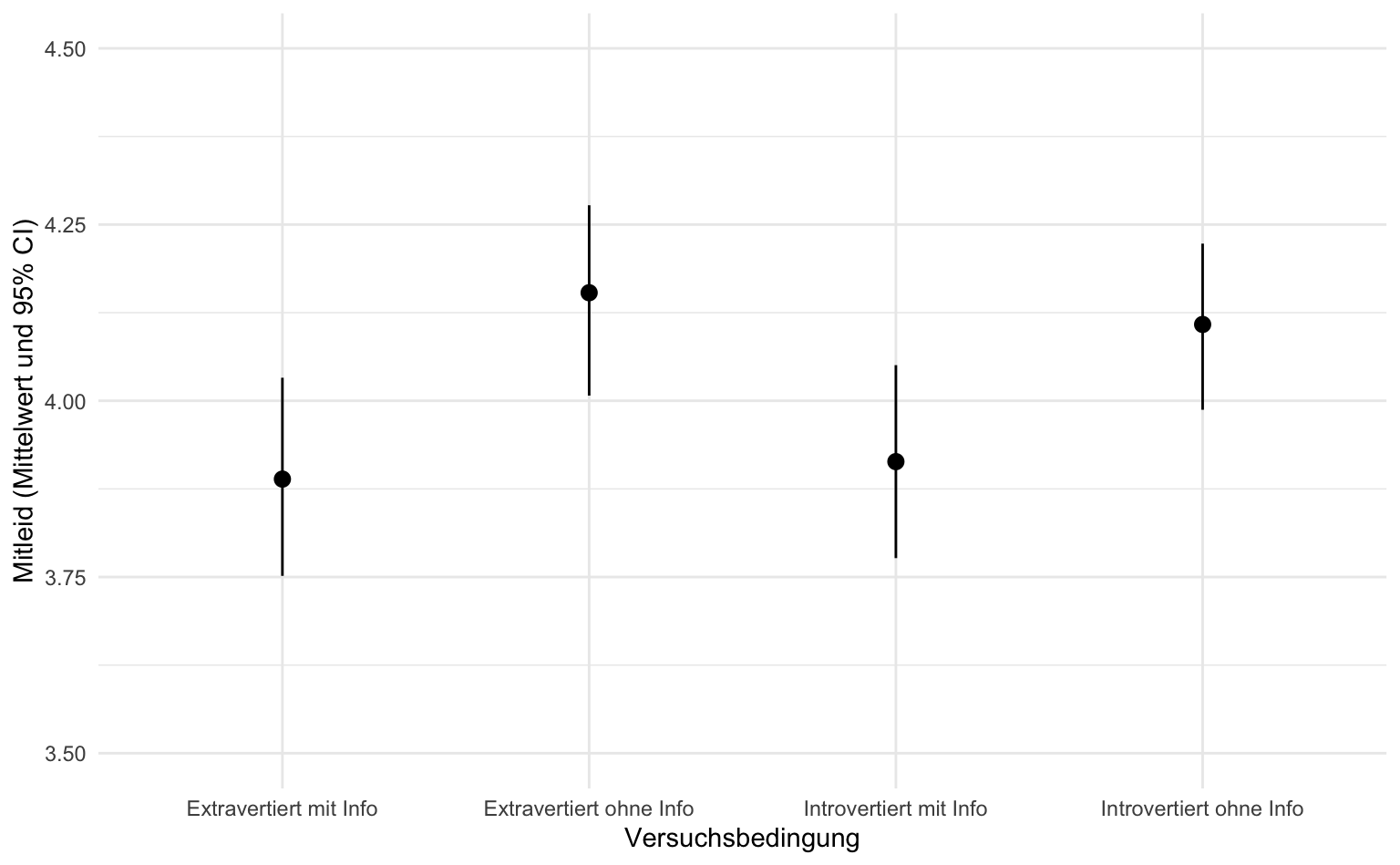

10.5 Glossar

Funktion	Definition
aov()	Berechnen des F-Tests
TukeyHSD()	Berechnen des Tukey’s HSD Post-Hoc-Tests im Anschluss an die Varianzanalyse

10.6 Hausaufgabe

Für die Hausaufgabe analysieren wir den Datensatz gewohnheiten.xlsx.

Unterscheiden sich Personen verschiedener Bildungsniveaus (p_4rec) darin wie sehr sie den Fernseher und die Zeitung vermissen würden? Falls ja: Wie groß ist der Erklärungsanteil und welche der drei Gruppen unterscheiden sich signifikant voneinander?
Unterscheiden sich Personen verschiedener Bildungsniveaus darin in ihrer Gesamteinstellung gegenüber dem Fernsehen? Die Einstellung gegenüber dem Fernsehen wird über die Items f_einst1, f_einst2, f_einst3, f_einst4 gemessen, wobei hohe Werte eher Ablehnung bedeuten. Falls ja: Wie groß ist der Erklärungsanteil und welche der drei Gruppen unterscheiden sich signifikant voneinander?

Für alle Aufgaben gilt:

Geben Sie als Kommentar (mit # beginnend) an, welche Frage Sie bearbeiten, darunter folgt der zugehörige Code.
Betrachten Sie zunächst die Variablen univariat.
Führen Sie dann die bivariate(n) Analyse(n) durch und beschreiben und interpretieren deren Ergebnisse.
Die Antwortsätze folgen darunter, ebenfalls als Kommentar (mit # beginnend).