9 t-Tests

Wir laden das report und das tidyverse-Paket und öffnen den Datensatz des Victim Blaming Experiments.

library(report)
library(tidyverse)
theme_set(theme_minimal())
vb <- readxl::read_excel("data/victim_blaming.xlsx")

9.1 Arten von t-Tests

Es gibt verschiedene Varianten des t-Tests, die sich in R alle mit der Funktion t.test() durchführen lassen. In jedem Fall gilt, dass das Datenniveau der Variablen, die wir vergleichen/testen wollen, metrisch sein muss.

t-Test bei einer Stichprobe: Vergleich eines Mittelwertes gegen einen festen kritischen Wert ➜ Ist der Wert größer/kleiner als ein fester kritischer Wert?
t-Test bei verbundenen Stichproben: Vergleich von zwei verschiedenen Mittelwerten, die von denselben Fällen (z.B. Befragten) stammen ➜ Gibt es einen Unterschied zwischen zwei verschiedenen Variablen?
t-Test bei unabhängigen Stichproben: Vergleich der Mittelwerte einer Variablen zwischen zwei Gruppen ➜ Unterscheiden sich die Mittelwerte der Variablen zwischen den beiden Gruppen?

Der mit Abstand häufigste Anwendungsfall ist der t-Test bei unabhängigen Stichproben. Dieser eignet sich, wenn wir eine Gruppierungsvariable haben, die nominales Datennivau aufweist und nur zwei Ausprägungen hat (bei mehr als zwei Ausprägungen benötigen wir eine Varianzanalyse).

Gerichtete Hypothesen und einseitiges Testen

In den Beispielen unten testen wir immer ungerichtete Unterschiedshypothesen, während im Forschungsalltag oft gerichtete Hypothesen (Mittelwert in Gruppe A ist kleiner als in Gruppe B, Mittelwert von \(x1\) ist größer als Mittelwert von \(x2\), etc.) interessanter sind. In der Praxis ergeben sich bei gerichteten Hypothesen zwei Unterschiede:

Wenn sich schon die Stichprobenmittelwerte nicht hypothesenkonform unterscheiden, nehmen wir die Nullhypothese an.
Wenn die Unterschiede hypothesenkonform sind, dürfen wir die p-Werte vor der Interpretation halbieren.

9.2 t-Test bei einer Stichprobe

Bei diesem t-Test prüfen wir, ob sich der Mittelwert einer Variable \(x\) von einem Vergleichswert \(\mu\) unterscheidet. In diesem Fall ist unsere Forschungsfrage: Weicht der Mittelwert des Victim Bamings (vb_index) von der Skalenmitte (3) ab?

Nullhypothese H0: Der wahre Mittelwert in der Grundgesamtheit ist die Skalenmitte 3 (kein Unterschied)

Zunächst schauen wir uns den Mittelwert und die Standardabweichung der Variable an.

vb |>
  summarise(
    m_vb = mean(vb_index, na.rm = TRUE),
    sd_vb = sd(vb_index, na.rm = TRUE)
  )

# A tibble: 1 × 2
   m_vb sd_vb
  <dbl> <dbl>
1  1.76 0.643

Der Mittelwert in der Stichprobe weicht schon einmal deutlich von der Skalenmitte 3 ab. Kann dies ggf. nur am Stichprobenfehler liegen? Wir prüfen dies mit dem t-Test bei einer Stichprobe, der folgendermaßen aufgebaut ist:

t.test(Datenframe$variable, mu = Zahlenwert)

In unserem Fall gilt: \(mu=3\).

t.test(vb$vb_index, mu = 3)


    One Sample t-test

data:  vb$vb_index
t = -46.856, df = 585, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 3
95 percent confidence interval:
 1.703117 1.807463
sample estimates:
mean of x 
  1.75529

Der Output zeigt zunächst den t-Wert, die Freiheitsgrade und den p-Wert. Zudem werden Mittelwert und Konfidenzintervall für vb_index angezeigt. Etwas übersichtlicher wird es durch die Funktion report_table() aus dem report-Paket, das eine Vielzahl von Tests einheitlich mit allen notwendigen Angaben in Tabellenform darstellt. Wir können per Pipe direkt das Ergebnis von t.test() weitergeben.

t.test(vb$vb_index, mu = 3) |>
  report_table()

One Sample t-test

Parameter   | Mean |   mu | Difference |       95% CI | t(585) |      p | Cohen's d |  Cohen's d  CI
----------------------------------------------------------------------------------------------------
vb$vb_index | 1.76 | 3.00 |      -1.24 | [1.70, 1.81] | -46.86 | < .001 |     -1.94 | [-2.07, -1.80]

Alternative hypothesis: two.sided

Wie können wir die Ergebnisse interpretieren?

Der p-Wert ist kleiner .05, d.h. statistisch signifikant. Wenn in der Grundgesamtheit der Mittelwert \(\mu=3\) gilt, ist es extrem unwahrscheinlich (p < .001), den Mittelwert von 1.76 in unserer Stichprobe zu erhalten. Wir lehnen daher die Nullhypothese ab.
Zu derselben Testentscheidung kommen wir auch, wenn wir das 95%-CI betrachten. Der kritische Wert von 3 ist darin nicht enthalten. Da wir wissen, dass Konfidenzintervalle in 95% aller Fälle den Populationswert enthalten, gehen wir davon aus, dass 3 nicht der Populationsmittelwert ist. Wir lehnen daher die Nullhypothese ab.
Neben der statistischen Signifikanz sollten wir auch immer die substanzielle Stärke des Unterschieds betrachten. Hierfür können wir Cohen’s d heranziehen. Cohen’s d ist ein Maß der Effektstärke, ähnlich Cramer’s V bei der Kreuztabelle. Cohen’s d gibt an, wie viele Standardabweichungen die beiden Mittelwerte auseinanderliegen - je größe der Betrag, desto größer/bedeutsamer also der Unterschied. Ein negatives Vorzeichen zeigt an, dass der erste Wert kleiner als der zweite ist (in unserem Fall: \(x\) kleiner als \(\mu\)), ein positives Vorzeichen zeigt an, dass der erste Wert größer als der zweite ist. In unserem Beispiel zeigt der Wert von Cohen’s d (-1.94), dass der Mittelwert fast 2 Standardabweichungen unter \(\mu=3\) liegt, ein sehr großer Unterschied.

Interpretation und Beschreibung

Der Mittelwert der Variable Victim Blaming weicht stark und statistisch signifikant von der theoretischen Skalenmitte 3 ab (t(585) = -46.86; p < .001, Cohen’s d = -1.94). Insgesamt betreiben die Teilnehmer:innen der Studie wenig Victim Blaming (M = 1.76, SD = 0.64).

9.3 t-Test bei verbundenen Stichproben

Beim t-Test für verbundene Stichproben vergleichen wir zwei Variablen miteinander. Dies können zwei verschiedene Variablen oder dieselbe Variable zu unterschiedlichen Messzeitpunkten, z.B. vor und nach einer Experimentalmanipulation, sein. Technisch funktioniert der t-Test bei verbundenen Stichproben wie der t-Test bei einer Stichprobe: Es wird im Hintergrund die Differenz der beiden Variablen \(x1\) und \(x2\) gebildet, also zeilenweise \(x1-x2\), und diese Differenz wird darauf getestet, ob sie 0 ist.

Konkret fragen wir in diesem Beispiel: Glauben die Befragten eher, dass das Cybermobbing-Opfer Selbstvertrauen (v_15e) verliert oder dass es depressiv (v_15f) wird?

Nullhypothese: Es gibt keinen Unterschied zwischen der Erwartung, dass das Opfer Selbstvertrauen verliert und dass es depressiv wird, d.h. die Differenz beider Variablen ist 0.

Zunächst schauen wir uns wieder für beide Variablen die Mittelwerte und Standardabweichungen an. Zusätzlich interessieren wir uns noch für die Differenz der Mittelwerte, da diese ja für den Test verwendet wird.

vb |>
  summarise(
    m_selbstvertrauen = mean(v_15e, na.rm = TRUE),
    sd_selbstvertrauen = sd(v_15e, na.rm = TRUE),
    m_depressiv = mean(v_15f, na.rm = TRUE),
    sd_depressiv = sd(v_15f, na.rm = TRUE),
    m_differenz = mean(v_15e - v_15f, na.rm = TRUE)
  )

# A tibble: 1 × 5
  m_selbstvertrauen sd_selbstvertrauen m_depressiv sd_depressiv m_differenz
              <dbl>              <dbl>       <dbl>        <dbl>       <dbl>
1              4.18              0.941        3.00         1.01        1.19

Wir sehen, dass die Proband:innen eher glauben, dass das Opfer Selbstvertrauen verliert (M = 4.18) als dass es depressiv wird (M = 3.00), die Differenz beträgt mehr als einen Skalenpunkt, was auf einer Skala von 1-5 recht viel ist.

Nun testen wir, ob dieser Unterschied nur durch den Stichprobenfehler zu erklären ist. Hierfür führen wir den t-Test bei verbundenen Stichproben durch. Wie schon beim t-Test bei einer Stichprobe, nutzen wir für die übersichtliche und vollständige Darstellung report_table().

t.test(vb$v_15e, vb$v_15f, paired = TRUE) |>
  report_table()

Paired t-test

Parameter |    Group | Difference | t(585) |      p |       95% CI | Cohen's d | Cohen's d  CI
----------------------------------------------------------------------------------------------
vb$v_15e  | vb$v_15f |       1.19 |  26.33 | < .001 | [1.10, 1.28] |      1.09 |  [0.99, 1.19]

Alternative hypothesis: two.sided

Fehlende Werte

Achtung: Der report_table()-Befehl funktioniert nur, wenn es keine Fälle gibt, bei denen eine der beiden Variablen einen fehlenden Wert aufweist. Ist dies der Fall, dann müssen die fehlenden Werte vorher ausgeschlossen werden.

vb_ohne_na <- vb |>
  drop_na(v_15e, v_15f) # Alternativ: filter(!is.na(v_15e) & !is.na(v_15f))

t.test(vb_ohne_na$v_15e, vb_ohne_na$v_15f, paired = TRUE) |>
  report_table()

Paired t-test

Parameter        |            Group | Difference | t(585) |      p |       95% CI | Cohen's d | Cohen's d  CI
-------------------------------------------------------------------------------------------------------------
vb_ohne_na$v_15e | vb_ohne_na$v_15f |       1.19 |  26.33 | < .001 | [1.10, 1.28] |      1.09 |  [0.99, 1.19]

Alternative hypothesis: two.sided

Wie können wir die Ergebnisse interpretieren?

Der p-Wert ist kleiner .05, d.h. statistisch signifikant. Wenn in der Grundgesamtheit beide Variablen denselben Wert hätten, sich also nicht unterscheiden würden, ist es extrem unwahrscheinlich (p < .001), einen Mittelwertunterschied von 1.19 in unserer Stichprobe zu erhalten. Wir lehnen daher die Nullhypothese ab.
Zu derselben Testentscheidung kommen wir auch, wenn wir das 95%-CI der Differenz der beiden Mittelwerte betrachten. Dieses enthält nicht die 0, die uns sagen würde, dass es keinen Mittelwertunterschied zwischen den beiden Variablen gibt. Wir lehnen daher die Nullhypothese ab.
Auch hier interessiert uns die Effektstärke. Cohen’s d = -1.09, unsere beiden Mittelwerte liegen also etwa eine Standardabweichung auseinander, das ist ein deutlicher Unterschied.

Interpretation und Beschreibung

Die Teilnehmer:innen glauben eher, dass das Cybermobbing-Opfer an Selbstvertrauen verliert als dass es depressiv wird (M_{Selbstvertrauen} = 4.18, SD_{Selbstvertrauen} = 0.94; M_Depressiv = 3.00, SD_Depressiv = 1.01). Der Unterschied ist signifikant und groß (t(585) = 26.33; p < .001, Cohen’s d = -1.09).

9.4 t-Test bei unabhängigen Stichproben

Beim t-Test für unabhhängige Stichproben wird geprüft, ob zwei Gruppen sich im Mittelwert von einer Variable x unterscheiden. Konkret fragen wir: Unterscheiden sich diejenigen, die das Profil mit vielen Infos (info) gesehen haben, von denen, die das Profil mit wenigen Infos gesehen haben, im Mittelwert des Victim Blamings (vb_index)?

Nullhypothese H0: Diejenigen Teilnehmer:innen, die das Profil mit vielen Infos gesehen haben, unterscheiden sich im Mittelwert von Victim Blaming nicht von denen, die das Profil mit wenigen Infos gesehen haben (kein Unterschied).

Zunächst betrachten wir wieder die Stichprobenkennwerte Mittelwert und Standardabweichung für vb_index, diesmal gruppiert nach der Variable info. Zusätzlich betrachten wir noch die Gruppengröße n, um zu prüfen, ob jede Gruppe ausreichend Fälle beinhaltet.

vb |>
  group_by(info) |>
  summarise(
    mean_vb = mean(vb_index, na.rm = TRUE),
    sd_vb = sd(vb_index, na.rm = TRUE),
    n = n()
  )

# A tibble: 2 × 4
  info      mean_vb sd_vb     n
  <chr>       <dbl> <dbl> <int>
1 mit Info     1.82 0.661   292
2 ohne Info    1.69 0.620   294

Wir sehen, dass beide Gruppen mit über 290 Personen ungefährt gleich (wie beim Experiment zu erwarten) und ausreichend besetzt sind. Zudem sehen wir auch Unterschiede in den Mittelwerten: Diejenigen, die das Profil mit vielen Infos gesehen haben, betreiben etwas mehr Victim Blaming als die, die das Profil mit wenigen Infos gesehen haben. Der Mittelwertunterschied ist aber recht gering, er beträgt nur 0.14 Skalenpunkte.

Wir prüfen nun anhand eines t-Tests bei unabhängigen Stichproben, ob dieser Unterschied der Nullhypothese widerspricht und nutzen zur Ergebnisdarstellung wieder report_table().

t.test(metrische_variable ~ gruppen_variable, data = Datenframe)

t.test(vb_index ~ info, data = vb) |>
  report_table()

Welch Two Sample t-test

Parameter | Group | Mean_Group1 | Mean_Group2 | Difference |       95% CI | t(581.08) |     p |    d |        d  CI
-------------------------------------------------------------------------------------------------------------------
vb_index  |  info |        1.82 |        1.69 |       0.13 | [0.02, 0.23] |      2.38 | 0.018 | 0.20 | [0.03, 0.36]

Alternative hypothesis: two.sided

Wie können wir die Ergebnisse interpretieren?

Der p-Wert ist kleiner .05, d.h. statistisch signifikant. Wenn sich in der Grundgesamtheit die beiden Gruppen nicht unterscheiden würden, ist es unwahrscheinlich (p = .018), die Mittelwerte aus unserer Stichprobe zu erhalten. Wir lehnen daher die Nullhypothese ab.
Zu derselben Testentscheidung kommen wir auch, wenn wir das 95%-CI der Differenz der beiden Mittelwerte betrachten. Dieses enthält nicht die 0 - wenn auch ganz knapp nicht -, die uns sagen würde, dass es keinen Mittelwertunterschied zwischen den beiden Variablen gibt. Wir lehnen daher die Nullhypothese ab.
Auch hier interessiert uns die Effektstärke. Cohen’s d = 0.20, unsere beiden Mittelwerte liegen also nur 0.2 Standardabweichungen auseinander, das ist ein kleiner Unterschied.

Interpretation und Beschreibung

Die Teilnehmer:innen die das Profil mit vielen Infos gesehen haben, betreiben signifikant mehr Victim Blaming als diejenigen, die das Profil mit wenigen Infos gesehen haben (t(581,08) = 2.38; p < .05). Allerdings ist in beiden Gruppen Victim Blaming eher schwach ausgeprägt (M_mitInfo= 1.82, SD_mitInfo= 0.66; M_ohneInfo= 1.69, SD_ohneInfo= 0.62) und der Unterschied fällt auch klein aus (Cohen’s d = 0.20).

Hinweis zu Freitheitsgraden mit Nachkommastelle

Vielleicht ist Ihnen aufgefallen, dass die Freiheitsgrade beim t-Test bei unabhängigen Stichproben Nachkommastellen haben. Das liegt daran, dass R standardmäßig den Welch-Test rechnet, der für ungleiche Varianzen in den beiden Gruppen (eigentlich eine Anwendungsvoraussetzung für den t-Test) korrigiert und dieser korrigiert auch die Zahl der Freiheitsgrade. Das ist in den meisten Fällen völlig ok für uns. Wenn wir den exakten t-Test durchführen wollen, können wir t.test(..., var.equal = TRUE) verwenden.

t.test(vb_index ~ info, data = vb, var.equal = TRUE) |>
  report_table()

Two Sample t-test

Parameter | Group | Mean_Group1 | Mean_Group2 | Difference |       95% CI | t(584) |     p |    d |        d  CI
----------------------------------------------------------------------------------------------------------------
vb_index  |  info |        1.82 |        1.69 |       0.13 | [0.02, 0.23] |   2.38 | 0.018 | 0.20 | [0.03, 0.36]

Alternative hypothesis: two.sided

9.5 Visualisierung

Unterschiede zwischen zwei oder mehr Gruppen lassen sich am einfachsten über einen Boxplot visualisieren. Dabei gilt es zu beachten, dass nicht das arithmetische Mittel, sondern der Median der jeweiligen Gruppe als horizontale Linie dargestellt wird. Das ist in den meisten Fällen unproblematisch, solange Mittelwert und Median nicht so stark voneinander abweichen, dass t-Test und Visualisierung unterschiedliche Ergebnisse suggerieren.

vb |>
  ggplot(aes(x = info, y = vb_index)) +
  geom_boxplot() +
  labs(x = "Versuchsbedingung", y = "Victim Blaming")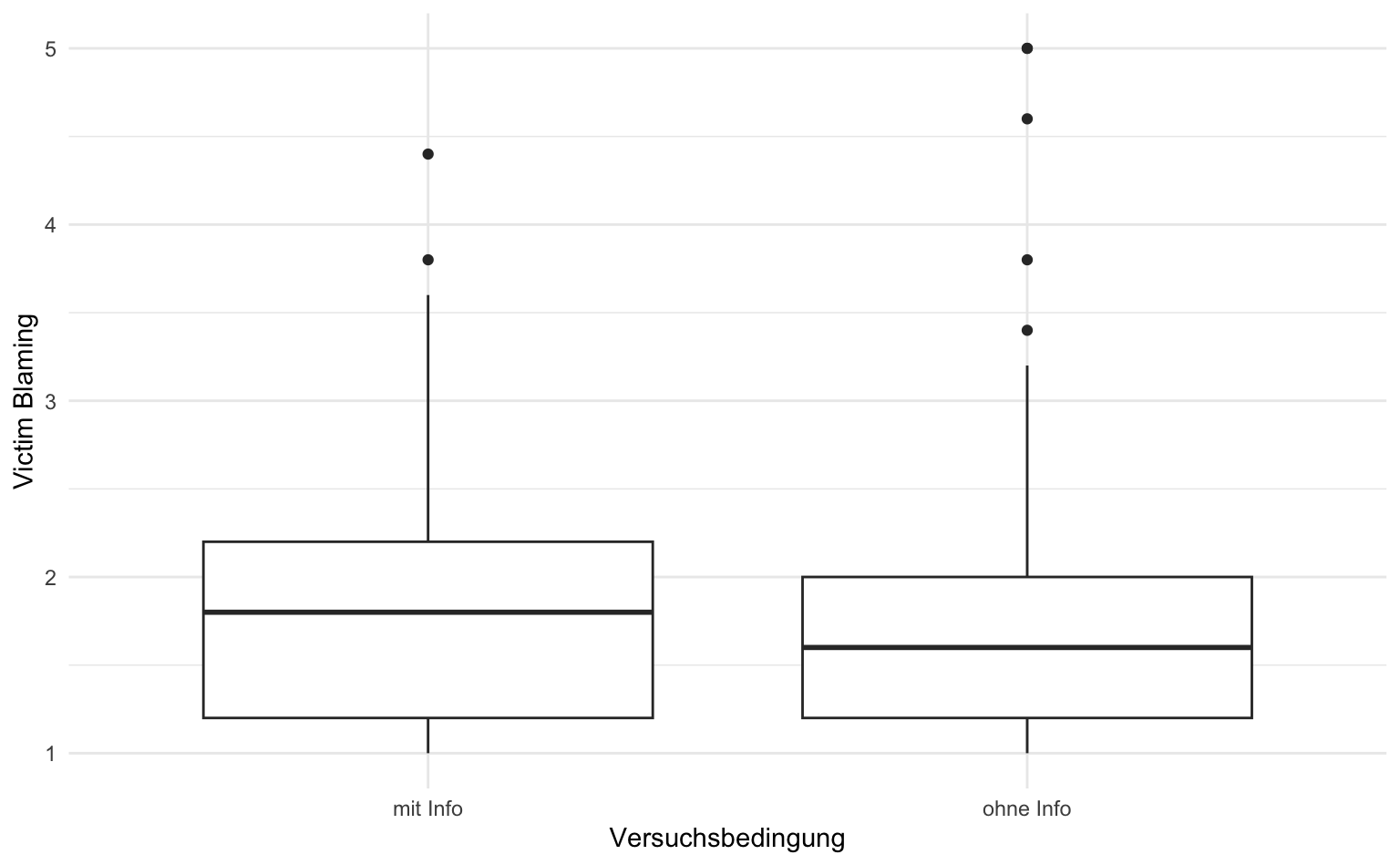

Die Boxen geben den Bereich an, in dem die mittleren 50% aller Werte liegen. Das untere Ende der Boxen ist also jeweils das erste Quartil und das obere Ende das dritte Quartil. Unterhalb der Boxen liegen also 25% der Werte, in den Boxen 50% aller Werte und über den Boxen 25% aller Werte.

Die senkrechten Linien gehen bis zu dem letzten Punkt, der noch im 1,5-fachen des Interquartilsabstands liegt. Das können alle vorkommenden Werte sein (wie es in unserem Beispiel unterhalb der Boxen der Fall ist). Wenn es sogenannte Ausreißer gibt, also Werte, die ungewöhnlich weit von den anderen Werte wegliegen, dann endet die Linie vorher und die Ausreißer werden durch Punkte dargestellt - wie es in unserem Beispiel oberhalb der Boxen der Fall ist.

9.6 Glossar

Funktion	Definition
group_by()	Einteilung des Dataframes/Tibbles in Gruppen anhand der angegebenen Variable(n)
report_table()	Erstellen einer Ergebnis-Tabelle aus einem statistischen Modell
t.test()	Berechnen aller drei Arten von t-Tests

9.7 Hausaufgabe

Für die Hausaufgabe analysieren wir den Datensatz gewohnheiten.xlsx.

Unterscheiden sich Männer und Frauen darin, wie sehr sie die tagesaktuellen Medien Fernseher, Zeitung und Radio vermissen würden?
Würden die Befragten den Fernseher oder das Smartphone stärker vermissen?

Für alle Aufgaben gilt:

Geben Sie als Kommentar (mit # beginnend) an, welche Frage Sie bearbeiten, darunter folgt der zugehörige Code.
Betrachten Sie zunächst die Variablen univariat.
Führen Sie dann die bivariate(n) Analyse(n) durch und beschreiben und interpretieren deren Ergebnisse.
Die Antwortsätze folgen darunter, ebenfalls als Kommentar (mit # beginnend).