library(report)
library(tidyverse)
theme_set(theme_minimal())
tg <- read_tsv("data/telegram.tsv")8 Kreuztabellen
Wir laden erstmals das report-Paket, das wir für die Ergebnisdarstellung vieler statistischer Tests und Analysen verwenden. Dieses muss ggf. erst installiert werden, was RStudio auch vorschlägt. Außerdem laden wir das tidyverse-Paket und öffnen den Datensatz der Telegram-Inhaltsanalyse.
8.1 Einfache Häufigkeiten
In dieser Übung wollen wir den Zusammenhang von ideologischer Ausrichtung eines Telegram-Kanals und den Zielen, die dort kommuniziert werden, untersuchen. Beide Variablen sind kategoriell (nominal oder ordinal mit wenigen Ausprägungen), so dass eine Kreuztabelle und ein Chi-Quadrat-Test für die Beantwortung unserer Frage sinnvoll sind. Zunächst schauen wir uns die beiden Variablen für sich genommen an, um ein erstes Gefühl für deren Verteilung zu entwickeln. Dafür verwenden wir wieder die count()-Funktion.
Zuerst zählen wir, wieviele Nachrichten von den Kanälen mit verschiedenen Ideologien stammen.
tg |>
count(ideologie) |>
mutate(percent = n / sum(n) * 100) |> # Prozentwerte
arrange(desc(n))# A tibble: 3 × 3
ideologie n percent
<chr> <int> <dbl>
1 Rechte 6240 54.7
2 Querdenken 2630 23.1
3 Verschwörung 2535 22.2Die zweite Variable, die uns interessiert, ist das kommunizierte Ziel ziel_1.
tg |>
count(ziel_1) |>
mutate(percent = n / sum(n) * 100) |> # Prozentwerte
arrange(desc(n)) |>
print(n = 20)# A tibble: 10 × 3
ziel_1 n percent
<dbl> <int> <dbl>
1 -9 5760 50.5
2 1 1693 14.8
3 2 1460 12.8
4 6 931 8.16
5 -1 574 5.03
6 3 558 4.89
7 4 308 2.70
8 7 50 0.438
9 8 39 0.342
10 5 32 0.281Hier fallen uns zwei Dinge auf: Erstens sind noch fehlende Werte (alle negativen Zahlen) in den Daten vorhanden, zweitens hat die Variable sehr viele Ausprägungen (das Tibble hat 10 Zeilen), manche mit sehr kleinen Fallzahlen. Dies wird eine Kreuztabelle sehr schwer lesbar machen (3 Spalten x 8 Zeilen!), und vermutlich auch die Annahmen des Chi-Quadrat-Tests über minimale erwartete Zellgrößen (Daumenregel > 5) verletzen. Daher recodieren wir zunächst die ziel_1-Variable.
8.2 Variablen recodieren
Wir haben schon gelernt, wie wir mit mutate() und if_else() Dummy-Variablen mit zwei Ausprägungen erstellen. Dies wäre für die ziel_1-Variable sehr streng, denn grob können wir deren Ausprägungen (siehe hierzu die Dokumentation zum Datensatz) in Online-Handlungen (1-5), Offline-Handlungen (6-7) und Gewaltaufrufe (8) unterteilen, also in drei Ausprägungen. Eine generalisierte Version von if_else() bietet case_when(). Sie eignet sich vor allem, um Variablen mit mehr als zwei Ausprägungen zu erstellen. Hier fassen wir die Ausprägungen der ziel_1-Variable so zusammen, dass alle Online-Handlungen (1), alle Offline-Handlungen (2) und Gewaltaufrufe (3) in einer neuen Variable zusammengefasst werden.
Für case_when() ist eine etwas schwierige Syntax erforderlich, in der Form Bedingung ~ neue Ausprägung, wobei beliebig viele dieser aufeinander folgen können. Es hilft, diese Bedingungen optisch zeilenweise zu trennen, um leichter zu erkennen, was passiert. Die Bedingungen werden nacheinander abgearbeitet, d.h. jeder Fall bekommt immer die erste Bedingung zugewiesen, die zutrifft. Am Ende werden mit TRUE ~ NA alle Fälle auf fehlende Werte gesetzt, für die keine der vorherigen Bedingungen zutrifft. In unserem Fall wären das die Werte -1 und -9, von denen wir ja auch wollen, dass sie im Folgenden als NA behandelt werden.
tg <- tg |>
mutate(ziel_1_recodiert = case_when(
ziel_1 == 1 ~ 1,
ziel_1 == 2 ~ 1,
ziel_1 == 3 ~ 1,
ziel_1 == 4 ~ 1,
ziel_1 == 5 ~ 1,
ziel_1 == 6 ~ 2,
ziel_1 == 7 ~ 2,
ziel_1 == 8 ~ 3,
TRUE ~ NA
))Nun haben wir schon bei der original ziel_1-Variable festgestellt, dass die Zahlen uns wenig sagen und wir immer parallel in die Dokumentation schauen müssen, um zu verstehen, was die Zahlenwerte bedeuten. Alternativ können wir textliche Ausprägungen verwenden, was das schnelle Lesen der Tabelle vereinfacht. Dies ist allerdings nur dann möglich, wenn es sich nicht um eine metrische Variable handelt, mit der wir noch Mittelwerte o.ä. berechnen wollen. In diesem Fall ist es kein Problem, wir benötigen diese Variable nur als Faktor, also z.B. um Gruppen zu vergleichen.
tg <- tg |>
mutate(ziel_1_recodiert = case_when(
ziel_1 == 1 ~ "Online-Handlungen",
ziel_1 == 2 ~ "Online-Handlungen",
ziel_1 == 3 ~ "Online-Handlungen",
ziel_1 == 4 ~ "Online-Handlungen",
ziel_1 == 5 ~ "Online-Handlungen",
ziel_1 == 6 ~ "Offline-Handlungen",
ziel_1 == 7 ~ "Offline-Handlungen",
ziel_1 == 8 ~ "Gewaltaufrufe",
TRUE ~ NA
))Im obigen Beispiel müssen wir für jede Ausprägung der ziel_1-Variablen eine Zeile anlegen und wiederholt denselben neuen Wert vergeben. Das können wir vereinfachen, indem wir den %in%-Operator verwenden. So geben wir an, welche Ausprägungen der alten Variablen dieselbe Ausprägung in der neuen Variablen bekommen sollen - in unserem Beispiel sind das etwa 1, 2, 3, 4 und 5. x %in% y prüft, ob ein Wert x in einer Menge y vorkommt, und gibt dann TRUE zurück. In diesem Fall weisen wir dann den jeweiligen Wert für die neue Variable zu. Das Beispiel oben können wir also etwas vereinfachen.
tg |>
mutate(ziel_1_recodiert = case_when(
ziel_1 %in% c(1, 2, 3, 4, 5) ~ "Online-Handlungen",
ziel_1 %in% c(6, 7) ~ "Offline-Handlungen",
ziel_1 == 8 ~ "Gewaltaufrufe",
TRUE ~ NA
))Der %in% Operator ist auch beim if_else()- oder filter()-Befehl oft nützlich.
8.3 Kreuztabelle
Nun können wir die Variable ziel_1_recodiert in Abhängigkeit von der ideologischen Ausrichtung des Telegram-Kanals analysieren. Wir fragen also, ob sich die Häufigkeiten der Zielstellung je nach Kanalart unterscheiden. Dies geht am besten mit einer Kreuztabelle. Zunächst versuchen wir einfach, zwei Variablen in count() auszuzählen:
tg |>
count(ideologie, ziel_1_recodiert)# A tibble: 12 × 3
ideologie ziel_1_recodiert n
<chr> <chr> <int>
1 Querdenken Gewaltaufrufe 6
2 Querdenken Offline-Handlungen 432
3 Querdenken Online-Handlungen 746
4 Querdenken <NA> 1446
5 Rechte Gewaltaufrufe 29
# ℹ 7 more rowsDies klappt, aber die Häufigkeiten sind im sog. Langformat angeordet. Wir wollen aber eine klassische Kreuztabelle, in der die unabhängige Variable (uV) ideologie in den Spalten und die abhängige Variable (aV) ziel_1_recodiert in den Zeilen ist. Das geht mit der Funktion table(). Wir wählen zunächst die Variablen (erst aV, dann uV) mit select() und erstellen dann die Kreuztabelle.
tg |>
select(ziel_1_recodiert, ideologie) |>
table() ideologie
ziel_1_recodiert Querdenken Rechte Verschwörung
Gewaltaufrufe 6 29 4
Offline-Handlungen 432 458 91
Online-Handlungen 746 2405 900Die Tabelle enthält nun die absoluten Häufigkeiten für jede Zelle. Dies lässt nur bedingt auf Unterschiede in den kommunikativen Strategien schließen, da sich die Gesamtzahl der Nachrichten zwischen den Ideologien stark unterscheidet. Wir können diese Tabelle aber als Grundlage für weitere Berechnungen, v.a. den Chi-Quadrat-Test, der auf den absoluten Häufigkeiten beruht, als eigenes Objekt ideo_table speichern.
Über den Befehl prop.table() können wir die Werte zur besseren Vergleichbarkeit prozentuieren. Wichtig ist, dass wir spaltenweise prozentuieren. Dies erreichen wir über den Zusatz prop.table(margin = 2) wobei die 2 spaltenweise Prozentuierung ergibt, die 1 eine zeilenweise Prozentuierung. Über den Zusatz round(digits = 2) können wir die Zahl der Nachkommastellen reduzieren. In unserem Fall reichen uns zwei Nachkommastellen.
ideo_table <- tg |>
select(ziel_1_recodiert, ideologie) |>
table()
ideo_table |>
prop.table(margin = 2) |>
round(digits = 2) ideologie
ziel_1_recodiert Querdenken Rechte Verschwörung
Gewaltaufrufe 0.01 0.01 0.00
Offline-Handlungen 0.36 0.16 0.09
Online-Handlungen 0.63 0.83 0.90Wir sehen, dass in den Querdenken-Kanälen Aufrufe zu Offline-Aktivitäten wie Demonstrationen deutlich häufiger sind als in den anderen beiden Kanalarten.
Üblicherweise präsentieren wir bei Kreuztabellen auch eine Gesamtspalte, die wir mit addmargins() in der Pipe hinzufügen können. Außerdem ist es übersichtlicher, gleich ganze gerundete Prozentwerte anzugeben. Dazu können wir die finale Ergebnistabelle einfach mit 100 multiplizieren und dann runden.
ideo_final <- ideo_table |>
addmargins(margin = 2) |>
prop.table(margin = 2)
round(ideo_final * 100, digits = 0) ideologie
ziel_1_recodiert Querdenken Rechte Verschwörung Sum
Gewaltaufrufe 1 1 0 1
Offline-Handlungen 36 16 9 19
Online-Handlungen 63 83 90 80Diese aufgeräumte Kreuztabelle wäre das erste Ergebnis unserer Analyse, die uns hilft, konkrete Gruppenunterschiede zu beschreiben.
8.4 Chi-Quadrat-Test
Die Kreuztabelle gibt die Verteilung der Kategorien in der Stichprobe wieder. Wir wollen nun prüfen, ob diese signifikant von einer Gleichverteilung über die Telegram-Kanäle abweicht. Dazu dient der Chi-Quadrat-Test auf Unabhängigkeit, der prüft ob die Verteilung von \(y\) unabhängig von der Gruppenvariable \(x\) ist.
- Nullhypothese H0
-
Die Verteilung der Variable
ziel_1_recodiertist unabhängig von der ideologischen Ausrichtung des Kanals.
Auf Basis der Häufigkeitstabelle ideo_table (ACHTUNG: Hierfür brauchen wir diese Version, nicht die oben erstellte ideo_final, da der Chi-Quadrat-Test auf den absoluten Häufigkeiten beruht) kann über die Funktion chisq.test() ganz leicht der Chi-Quadrat-Test durchgeführt werden.
ideo_table |>
chisq.test()
Pearson's Chi-squared test
data: ideo_table
X-squared = 316.61, df = 4, p-value < 2.2e-16Die Funktion liefert den Chi-Quadrat-Wert sowie die Freiheitsgrade und den p-Wert zurück.
In unserem Fall deutet der Chi-Quadrat-Test auf einen signifikanten Unterschied in der Verwendung verschiedener Appell-Formen zwischen den Ideologien hin. Sprich: Wären in der Grundgesamtheit in allen Arten von Kanälen die Appell-Formen gleichverteilt, wäre die Verteilung der Appelle unserer Stichprobe (oder eine noch stärkere Ungleichheit) extrem unwahrscheinlich (p < .001; der oben angezeigte p-Wert 2.2e-16 entspricht der Zahl 0.00000000000000022, denn e-16 bedeutet, dass erst ab der 16. Stelle nach dem Komma die erste Zahl kommt). Wir lehnen die Nullhypothese daher ab.
Um die Stärke des Zusammenhangs zu überprüfen, verwenden wir die report_table()-Funktion, die zusätzlich noch Cramer’s V als Effektstärkemaß berechnet.
ideo_table |>
chisq.test() |>
report_table()Pearson's Chi-squared test
Chi2(4) | p | Cramer's V (adj.) | Cramers_v_adjusted CI
-------------------------------------------------------------
316.61 | < .001 | 0.18 | [0.16, 1.00]Die Ergebnisse deuten auf einen eher schwachen Zusammenhang zwischen Ideologie und Appell-Formen hin.
Wenn wir die Stärke von Zusammenhängen bewerten, orientieren wir uns oft an Cohen (1988):
.10: Kleiner Effekt
.30: Mittlerer Effekt
.50: Großer Effekt
Betrachten wir die Kreuztabelle und den Chi-Quadrat-Test gemeinsam, kommen wir zu folgendem Ergebnis:
Insgesamt finden sich über alle Kanalarten hinweg sehr selten Gewaltaufrufe, am häufigsten wird zu Online-Handlungen aufgerufen. Dabei gibt es signifikante Unterschiede zwischen den verschiedenen Kanalarten (Chi²(4) = 316.61, p < .001). Es zeigt sich, dass Querdenker-Kanäle häufiger als die anderen Kanäle auch zu Offline-Handlungen aufrufen, gefolgt von rechten Kanälen. Der Zusammenhang ist eher schwach ausgeprägt (Cramer’s V = 0.18).
8.5 Visualisierung
Für die Visualisierung von Kreuztabellen werden fast immer gestapelte oder gruppierte Balkendiagramme verwendet. Hierfür müssen wir zunächst die für uns relevanten relativen Häufigkeiten als Tibble im Langformat berechnen, weil ggplot nicht direkt mit table Objekten arbeiten kann. Da sich unsere Darstellung nur auf Aufrufe beschränkt, filtern wir zunächst alle Fälle ohne Aufruf in ziel_1 heraus. Anschließend zählen wir die Häufigkeiten nach Ideologie und Aufrufstypen. Da wir als unabhängige Variable ideologie verwenden, berechnen wir nun diese Spaltenprozente durch die Kombination von group_by() und mutate(). Der entstehende Tibble ist Grundlage für unsere Grafik.
ideo_tab_long <- tg |>
filter(!is.na(ziel_1_recodiert)) |>
count(ideologie, ziel_1_recodiert) |>
group_by(ideologie) |>
mutate(percent = n / sum(n) * 100)
ideo_tab_long# A tibble: 9 × 4
# Groups: ideologie [3]
ideologie ziel_1_recodiert n percent
<chr> <chr> <int> <dbl>
1 Querdenken Gewaltaufrufe 6 0.507
2 Querdenken Offline-Handlungen 432 36.5
3 Querdenken Online-Handlungen 746 63.0
4 Rechte Gewaltaufrufe 29 1.00
5 Rechte Offline-Handlungen 458 15.8
# ℹ 4 more rowsWir definieren ein Balkendiagramm mit der Ideologie auf der x-Achse, den gültigen Prozentwerten auf der y-Achse, und füllen die Balken je nach Art des Aufrufs. Damit erhalten wir ein gestapeltes Balkendiagramm.
ideo_tab_long |>
ggplot(aes(x = ideologie, y = percent, fill = ziel_1_recodiert)) +
geom_col() +
labs(x = "Art des Telegram-Kanals", y = "Häufigkeit (%)", fill = "Art der Aufrufe")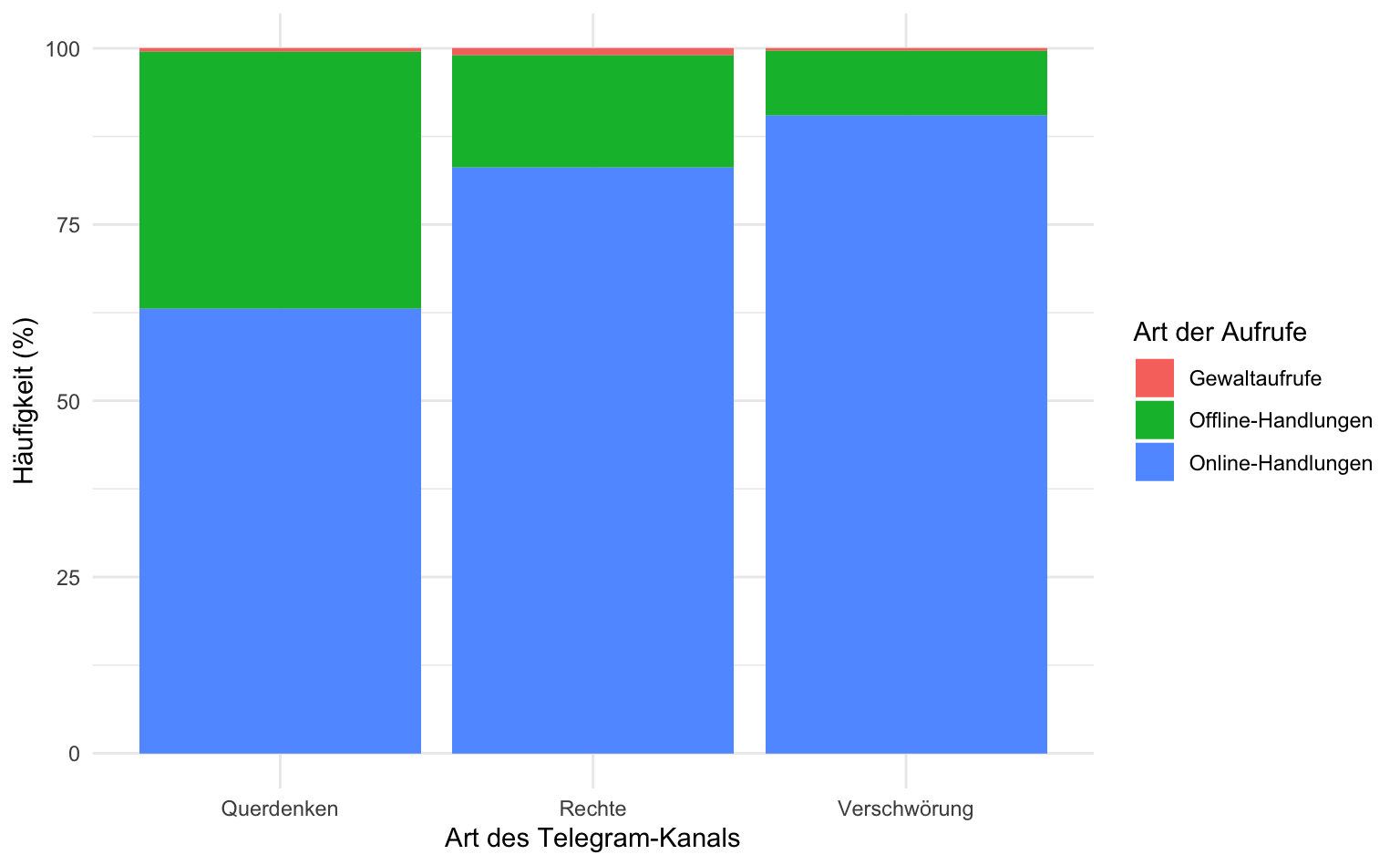
Wenn das gestapelte Balkendiagramm zu unübersichtlich ist, können wir es mit eine kleinen Änderung (position = position_dodge()) in ein gruppiertes Balkendiagramm verwandeln.
ideo_tab_long |>
ggplot(aes(x = ideologie, y = percent, fill = ziel_1_recodiert)) +
geom_col(position = position_dodge()) +
labs(x = "Art des Telegram-Kanals", y = "Häufigkeit (%)", fill = "Art der Aufrufe")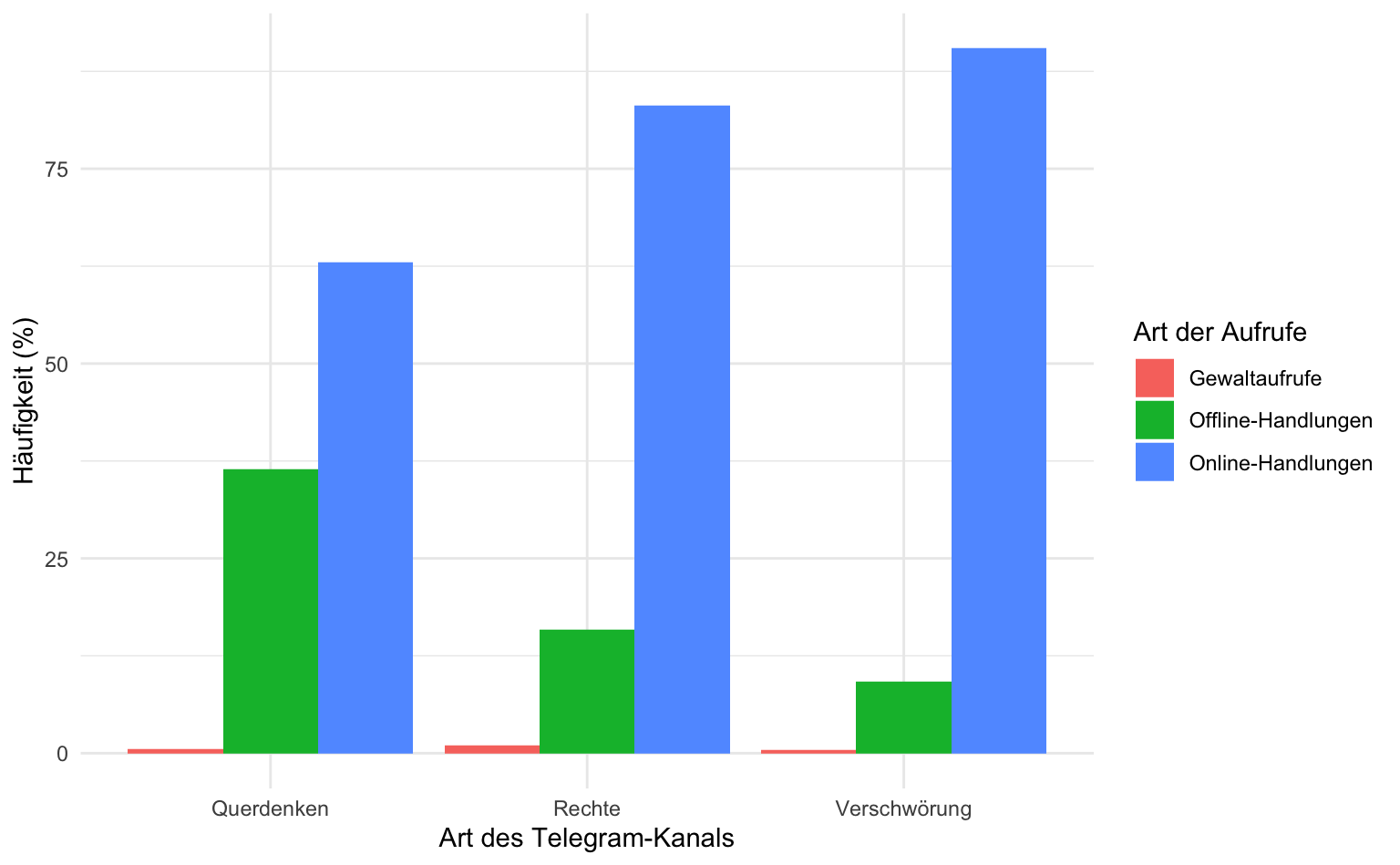
8.6 Glossar
| Funktion | Definition |
|---|---|
| addmargins() | Hinzufügen der Randhäufigkeiten |
| chisq.test() | Berechnen des Chi2-Tests |
| mutate() | Verändern oder Erstellen einer oder mehrerer Variablen in einem Dataframe/Tibble |
| prop.table() | Konvertierung einer Tabelle von absoluten zu relativen Häufigkeiten |
| report_table() | Erstellen einer Ergebnis-Tabelle aus einem statistischen Modell |
| table() | Erstellen von uni- und bivariaten Tabellen mit absoluten Häufigkeiten |
8.7 Hausaufgabe
Für die Hausaufgabe analysieren wir den Datensatz gewohnheiten.xlsx.
- Unterscheiden sich Männer und Frauen darin, ob sie Zugang zu einem Tablet haben? Wenn ja, wie stark?
- Prüfen Sie die Hypothese, dass höher gebildete Befragte eher Zugang zu einer Tageszeitung haben.
Für alle Aufgaben gilt:
- Geben Sie als Kommentar (mit # beginnend) an, welche Frage Sie bearbeiten, darunter folgt der zugehörige Code.
- Betrachten Sie zunächst die Variablen univariat.
- Führen Sie dann die bivariate(n) Analyse(n) durch und beschreiben und interpretieren deren Ergebnisse.
- Die Antwortsätze folgen darunter, ebenfalls als Kommentar (mit # beginnend).