library(report)
library(tidyverse)
theme_set(theme_minimal())
vb <- readxl::read_excel("data/victim_blaming.xlsx")11 Korrelation und Regression
Wir laden das report- und das tidyverse-Paket und öffnen den Datensatz des Victim Blaming Experiments.
11.1 Korrelation
Wir stellen uns die Frage, ob es einen linearen Zusammenhang zwischen Sympathie (v_5k) und Mitleid mit dem Opfer (v_11) gibt. Beide Variablen sind metrisch skaliert. Deshalb bietet sich eine Korrelationsanalyse an, und zwar genauer die Produkt-Moment-Korrelationskoeffizient r nach Pearson.
Unsere Hypothese ist, dass beide Variablen in einem positiven Zusammenhang stehen sollten (mehr Sympathie, mehr Mitleid).
- Nullhypothese H0
- Sympathie und Mitleid sind voneinander unabhängig.
Vor der bivariaten Analyse betrachten wir die Stichprobenkennwerte der beiden Variablen zunächst wieder univariat, mit summarise().
vb |>
summarise(
m_symp = mean(v_5k, na.rm = TRUE),
sd_symp = sd(v_5k, na.rm = TRUE),
m_mitleid = mean(v_11, na.rm = TRUE),
sd_mitleid = sd(v_11, na.rm = TRUE)
)# A tibble: 1 × 4
m_symp sd_symp m_mitleid sd_mitleid
<dbl> <dbl> <dbl> <dbl>
1 3.19 1.09 4.02 0.856Beide Variablen variieren substanziell, so dass wir auch eine mögliche Kovarianz und damit Korrelation berechnen können. Diese Berechnung samt Signifikanztest übernimmt die Funktion cor.test(). Da es bei Korrelationsanalysen keine Unterscheidung von unabhängiger und abhängiger Variable gibt, sondern einfach zwei Variablen x1 und x2, sieht die Formel in der Funktion etwas anders aus als bei t-Test und Varianzanalyse: cor.test(~ x1 + x2, data = Datenframe)
cor.test(~ v_5k + v_11, data = vb)
Pearson's product-moment correlation
data: v_5k and v_11
t = -5.2887, df = 584, p-value = 1.744e-07
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.2897674 -0.1351338
sample estimates:
cor
-0.2137895 Wir sehen, dass die Korrelation in der Stichprobe r = -.21 ist. Das ist angesichts unserer Hypothese ziemlich überraschend. Wir schauen noch einmal in der Variablenliste des Datensatzes nach und stellen fest, dass Sympathie mit 1 = sympathisch bis 5 = unsympathisch gemessen wurde. Ein höherer Wert steht also für weniger Sympathie, und damit ergibt die negative Korrelation inhaltlich wieder Sinn.
In der explorativen Forschungspraxis werden oft mehrere Variablen miteinander korreliert und diese vielen Korrelationen dann in Form einer sog. Korrelationsmatrix dargestellt. Diese lässt sich mit dem cor()-Befehl erzeugen. Wichtig ist dabei zu entscheiden, ob die fehlenden Werte paarweise oder listenweise ausgeschlossen werden sollen. Bei ersterem basiert jede Korrelation potentiell auf einer anderen Stichprobe - nämlich auf den Fällen, die für die beiden im jeweiligen Fall korrelierten Variablen einen gültigen Wert haben. Bei letzterem basieren alle Korrelationen auf derselben Stichprobe - nämlich auf den Fällen, die in allen Variablen, die in der Korrelationsmatix berücksichtigt werden, einen gültigen Wert haben. Damit kann diese Stichprobe deutlich kleiner ausfallen. Meist ist es sinnvoll, mit paarweisem Ausschluss zu arbeiten.
Hier explorieren wir die Zusammenhänge zwischen allen Variablen des v_5-Blocks mit paarweisem Ausschluss. Das Runden auf zwei Nachkommastellen macht die Matrix etwas lesbarer.
vb |>
select(starts_with("v_5")) |>
cor(use = "pairwise") |> # alternativ: complete
round(digits = 2) v_5a v_5b v_5c v_5d v_5e v_5f v_5g v_5h v_5i v_5j v_5k
v_5a 1.00 0.58 -0.61 0.20 -0.23 -0.21 -0.15 0.17 -0.20 -0.07 0.05
v_5b 0.58 1.00 -0.58 0.21 -0.23 -0.21 -0.18 0.16 -0.19 -0.10 0.01
v_5c -0.61 -0.58 1.00 -0.28 0.28 0.30 0.19 -0.18 0.26 0.13 -0.04
v_5d 0.20 0.21 -0.28 1.00 -0.56 -0.68 -0.55 0.61 -0.73 0.19 0.49
v_5e -0.23 -0.23 0.28 -0.56 1.00 0.47 0.65 -0.42 0.57 0.01 -0.25
v_5f -0.21 -0.21 0.30 -0.68 0.47 1.00 0.45 -0.57 0.73 -0.18 -0.42
v_5g -0.15 -0.18 0.19 -0.55 0.65 0.45 1.00 -0.41 0.52 0.03 -0.22
v_5h 0.17 0.16 -0.18 0.61 -0.42 -0.57 -0.41 1.00 -0.57 0.30 0.46
v_5i -0.20 -0.19 0.26 -0.73 0.57 0.73 0.52 -0.57 1.00 -0.13 -0.44
v_5j -0.07 -0.10 0.13 0.19 0.01 -0.18 0.03 0.30 -0.13 1.00 0.49
v_5k 0.05 0.01 -0.04 0.49 -0.25 -0.42 -0.22 0.46 -0.44 0.49 1.00Da wir (und die Leser:innen) jetzt immer daran denken müssten, dass die Variable eigentlich falsch herum codiert ist - es ist nicht intuitiv, dass eine höhere Sympathie einen niedrigeren Skalenwert hat -, bietet es sich an, sie gleich richtig herum zu codieren.
vb <- vb |>
mutate(symp = 6 - v_5k)Jetzt führen wir den Korrelationstest mit der neuen Variable durch, es sollte sich nichts als das Vorzeichen ändern.
cor.test(~ symp + v_11, data = vb)
Pearson's product-moment correlation
data: symp and v_11
t = 5.2887, df = 584, p-value = 1.744e-07
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.1351338 0.2897674
sample estimates:
cor
0.2137895 Die Funktion liefert neben dem Korrelationskoeffizienten ganz unten auch noch die Teststatistiken samt Freiheitsgraden und p-Wert sowie das Konfidenzintervall für r. Auch hier können wir mit report_table() eine übersichtliche Tabelle bekommen.
cor.test(~ symp + v_11, data = vb) |>
report_table()Pearson's product-moment correlation
Parameter1 | Parameter2 | r | 95% CI | t(584) | p
---------------------------------------------------------------
symp | v_11 | 0.21 | [0.14, 0.29] | 5.29 | < .001
Alternative hypothesis: two.sidedWir erkennen am p-Wert, dass es sehr unwahrscheinlich wäre, unseren Korrelationskoeffizienten oder einen noch höheren zu erhalten, wenn in der Grundgesamtheit kein Zusammenhang zwischen den Variablen bestünde. Wir lehnen die Nullhypothese daher ab, der Zusammenhang ist statistisch signifikant. Das erkennen wir auch daran, dass der 95%-CI nicht die Null enthält. Der Zusammenhang ist substantiell aber eher schwach bis mittel ausgeprägt (siehe die Faustregeln nach Cohen (1988) zur Interpretation der Effektstärke).
Es besteht ein schwacher bis mittlerer signifikanter positiver Zusammenhang zwischen Sympathie und Mitleid mit dem Opfer (r = .21, p < .001): Je sympathischer das Opfer wahrgenommen wird, desto größer auch das Mitleid.
Die cor.test()-Funktion beinhaltet ein method-Argument, mit dem auch Rangkorrelationen statt Pearson’s r geschätzt werden. Dies machen wir dann, wenn mindestens eine der beiden Variablen ordinales Datenniveau hat. Dafür setzen wir das Argument auf spearman oder kendall. Die statistischen Tests unterscheiden sich natürlich, aber Output und Interpretation sind fast identisch.
cor.test(~ symp + v_11, data = vb, method = "spearman")
Spearman's rank correlation rho
data: symp and v_11
S = 26426036, p-value = 2.2e-07
alternative hypothesis: true rho is not equal to 0
sample estimates:
rho
0.2120626 11.2 Bivariate Regression
Interessieren wir uns für den Zusammenhang zwischen zwei metrischen Variablen, können wir anstelle einer Korrelationsanalyse auch eine lineare Regression schätzen. Dafür müssen wir uns entscheiden, was unabhängige und was abhängige Variablen sind. Wir gehen hier davon aus, dass die Sympathie zumindest zeitlich vor dem Mitleid da war, d.h. wir schätzen mit der Regressionsanalyse den Einfluss der Sympathie auf das Mitleid.
- Nullhypothese H0
- Sympathie hat keinen Einfluss auf Mitleid.
Lineare Regressionen können in R mit der Funktion lm() durchgeführt werden, die Formelsyntax ist dabei identisch mit t.test() und aov() bei den Mittelwertvergleichen: lm(abhängige_variable ~ unabhängige_variable, data = Datenframe).
lm(v_11 ~ symp, data = vb)
Call:
lm(formula = v_11 ~ symp, data = vb)
Coefficients:
(Intercept) symp
3.5440 0.1679 Wir bekommen zunächst nur die beiden Regressionskoeffizienten für den Intercept (= Y-Achsenabschnitt) und Sympathie. Der vorausgesagte Mitleids-Score wäre 3.54, wenn die Sympathie-Variable den Wert 0 hätte. Da Sympathie aber von 1-5 skaliert ist, kann die Variable niemals den Wert 0 haben. Deshalb können wir den Intercept-Term hier nicht interpretieren. Dafür aber den Regressionskoeffizienten b für Sympathie: Steigt (bzw. sinkt) diese Variable um einen Skalenpunkt, steigt (bzw. sinkt) der vorausgesagte Wert für Mitleid um 0.16.
In den meisten Fällen interessieren wir uns nicht für die Interpretation des Intercepts. Wenn uns dieser aber wichtig ist, können wir dafür sorgen, dass er interpretierbar wird. Dazu müssen wir alle unabhängigen Variablen so codieren, dass die 0 als Wert möglich ist. Ein sehr üblicher Weg dies zu erreichen ist die sogenannte Zentrierung von Variablen. Im Fall von Symphatie würden wir den Mittelwert der Variablen berechnen und dann von den Sympathiewerten der einzelnen Teilnehmer:innen abziehen. So erhalten wir eine Sympathie-Variable, in der die 0 bedeutet, dass die Person das Opfer so sympathisch findet wie alle Teilnehmer:innen im Durchschnitt. Ein negativer Wert bedeutet entsprechend, dass die Person das Opfer unsympathischer findet als die anderen (im Schnitt), ein positiver Wert analog, dass sie das Opfer sympathischer findet.
vb <- vb |>
mutate(symp_c = symp - (mean(symp)), na.rm = TRUE)Rechnen wir die Regression dann mit dieser neuen Variablen, können wir den Intercept interpretieren: Er sagt uns, wie viel Mitleid das Opfer erfährt, wenn es als durchschnittlich sympathisch eingeschätzt wird. An b ändert sich nichts, alle anderen Parameter bleiben von dieser Transformation unbeeinflusst.
lm(v_11 ~ symp_c, data = vb)
Call:
lm(formula = v_11 ~ symp_c, data = vb)
Coefficients:
(Intercept) symp_c
4.0154 0.1679 Im obigen Output sehen wir die Stichprobenkennwerte, d.h. ob diese statistisch signifikant sind, können wir nicht ablesen. Daher nutzen wir wieder report_table().
lm(v_11 ~ symp, data = vb) |>
report_table()Parameter | Coefficient | 95% CI | t(584) | p | Std. Coef.
-----------------------------------------------------------------------
(Intercept) | 3.54 | [3.36, 3.73] | 37.07 | < .001 | -1.83e-16
symp | 0.17 | [0.11, 0.23] | 5.29 | < .001 | 0.21
| | | | |
AIC | | | | |
AICc | | | | |
BIC | | | | |
R2 | | | | |
R2 (adj.) | | | | |
Sigma | | | | |
Parameter | Std. Coef. 95% CI | Fit
-----------------------------------------
(Intercept) | [-0.08, 0.08] |
symp | [ 0.13, 0.29] |
| |
AIC | | 1458.64
AICc | | 1458.68
BIC | | 1471.76
R2 | | 0.05
R2 (adj.) | | 0.04
Sigma | | 0.84Wir erkennen am 95%-CI, das nicht die Null enthält, oder am p-Wert (p < .001), dass Sympathie das Mitleid statistisch signifikant vorhersagt. Der standardisierte Regressionskoeffizient \(\beta\) ist im bivariaten Fall identisch mit dem Korrelationskoeffizienten r = .21. Auch hier können wir - basierend auf Cohen (1988) - also von einem schwachen bis mittleren Effekt sprechen. Das R-Quadrat ist \(R^2\) = .04 (wir lesen immer das korrigierte R² ab, also R²(adj.)), d.h. unser Regressionsmodell kann 4% der Varianz in der Variable Mitleid vorhersagen.
Je sympathischer das Opfer eingeschätzt wird, desto mehr Mitleid haben die Teilnehmer:innen mit dem Opfer (\(\beta\) = .21, p < .001). Insgesamt können 4% der Varianz in der Variable Mitleid vorhergesagt werden (R² = .04).
11.3 Multiple Regression
Mit der lm()-Funktion können wir auch multiple Regressionen schätzen, bei denen es mehr als eine unabhängige Variable gibt. Die Syntax ist identisch, es werden einfach die Variablen mit + verbunden. Hier schauen wir, ob zusätzlich auch die wahrgenommene Schwere des Vorfalls v_6 das Mitleid vorhersagt. Wir erwarten, dass je schwerer der Vorfall wahrgenommen wird, desto mehr Mitleid sollten die Teilnehmer:innen mit der Protagonistin haben, selbst wenn wir die Sympathie konstant halten.
lm(v_11 ~ symp + v_6, data = vb) |>
report_table()Parameter | Coefficient | 95% CI | t(583) | p | Std. Coef.
-----------------------------------------------------------------------
(Intercept) | 0.78 | [0.18, 1.39] | 2.55 | 0.011 | -3.69e-16
symp | 0.14 | [0.08, 0.20] | 4.73 | < .001 | 0.18
v 6 | 0.59 | [0.47, 0.72] | 9.38 | < .001 | 0.36
| | | | |
AIC | | | | |
AICc | | | | |
BIC | | | | |
R2 | | | | |
R2 (adj.) | | | | |
Sigma | | | | |
Parameter | Std. Coef. 95% CI | Fit
-----------------------------------------
(Intercept) | [-0.07, 0.07] |
symp | [ 0.10, 0.25] |
v 6 | [ 0.28, 0.43] |
| |
AIC | | 1378.30
AICc | | 1378.36
BIC | | 1395.79
R2 | | 0.17
R2 (adj.) | | 0.17
Sigma | | 0.78Wir sehen, dass dies der Fall ist. Mit jedem Skalenpunkt mehr wahrgenommener Schwere des Vorfalls steigt das Mitleid um 0.59 Skalenpunkte. Beim Vergleich der standardisierten Koeffizienten \(\beta\) fällt auf, dass dieser mittelstarke Effekt doppelt so stark ist wie der der Sympathie. Außerdem hat sich die Vorhersagequalität unseres Modells, gemessen am (adjustierten) R-Quadrat, deutlich auf .17 erhöht - beide Variablen zusammen erklären also fast 20% der Varianz der Mitleid-Variable.
Sowohl die Sympathie als auch die wahrgenommene Schwere des Vorfalls beeinflussen das Mitleid mit dem Opfer signifikant: Je schwerwiegender der Vorfall wahrgenommen wird (\(\beta\) = .36, p < .001) und je sympathischer das Opfer eingeschätzt wird (\(\beta\) = .18, p < .001), desto mehr Mitleid haben die Teilnehmer:innen mit dem Opfer. Dabei hat die Wahrnehmung der Schwere des Vorfalls einen deutlich stärkeren Einfluss auf das Mitleid als die Sympathie. Insgesamt können mit dem Modell 17% der Varianz in der Variable Mitleid vorhergesagt werden (R² = .17).
11.4 Visualisierung
Die klassische Darstellung für den untersuchten Zusammenhang zwischen Sympathie und Mitleid ist ein Streudiagramm, das mit geom_point() oder geom_jitter() erstellt werden kann. Alternativ oder zusätzlich können wir mit geom_smooth(method = "lm") die Regressionsgerade samt Konfidenzintervall darstellen - im Hintergrund wird dafür das gleiche Regressionsmodell geschätzt wie oben.
vb |>
ggplot(aes(x = v_11, y = symp)) +
geom_jitter() +
geom_smooth(method = "lm") +
labs(x = "Mitleid", y = "Sympathie")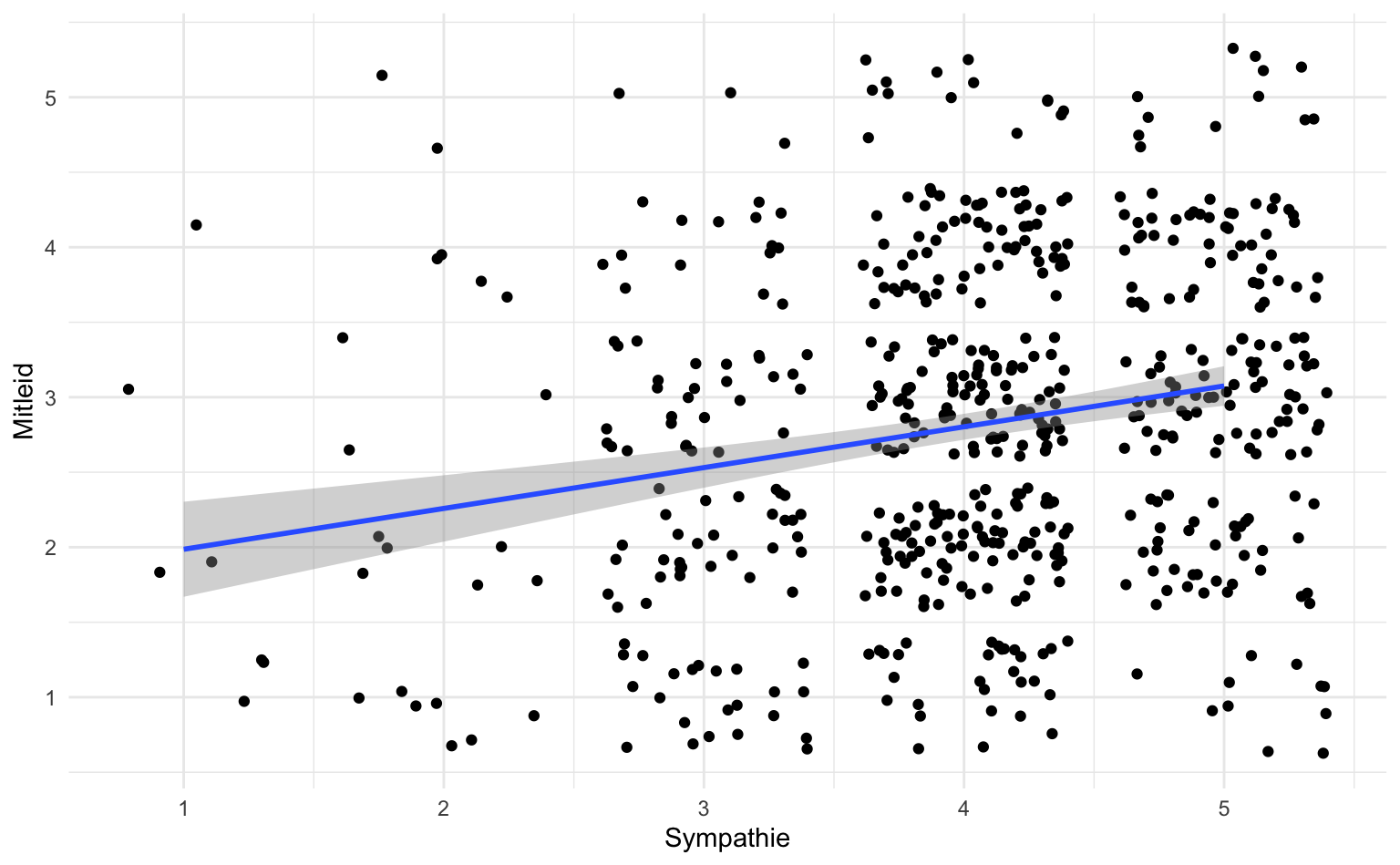
Die Darstellung für multiple Regressionsanalysen gestaltet sich etwas schwieriger, weshalb wir an dieser Stelle darauf verzichten.
11.5 Glossar
| Funktion | Definition |
|---|---|
| cor.test() | Berechnen von Korrelationskoeffizienten |
| lm() | Berechnen von Regressionsmodellen |
11.6 Hausaufgabe
Besteht ein Zusammenhang zwischen der Trait-Selbstkontrolle (
p_sc) und den drei Smartphone-Gewohnheitsdimensionen (smart_srhi_rep,smart_srhi_auto,smart_srhi_control)?Angelehnt an die Theory of Planned Behavior (z.B. Ajzen & Fishbein 2010) sollte sich die Smartphone-Nutzungsintensität durch die Einstellung (
s_einst), sozialen Normen (s_soz) und Kompetenzempfinden (s_komp) bzgl. der Smartphone-Nutzung erklären lassen.- Prüfen Sie den Einfluss von Einstellung, sozialen Normen, Kompetenzempfinden auf die Smartphone-Nutzungsintensität in einem Modell.
- Bitte beschreiben und interpretieren Sie, wie viel das Regressionsmodell erklären kann und beschreiben Sie welche Variablen einen Einfluss auf die Smartphone-Nutzungsintensität haben und welcher der stärkste ist.
Für alle Aufgaben gilt:
- Geben Sie als Kommentar (mit # beginnend) an, welche Frage Sie bearbeiten, darunter folgt der zugehörige Code.
- Betrachten Sie zunächst die Variablen univariat.
- Führen Sie dann die bivariate(n) Analyse(n) durch und beschreiben und interpretieren deren Ergebnisse.
- Die Antwortsätze folgen darunter, ebenfalls als Kommentar (mit # beginnend).