library(tidyverse)
theme_set(theme_minimal())
vb <- readxl::read_excel("data/victim_blaming.xlsx")
soziodemographie <- read_tsv("data/soziodemographie.tsv")7 Datenvisualisierung
Wir laden das tidyverse-Paket, setzen ein schöneres ggplot-Theme mit theme_set() (dies hat lediglich Auswirkungen auf die optische Darstellung der folgenden Grafiken) und öffnen den Datensatz des Victim Blaming-Experiments sowie den erfundenen Soziodemographie-Datensatz.
Im tidyverse werden alle Schritte der Datenvisualisierung durch das Paket ggplot2 umgesetzt. Das Paket verfolgt eine eigene Syntax, die sogenannte grammar of graphics, die allerdings in Grundzügen den Arbeitsschritten im tidyverse ähnelt (ein guter Überblick findet sich hier). Das Kernprinzip ist, verschiedene Datenelemente schrittweise übereinander zu legen. Die grundlegenden Elemente von ggplot() lassen sich in Daten, aesthetics und geometry einteilen. Die aesthetics bestimmen, welche Variablen zu welchen Dimensionen der Grafik, etwa Achsenabschnitten (x-Achse, y-Achse), Farben oder Formen zugewiesen werden, während die geometry die konkrete Darstellung (Punkte, Balken, Linien) bezeichnet. Ein Beispiel:
ggplot(data = df, aes(x = alter, y = einkommen)) +
geom_point() +
labs(x = "Alter", y = "Einkommen (in Euro/Monat)")Wir können diesen Code direkt lesen und uns vorstellen, wir die Grafik aussehen wird: Die Variable alter ist auf der x-Achse, die Einkommensvariable auf der y-Achse. Die Daten werden als Punkte dargestellt - ein klassischer Scatter-Plot. Die grammar of graphics ermöglicht uns also, rein verbal komplexe Diagramme zu beschreiben, und das ggplot2 Paket ermöglicht uns, diese Grafiken auch in R zu erstellen.
Die Übergabe des Datensatzes an die ggplot()-Funktion erfolgt wie zuvor mit der Pipe |>, während alle Befehle nach ggplot() mit dem Pluszeichen (+) verbunden werden. Warum? Wie bei einer Overhead-Folie werden verschiedene geom Schichten aufeinandergelegt, d.h. Elemente werden praktisch aufaddiert.
7.1 Balkendiagramm
Ein einfaches Balkendiagramm erstellen wir mit geom_col(). Wir nutzen dazu zunächst den erfundenen Soziodemographie-Datensatz, den wir im Kapitel R Grundlagen bereits verwendet haben.
soziodemographie# A tibble: 3 × 5
alter groesse name ist_verheiratet geschlecht
<dbl> <dbl> <chr> <lgl> <chr>
1 32 1.67 Maria Musterfrau FALSE Weiblich
2 54 1.82 Peter Mustermann TRUE Männlich
3 26 1.76 Kim Muster FALSE <NA> Nun wollen wir ein Balkendiagramm erstellen, bei dem auf der x-Achse die 3 Personen aufgelistet werden, während die Balkenhöhe (die y-Achse) deren Alter wiedergibt. Da es zur guten wissenschaftlichen Praxis gehört, Achsen sinnvoll zu beschriften, nutzen wir auch gleich labs(), mit dem sich Labels für alle Aspekte, die in aes() aufgeführt sind, festlegen lassen.
soziodemographie |>
ggplot(aes(x = name, y = alter)) +
labs(x = "Person", y = "Alter")
Wir erhalten ein leeres Koordinatensystem, aber die Achsen sind schon korrekt angeordnet und beschriftet. Erst wenn wir auch noch angeben, welche Art von grafischer Darstellung (geometry) wir wollen, zeichnet uns R auch die gewünschten Diagrammelemente. Hier nutzen wir geom_col() (eine Übersicht aller Möglichkeiten findet sich in diesem Cheat Sheet).
soziodemographie |>
ggplot(aes(x = name, y = alter)) +
labs(x = "Person", y = "Alter") +
geom_col()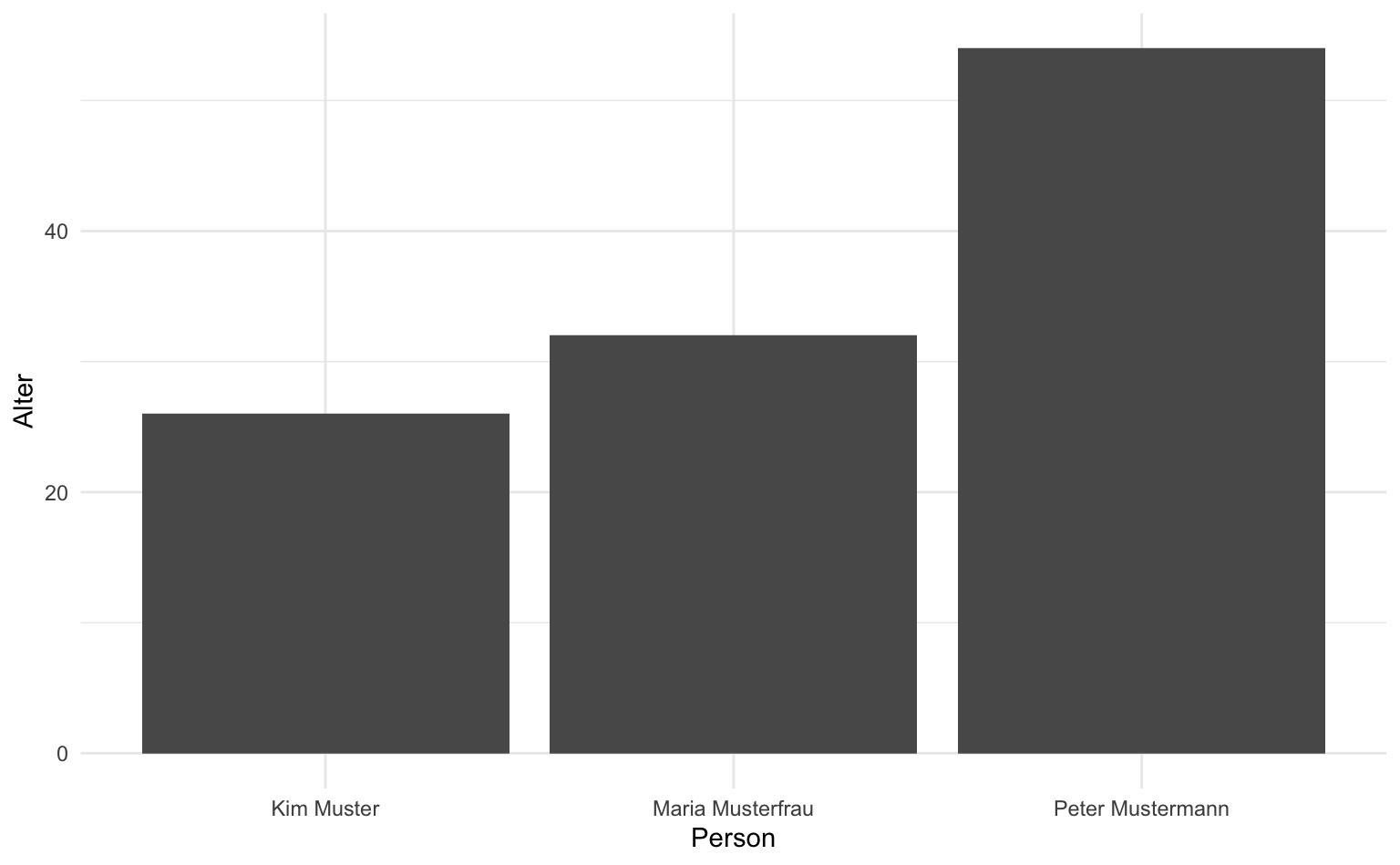
Wenn wir statt Balken lieber Punkte plotten wollen, können wir einfach das geom_col() durch geom_point() ersetzen, der Rest des Befehls ändert sich nicht. Alle geom-Funktionen können mit Hilfe zusätzlicher Parameter modifiziert werden. Dabei werden Farbe, Größe oder Form für alle Elemente festgelegt, d.h. sie variieren nicht in Abhängigkeit der Daten wie bei aesthetics. Hier machen wir alle Punkte etwas größer.
soziodemographie |>
ggplot(aes(x = name, y = alter)) +
labs(x = "Person", y = "Alter") +
geom_point(size = 5)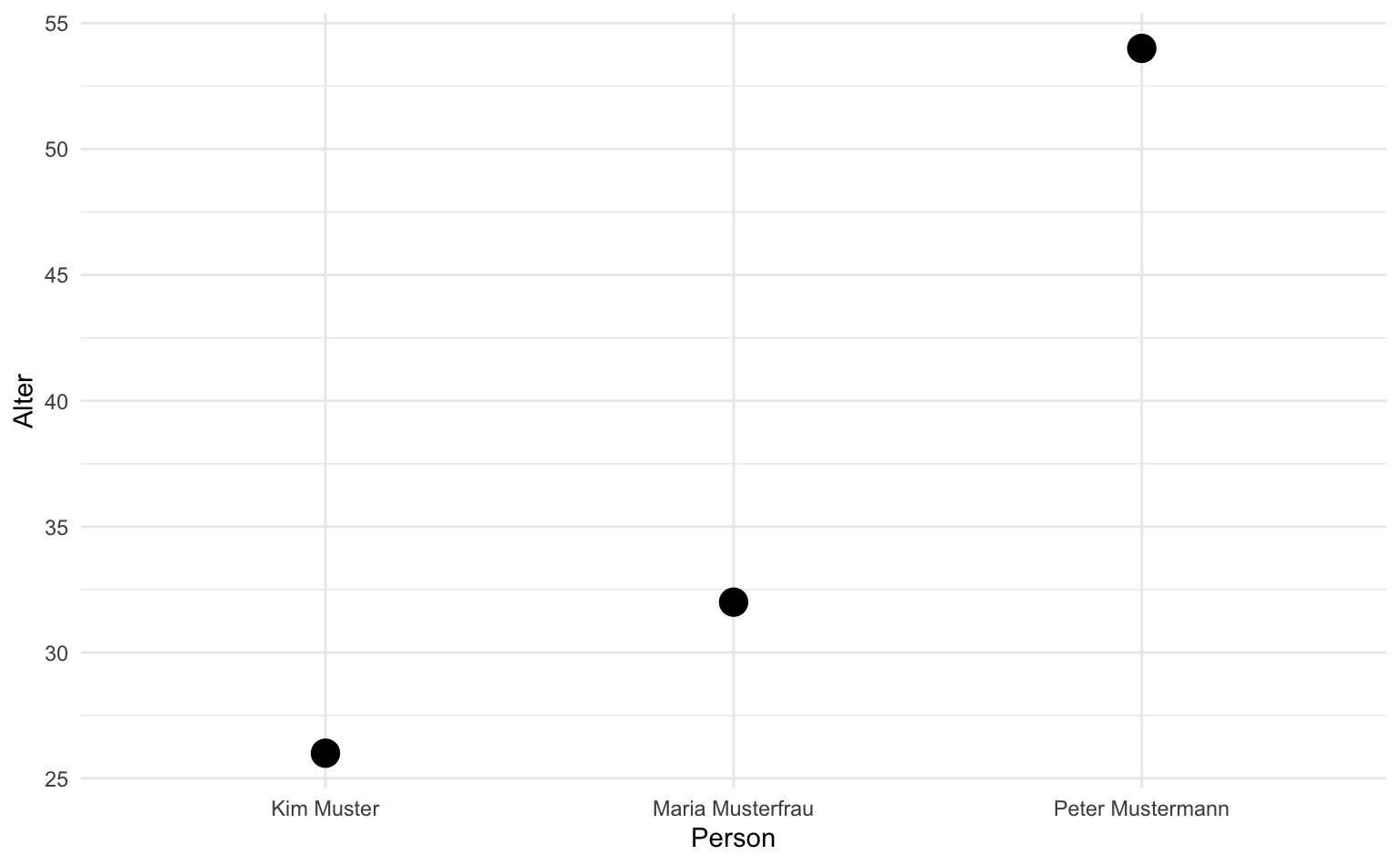
Weil die geom Schichten additiv sind, lassen sich auch Balken und Punkte plotten, indem wir sie einfach aufaddieren. Die Reihenfolge ist dabei manchmal relevant, da die letzte Schicht die vorige überdruckt:
soziodemographie |>
ggplot(aes(x = name, y = alter)) +
labs(x = "Person", y = "Alter") +
geom_col() +
geom_point(size = 5)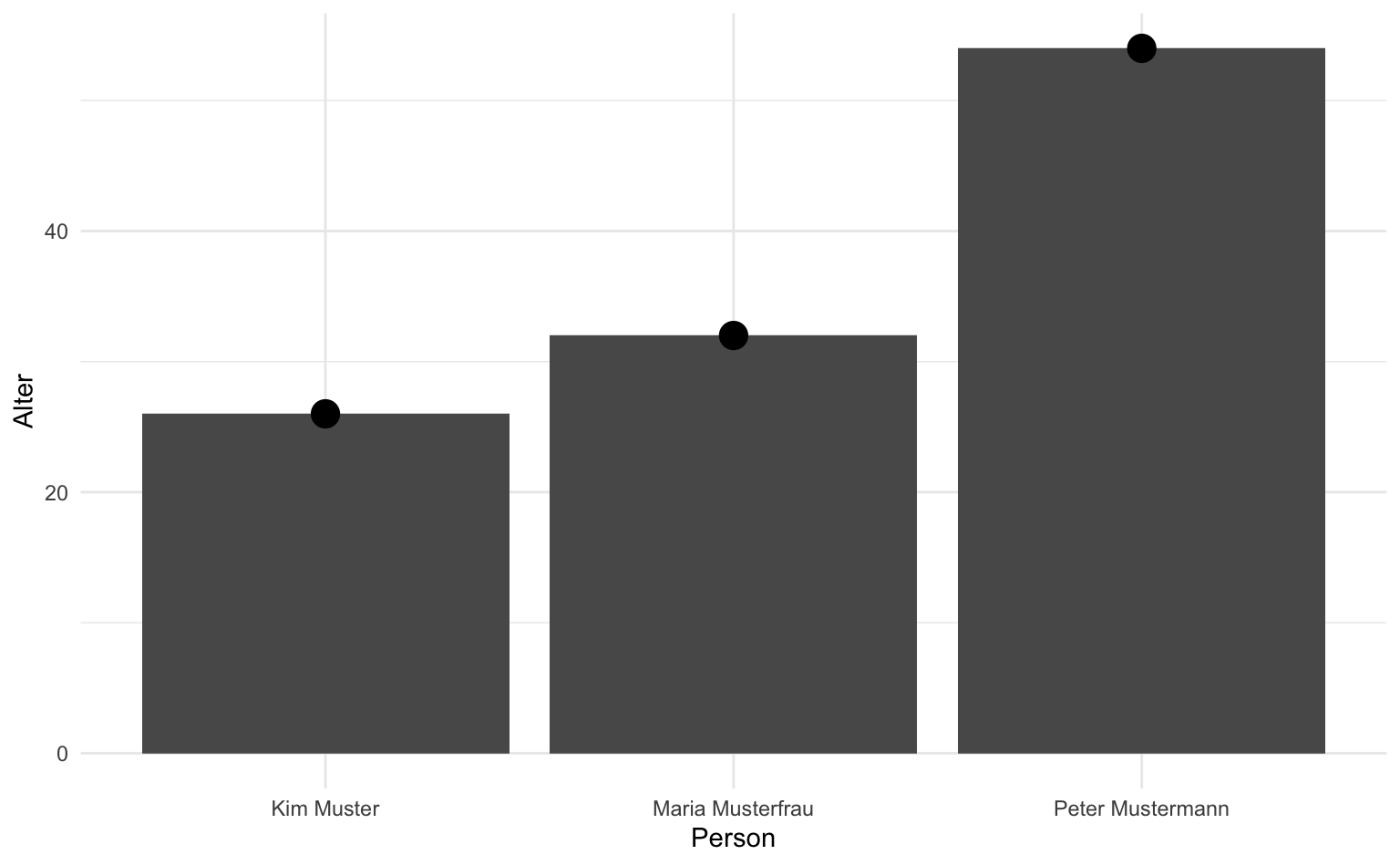
Wir können auch weitere Variablen aesthetics zuweisen, um mehr Informationen in der Grafik unterzubringen. Verwenden wir etwa fill mit der Variable ist_verheiratet, werden die Balken nach dem Familienstatus der Person eingefärbt. Wichtig: Wir legen nicht direkt fest, mit welcher Farbe sie eingefärbt werden, sondern sagen nur, dass sie in Abhängigkeit der Ausprägung von ist_verheiratet unterschiedlich dargestellt werden sollen.
soziodemographie |>
ggplot(aes(x = name, y = alter, fill = ist_verheiratet)) +
geom_col() +
labs(x = "Person", y = "Alter", fill = "Beziehungsstatus")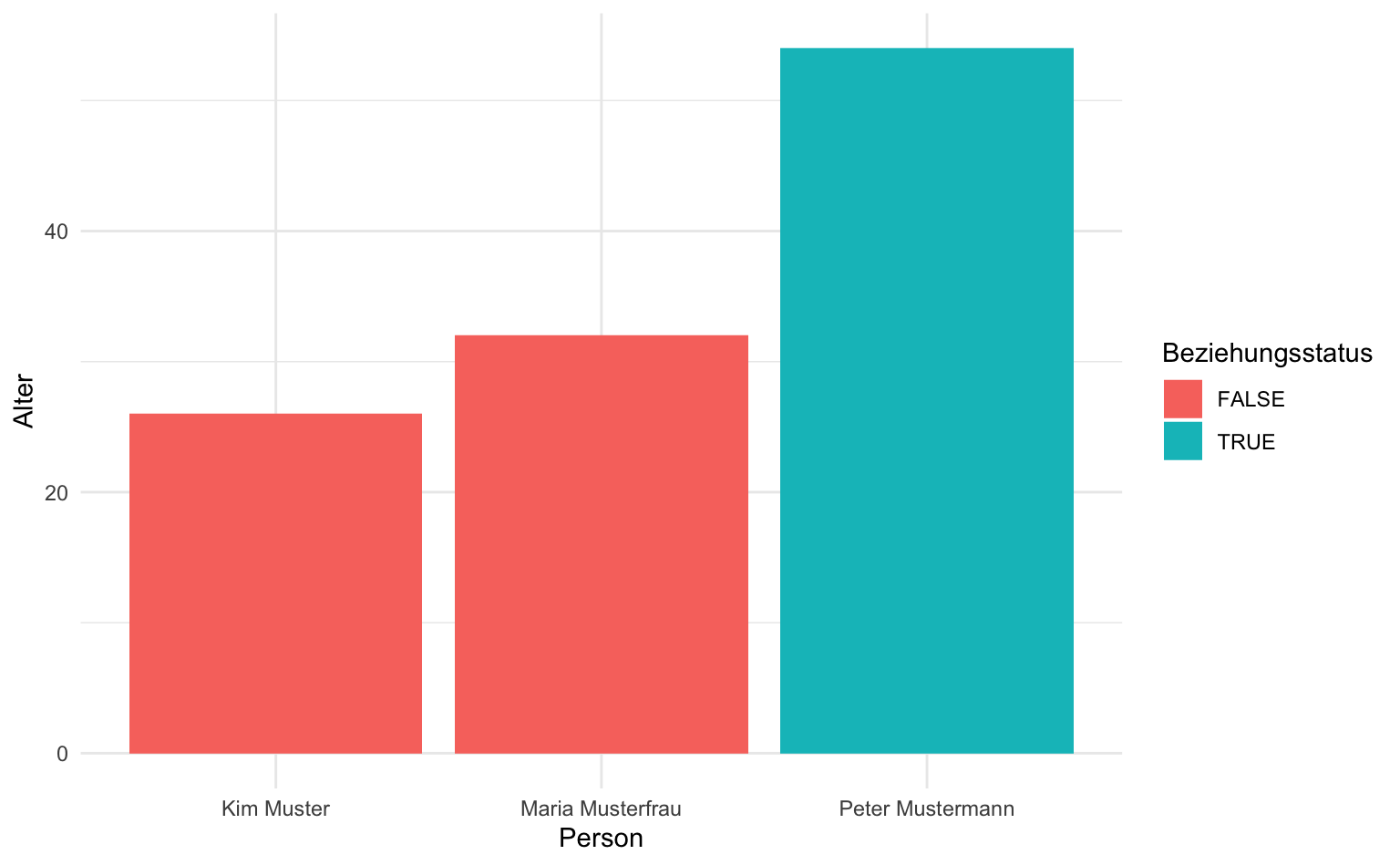
Wie können wir die Grafik noch verbessern? Die Ausprägungen TRUE und FALSE passen hier nicht sehr gut in der Legende, daher codieren wir sie am Anfang der Pipe nochmal mit if_else um. Außerdem wollen wir die Balken absteigend nach Alter statt alphabetisch ordnen. Hierfür können wir die Funktion reorder() nutzen, welche die kategorielle Variable (erstes Funktionsargument) anhand der Werte einer zweiten Variable sortiert (zweites Funktionsargument), und dies absteigend (decreasing als optionales Funktionsargument).
soziodemographie |>
mutate(ist_verheiratet = if_else(ist_verheiratet == TRUE, "verheiratet", "nicht verheiratet")) |>
ggplot(aes(x = reorder(name, alter, decreasing = TRUE), y = alter, fill = ist_verheiratet)) +
geom_col() +
labs(x = "Person", y = "Alter", fill = "Beziehungsstatus")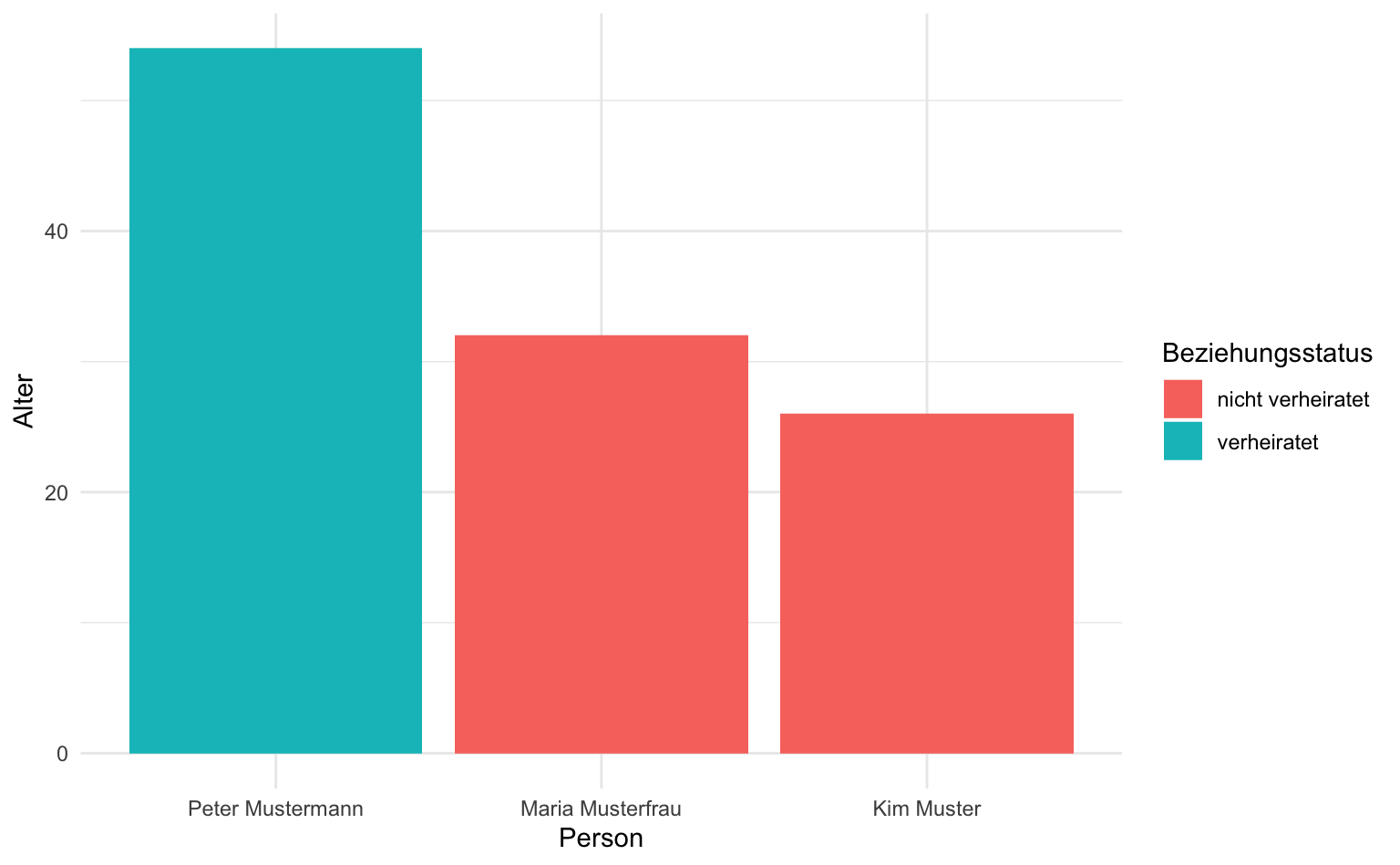
ggplot bestimmt automatisch den Wertebereich für die x- und y-Achse auf Basis der vorliegenden Daten. Zumeist ist dieser Bereich sinnvoll gewählt, aber in manchen Fällen lohnt es sich, diesen anzupassen. Unser Balkendiagramm zur Altersstruktur des Soziodemographie-Datensatzes hat etwa keine weitere Achsenbeschriftung nach dem Wert 40. Deshalb ist es nicht ganz einfach, direkt abzulesen, wie alt Peter Mustermann ist, weil ein oberer Wert als Orientierungspunkt fehlt. Wir können die y-Achse einfach erweitern, indem wir den Wertebereich in ggplot mit der Funktion coord_cartesian(ylim = c(0, 60)) festlegen. Wir können auch den Wertebereich der x-Achse ändern, wenn wir das Funktionsargument xlim nutzen. Beide Funktionsargumente können auch gleichzeitig verwendet werden.
soziodemographie |>
mutate(ist_verheiratet = if_else(ist_verheiratet == TRUE, "verheiratet", "nicht verheiratet")) |>
ggplot(aes(x = reorder(name, alter, decreasing = TRUE), y = alter, fill = ist_verheiratet)) +
geom_col() +
labs(x = "Person", y = "Alter", fill = "Beziehungsstatus") +
coord_cartesian(ylim = c(0, 60))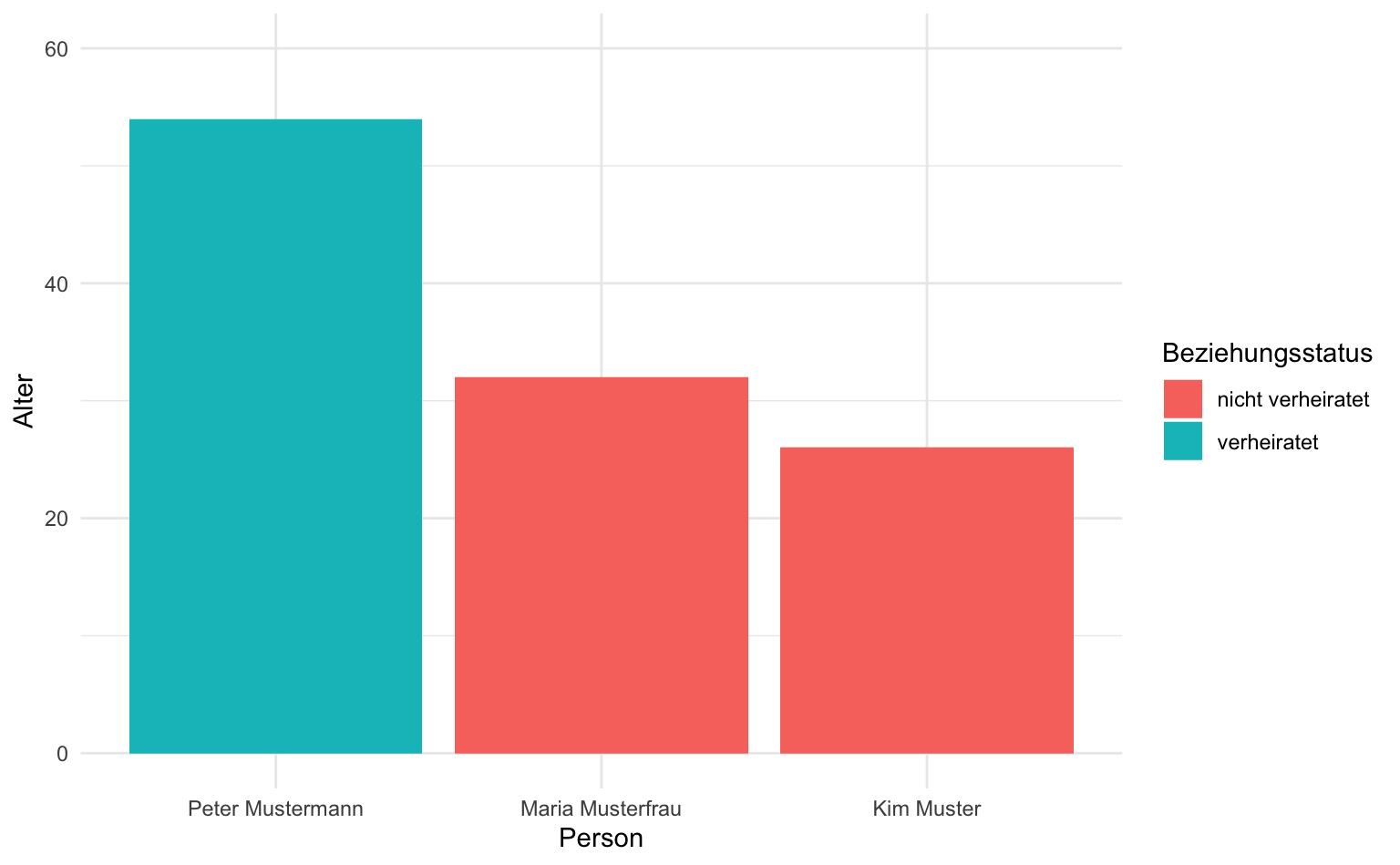
Balkendiagramme werden oft eingesetzt, um Häufigkeitsauszählungen darzustellen. Nachfolgend ein Beispiel anhand der verschiedenen Stimuli des Victim Blaming-Experiments aus dem vorangegangenen Kapitel.
freq_stimulus <- vb |>
count(stimulus_rec)
freq_stimulus# A tibble: 4 × 2
stimulus_rec n
<chr> <int>
1 Extravertiert mit Info 153
2 Extravertiert ohne Info 137
3 Introvertiert mit Info 139
4 Introvertiert ohne Info 157Für die grafische Darstellung benötigen wir wieder nur einige Zeilen.
freq_stimulus |>
ggplot(aes(x = stimulus_rec, y = n)) +
geom_col() +
labs(x = "Versuchsbedingung", y = "Fallzahl n")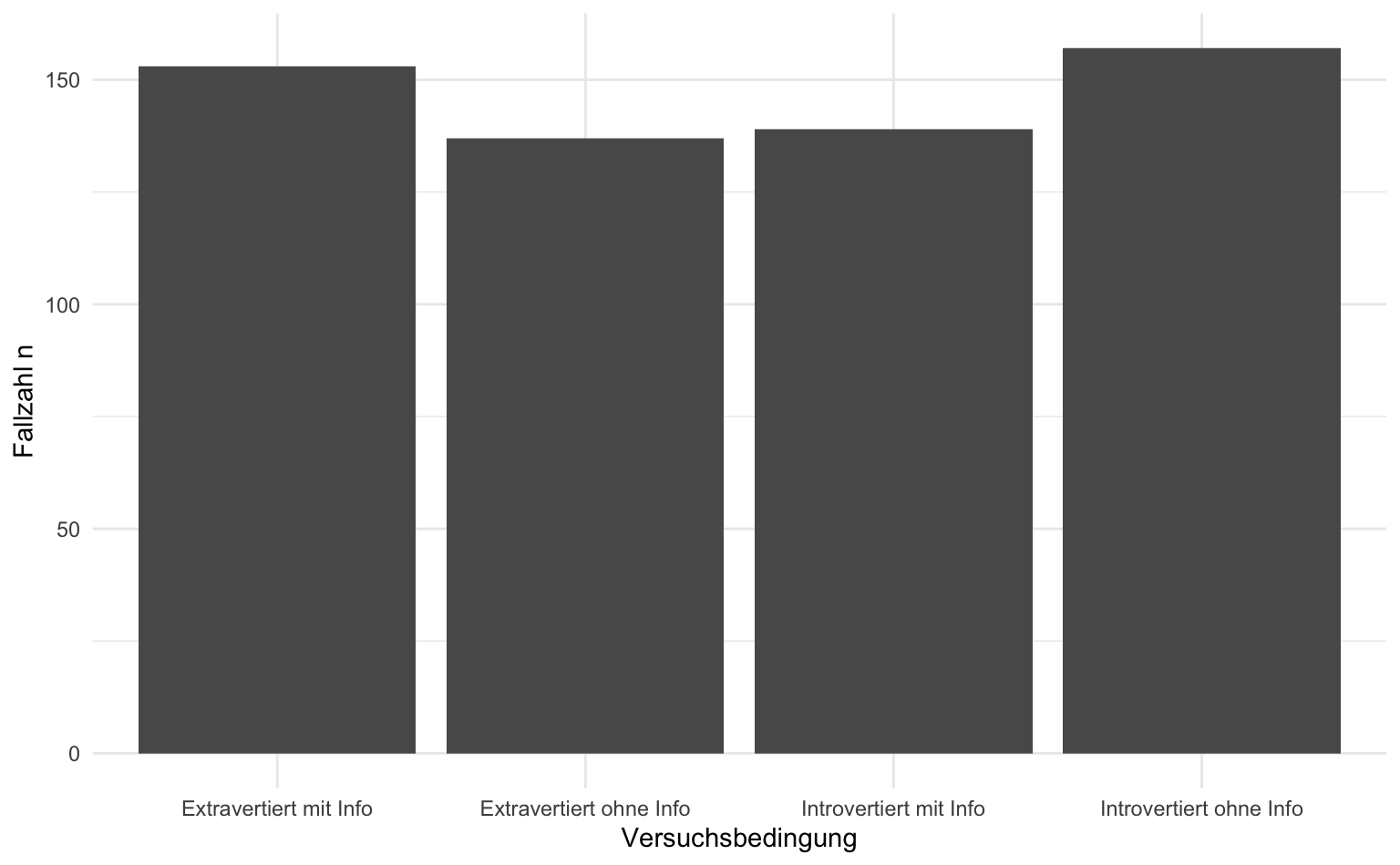
geom_col() und geom_bar()
geom_col() ist nicht zu verwechseln mit der Funktion geom_bar(), welche ebenfalls ein Balkendiagramm erstellt, aber die Anzahl der Fälle für jeden Wert auf der x-Achse berechnet, um die Höhe der Balken zu bestimmen. geom_bar() nutzt im Hintergrund count(), um die Anzahl der Fälle pro Datenpunkt auf der x-Achse zu berechnen. Nutzen wir etwa geom_bar() mit unserem Soziodemographie-Datensatz, dürfen wir in aes keine Variable dem y-Achsenabschnitt zuweisen, weil ggplot() die Höhe (d.h., den Wertebereich auf dem y-Achsenabschnitt) automatisch berechnet.
soziodemographie |>
ggplot(aes(x = name)) +
geom_bar()
Nun sind die Balken gleich hoch für jede Person, da wir für jede Person nur einen einzigen Datenpunkt haben.
7.2 Histogramme
Wollen wir die Häufigkeitsverteilung von Messwerten einer Variable darstellen, können wir mit geom_histogram(), wie es der Name der Funktion bereits verrät, ein Histogramm erstellen. Nachfolgend wollen wir die Häufigkeitsverteilung des Victim Blaming Index mittels eines Histogrammes darstellen. Wir brauchen dafür nur der x-Achse die Variable zuweisen, deren Verteilung uns interessiert.
vb |>
ggplot(aes(x = vb_index)) +
geom_histogram() +
labs(x = "Victim Blaming Index")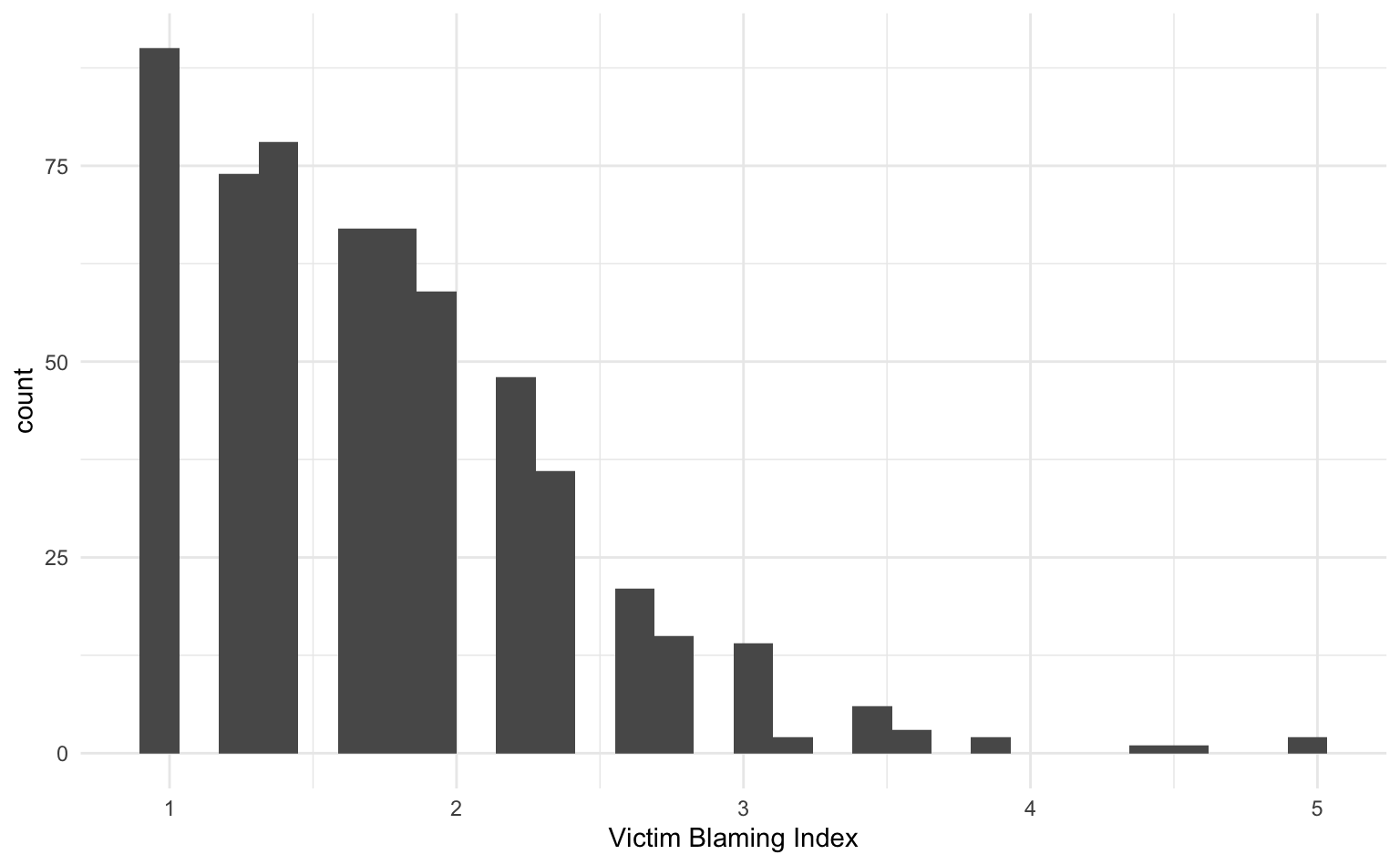
facet_wrap() und gather()
Wir können ebenfalls die Variablen, welche dem Victim Blaiming Index zu Grunde liegen, in einer Grafik darstellen. Dafür benötigen wir zwei zusätzliche Dinge: facet_wrap() (alternativ: facet_grid()) für die Darstellung und Daten im Langformat (engl. long format). Langformat bedeutet, dass einzelne Variablen und deren zugehörige Werte nun untereinander gelistet werden. Aktuell befindet sich der Datensatz im Breitformat (engl. wide format), d.h. jede Variable enthält einen Wert. Nutzen wir gather() sieht den Datensatz nun so aus:
vb |>
select(v_14a:v_14e, vb_index) |>
gather(variablen, wert) |> # variablen und wert sind lediglich die Bezeichnung der neu erzeugten Spalten; die Namen können beliebig gewählt werden
head(., n = 10) # Nur die ersten zehn Werte# A tibble: 10 × 2
variablen wert
<chr> <dbl>
1 v_14a 1
2 v_14a 1
3 v_14a 1
4 v_14a 1
5 v_14a 1
# ℹ 5 more rowsDie Quintessenz von gather() und dem Langformat ist, dass Spalten (Variablen) in Zeilen überführt werden. Da wir ggplot für jeden Achsenabschnitt nur eine Variable übergeben können, wäre es im aktuellen Breitformat unmöglich, alle Variablen des Index grafisch darzustellen. Im Langformat geht dies nun, da die Index-Variablen nun Ausprägungen der Spalte variablen sind und die dazugehörigen Werte nun unter wert stehen. Deshalb empfiehlt sich dieser Workflow immer dann, wenn mehrere Variablen grafisch dargestellt werden sollen.
Mittels facet_wrap(~variable) erhalten wir für jede der Index-Variablen ein separates Histogramm. Wichtig ist, der zugewiesenen Variable eine Tilde ~ voranzustellen, da facet_wrap() eine formula nutzt, wir sie bereits bei map_dfr im Kapitel deskriptive Statistik gesehen haben.
vb |>
select(v_14a:v_14e, vb_index) |>
gather(variablen, wert) |> # gather is mittlerweile ersetzt worden durch pivot_longer(), ist aber noch häufig in Tutorials und Online-Quellen zu finden.
ggplot(aes(x = wert)) +
geom_histogram() +
facet_wrap(~variablen) +
labs(x = "Ausprägung", y = "Häufigkeit")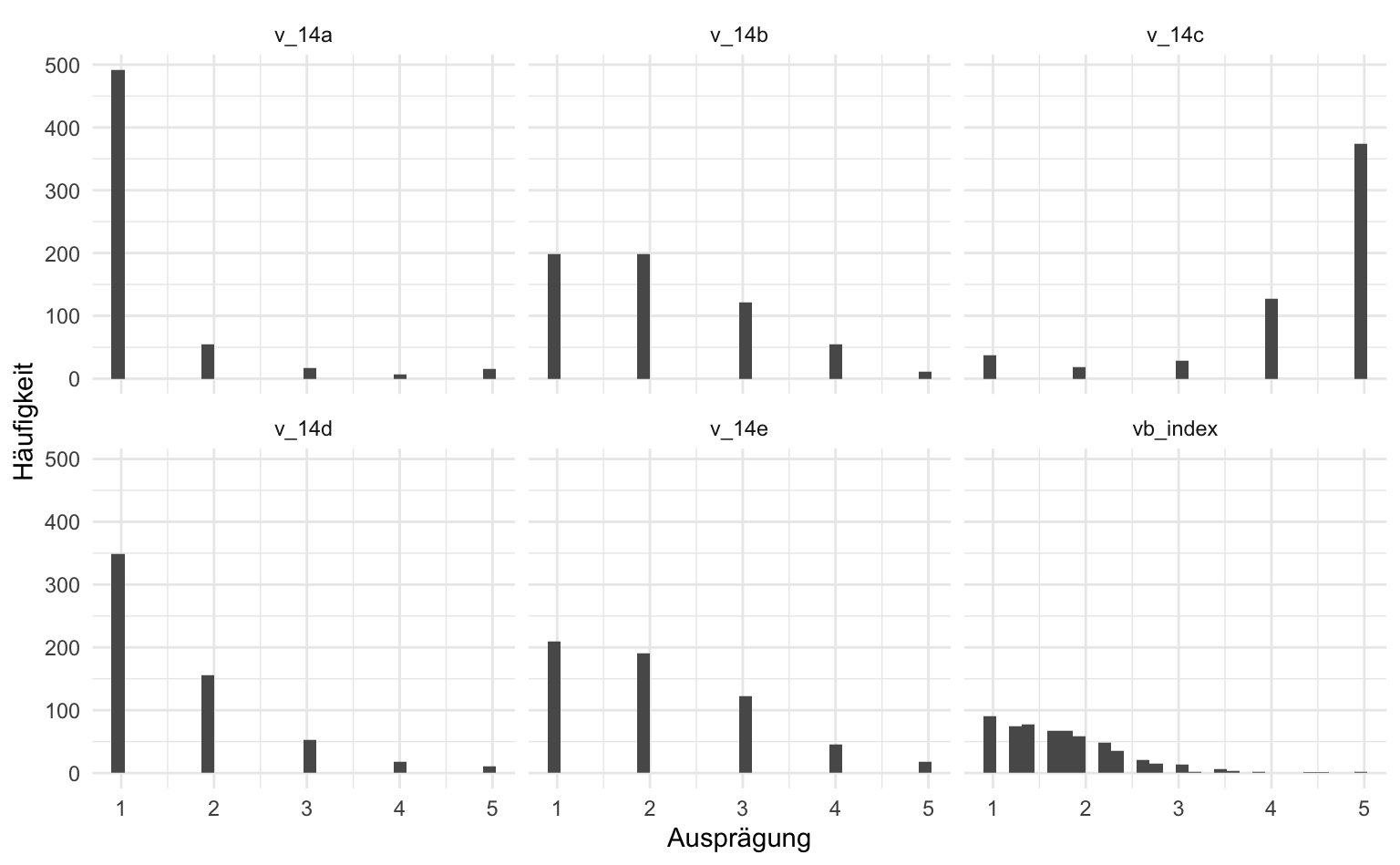
Wollen wir die Überschriften der einzelnen Grafiken (bspw. “vb_index” zu “Index”) ändern, geht dies nicht über labs(), sondern über die Erstellung einer kategoriellen Variable mit den korrekten Bezeichnungen. Alternativ gibt es noch die Möglichkeit, labeller() innerhalb von facet_wrap() zu verwenden.
vb |>
select(v_14a:v_14e, vb_index) |>
gather(variablen, wert) |> # gather is mittlerweile ersetzt worden durch pivot_longer(), ist aber noch häufig in Tutorials und Online-Quellen zu finden.
mutate(variablen = factor(variablen, labels = c("Item 1", "Item 2", "Item 3", "Item 4", "Item 5", "Index"))) |> # Unter labels können wir die Namen der Variablen eintragen
ggplot(aes(x = wert)) +
geom_histogram() +
facet_wrap(~variablen) +
labs(x = "Ausprägung", y = "Häufigkeit")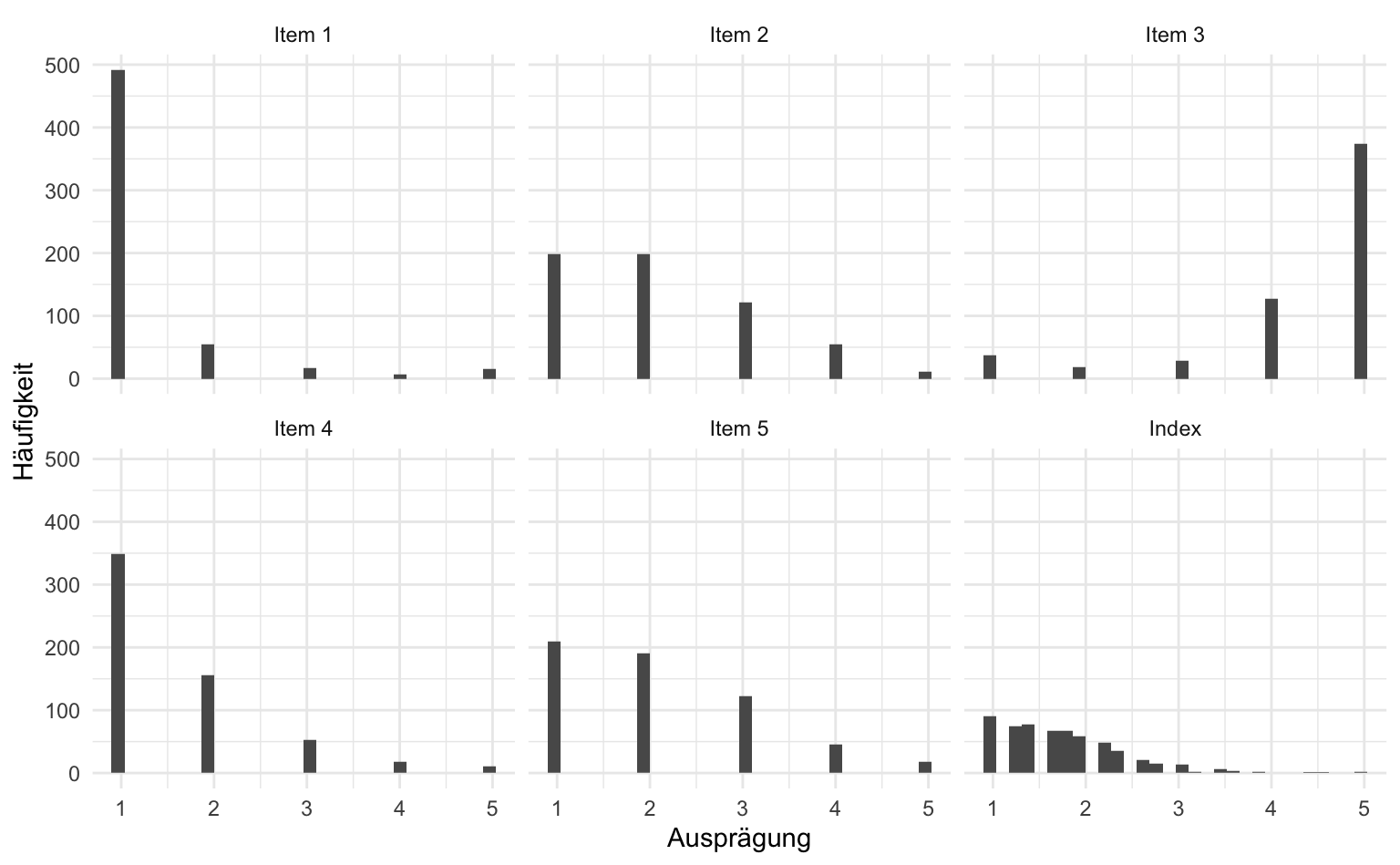
7.3 Streudiagramme
Streudiagramme sind einfach über geom_point darstellbar. Sie eignen sich für (quasi-)metrische Variablen. Wollen wir etwa den Zusammenhang zwischen Sympathie und Attraktivität im Victim Blaming Datensatz darstellen, reichen die folgenden drei Zeilen Code:
vb |>
ggplot(aes(x = v_5j, y = v_5k)) +
geom_point() +
labs(x = "Attraktivität", y = "Sympathie")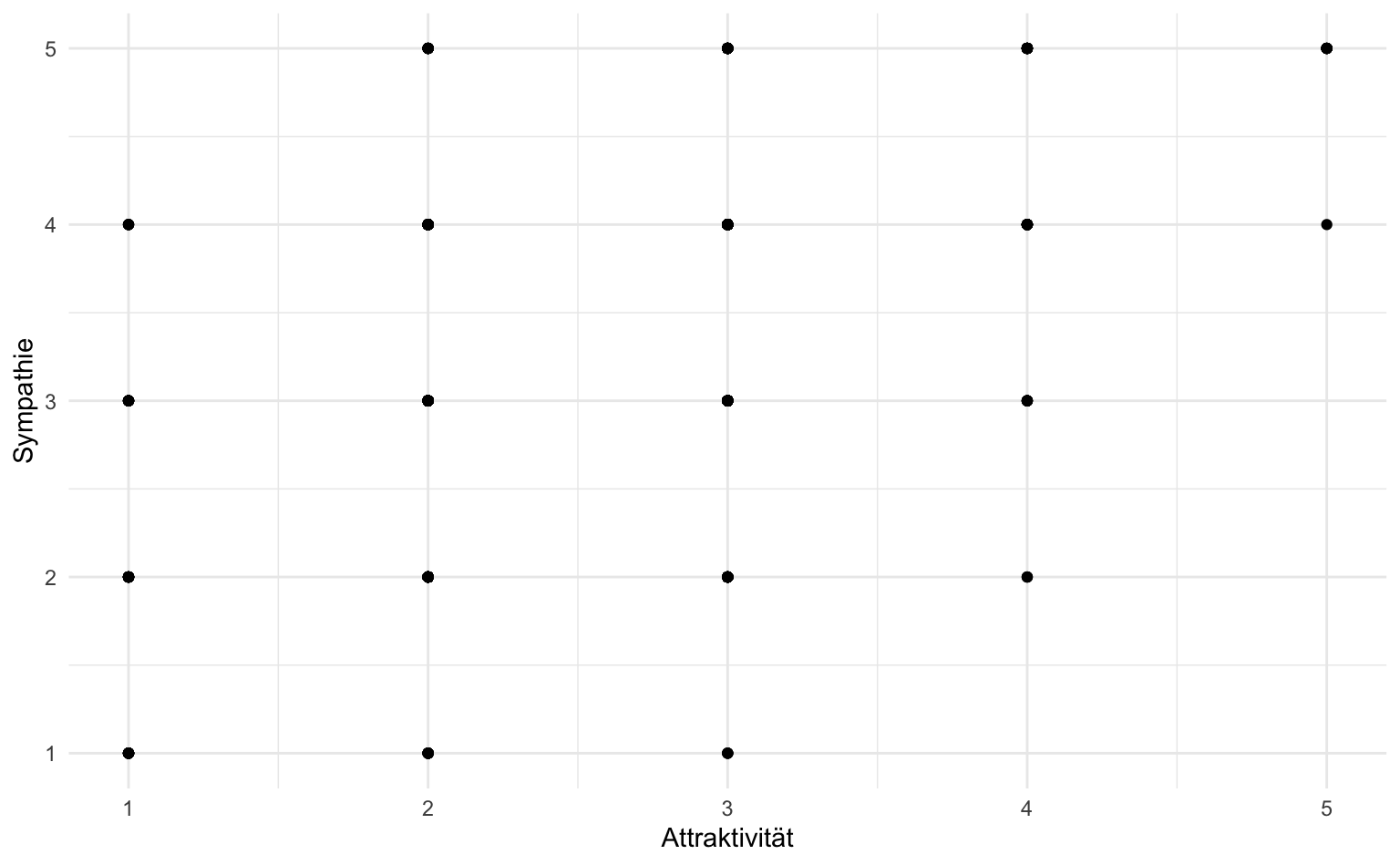
Das Ergebnis sieht noch nicht aus wie ein typisches Streudiagramm, da sich die Datenpunkte überlagern, d.h., dass etwa der Wert im Abschnitt (3.1) für mehrere Beobachtungen steht, diese aber alle als ein einziger Punkt dargestellt werden. Damit die einzelnen Datenpunkte wieder sichtbar werden, können wir eine kleine Zufallszahl zu jedem Datenpunkt hinzufügen. Dafür verwenden wir die Funktion geom_jitter(), welche uns auch die Kontrolle über die Art und Weise wie die Zufallszahl addiert wird bietet. Dafür gibt es die Funktionsargumente width und height, welche einen numerischen Wert erhalten, der, vereinfacht ausgedrückt, bestimmt wie stark die Streuung ist.
vb |>
ggplot(aes(x = v_5j, y = v_5k)) +
geom_jitter(height = 0.5, width = 0.5) +
labs(x = "Attraktivität", y = "Sympathie")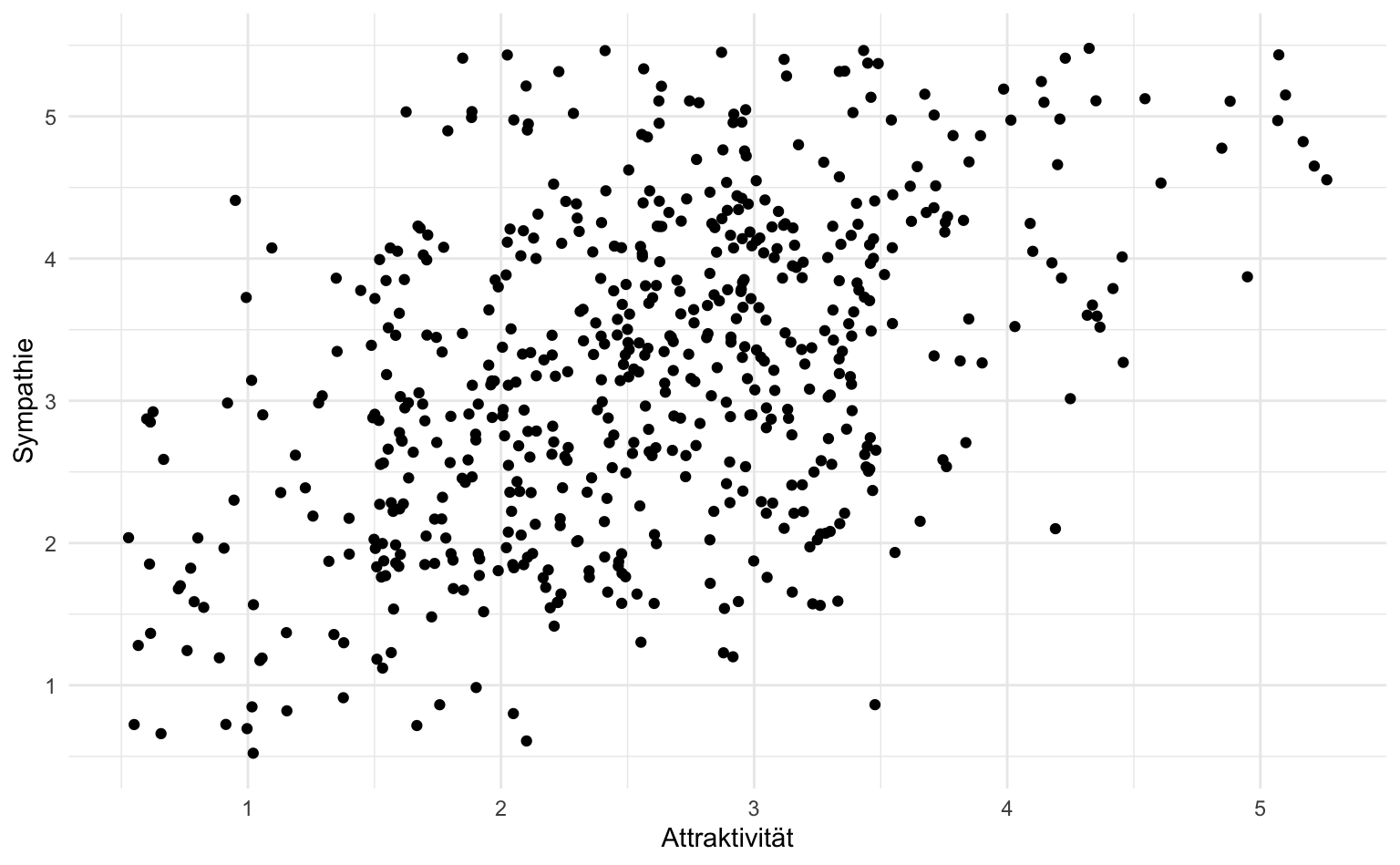
Darüber hinaus können wir wie bereits bei den Balkendiagrammen weitere aesthetics über Variablen vergeben. Beispielsweise das Geschlecht. Hier nutzen wir color, um die Punkte entsprechend des zugehörigen Geschlechts einzufärben. In labs() können wir auch die Legende für die aesthetics color anpassen.
vb |>
ggplot(aes(x = v_5j, y = v_5k, color = v_2)) +
geom_jitter(height = 0.5, width = 0.5) +
labs(x = "Attraktivität", y = "Sympathie", color = "Geschlecht")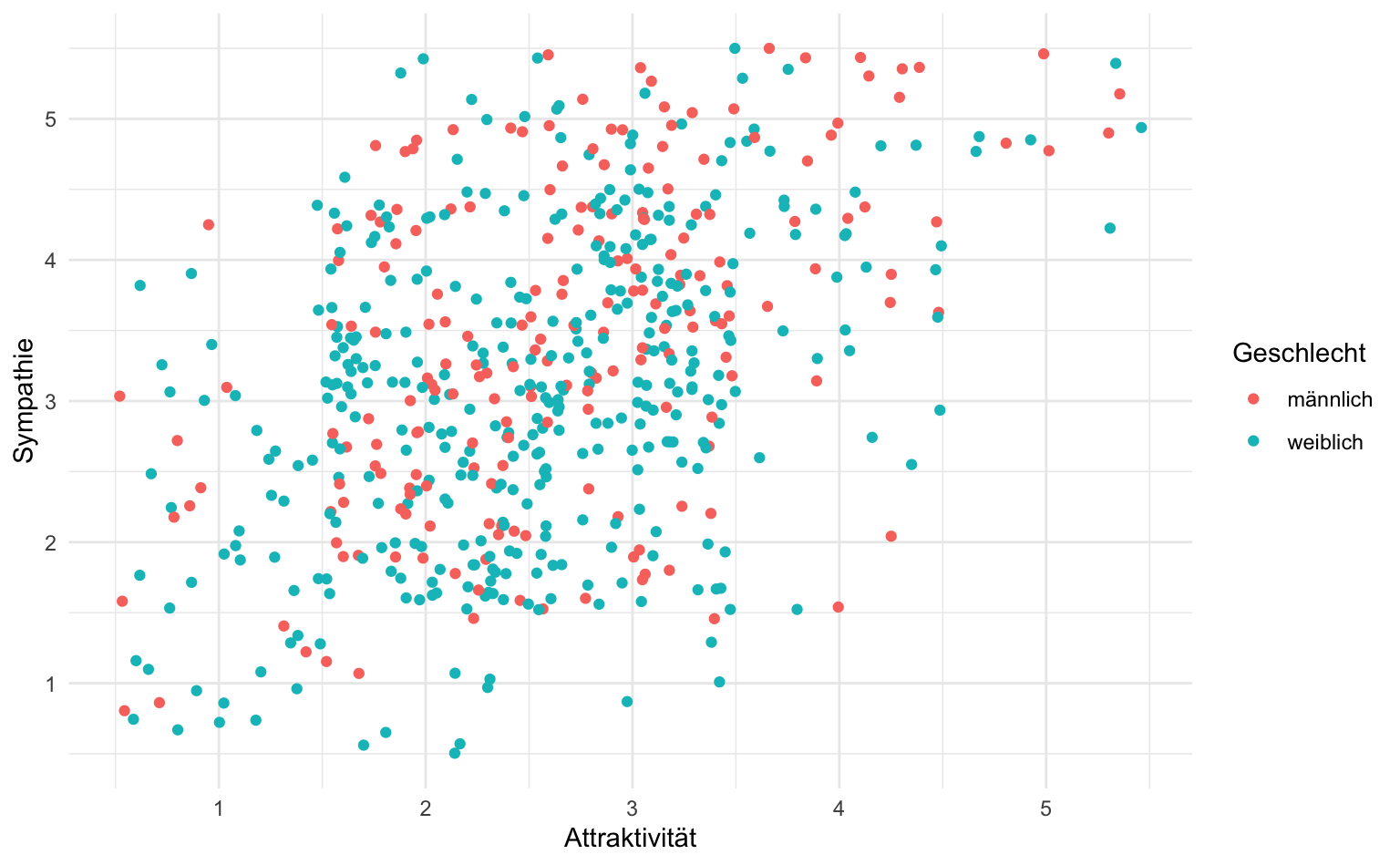
7.4 Liniendiagramme
Liniendiagramme sind besonders geeignet, um Zeitverläufe darzustellen. Wir können diesen Diagrammtyp aber auch dafür verwenden, um Durchschnittswerte über verschiedene Kategorien oder Gruppen zu vergleichen. Nachfolgend berechnen wir für die verschiedenen Altersgruppen den durchschnittlichen Wert des Victim Blaming-Index.
avg_vb <- vb |>
group_by(v_1) |>
summarise(mean_vb = mean(vb_index))
avg_vb# A tibble: 7 × 2
v_1 mean_vb
<dbl> <dbl>
1 16 1.97
2 17 1.87
3 18 1.74
4 19 1.82
5 20 1.75
# ℹ 2 more rowsDie Umsetzung in ggplot ist dann eher einfach. Wir benötigen lediglich geom_line().
avg_vb |>
ggplot(aes(x = v_1, y = mean_vb)) +
geom_line() +
labs(x = "Alter", y = "VB Index (Durchschnitt)")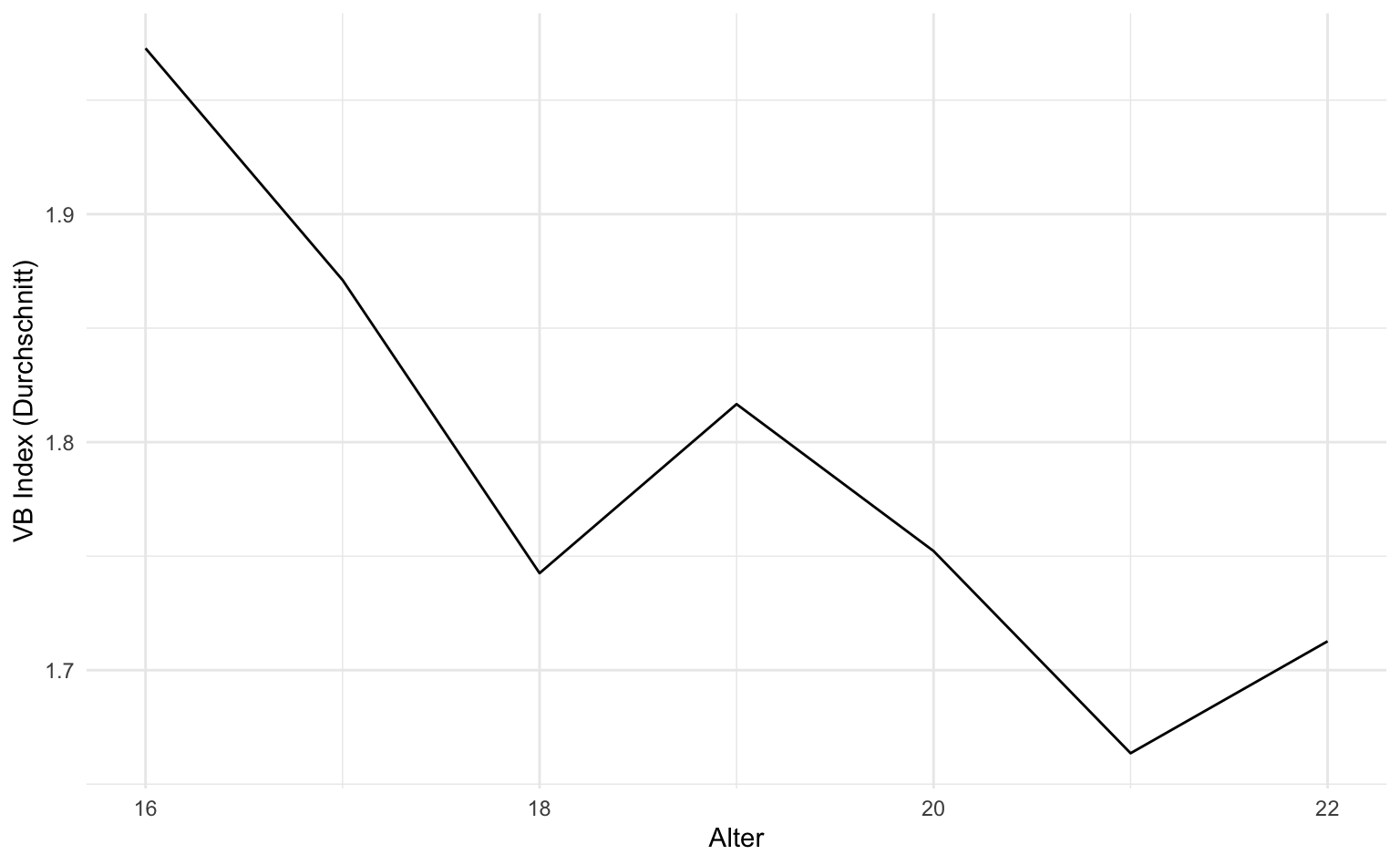
Meist ist es eine gute Idee, auch die Datenpunkte mit geom_point() hinzuzufügen.
avg_vb |>
ggplot(aes(x = v_1, y = mean_vb)) +
geom_line() +
geom_point() +
labs(x = "Alter", y = "VB Index (Durchschnitt)")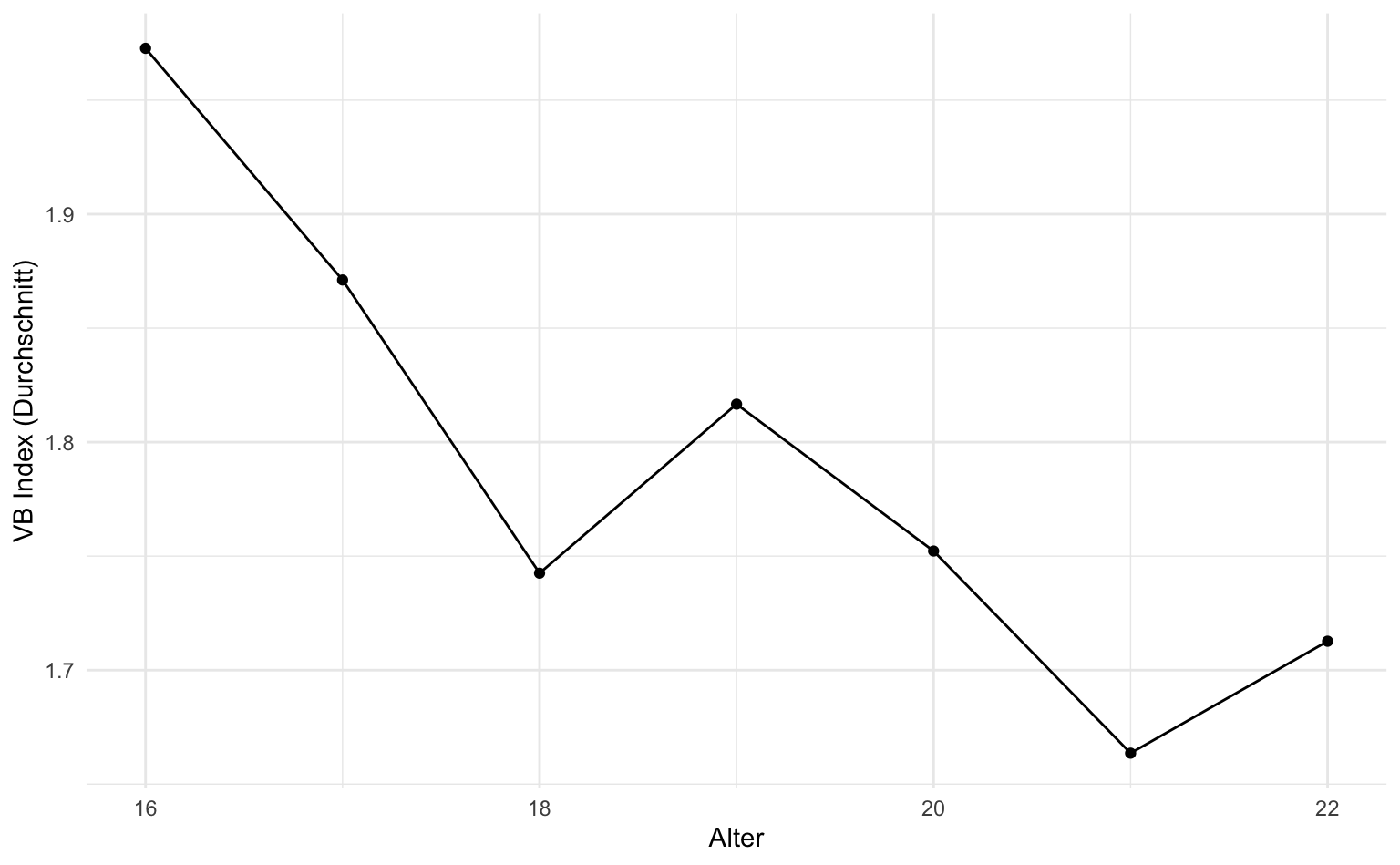
7.5 Glossar
| Funktion | Definition |
|---|---|
| aes() | Bestimmt, welche Variablen zu welchen Dimensionen der Grafik, etwa Achsenabschnitten (x-Achse, y-Achse), Farben oder Formen zugewiesen werden |
| geom_() | Bestimmt, welche grafische Darstellungsform genutzt wird |
| ggplot() | Erstellen von Grafiken |
| labs() | Ermöglicht die Beschriftung der Achsenabschnitte etc. |
7.6 Hausaufgabe
Für die Hausaufgabe analysieren wir den Datensatz gewohnheiten.xlsx.
- Stellen Sie das Alter der Befragten (
p_3) als Histogram dar. - Berechnen Sie die Anzahl der Befragten aus NRW versus allen anderen Bundesländern (
p_5). Visualisieren Sie das Ergebnis. - Lässt sich grafisch ein Zusammenhang zwischen der Tablet- (
i1_tablet) und Computernutzung (i1_computer) feststellen? (mit Antwortsatz)
Für alle Aufgaben gilt:
Geben Sie als Kommentar (mit # beginnend) an, welche Frage Sie bearbeiten, darunter folgt der zugehörige Code.
Die Antwortsätze folgen darunter, ebenfalls als Kommentar (mit # beginnend).